主成分分析法-简单人脸识别(一)
一)主成分分析法
主成分分析法,即PCA算法,直观上来讲就是一种降维方法,例如某件事可能受到好多个因素的影响,假如有ABCDEFG这7个因素,但是呢其中有ABC三个因素对事件的影响基本上是相同的,那么就可以把ABC三个因素用其中的一个因素代替,或者把ABC组合一下用一个全新的因素H来代替,这样因素就降为了4个,实现了降维的过程。
主成分分析最大的好处就是降维,使得数据的处理更容易,速度更快。对于高维数据(超过3维),想观察数据间的结构关系是不可能的,要是三维的或者以下的话还可以,你可以在坐标轴上画出来来观察这些数据之间有什么关系,但是高维就不行了,这个时候就可以用PCA方法进行降维处理成3维或者3维以下,再来观察就可以了。
OK,原理部分牛人们都介绍过了,这里贴几个比较好的介绍:
关于降维:http://blog.csdn.net/jwh_bupt/article/details/8935219
算法原理:
特征脸(Eigenface)理论基础-PCA(主成分分析法)
http://blog.csdn.net/smartempire/article/details/22938315
人脸识别经典算法一:特征脸方法(Eigenface)
人脸识别必读的N篇文章
http://blog.csdn.net/liulianfanjianshi/article/details/9147157
http://blog.csdn.net/miscclp/article/details/7480261
还有很多相关的介绍,作为一个刚过来的新手,想一下子理解还是有点困难,不过慢慢看总还是能看懂的。
二)部分matlab下介绍PCA
为了直观介绍下认识的pca而不去介绍稍微有点晦涩的算法原理,这里给出一个例子吧。现在假设有一组样本点,先给出样本吧,例如随便假设有5个点:
X1 = [1,2];x2 = [2,1];x3 = [3,3];x4 = [3,6];x5 = [6,3];连接起来写在一个矩阵里面就是样本集合:x = [1 2;2 1;3 3;3 6;6 3];
注意了样本的格式,每一行代表一个样本,列表示的是样本的个数,这里可以看到,样本的维度是2,有5个样本,在matlab下画出样本点如下:
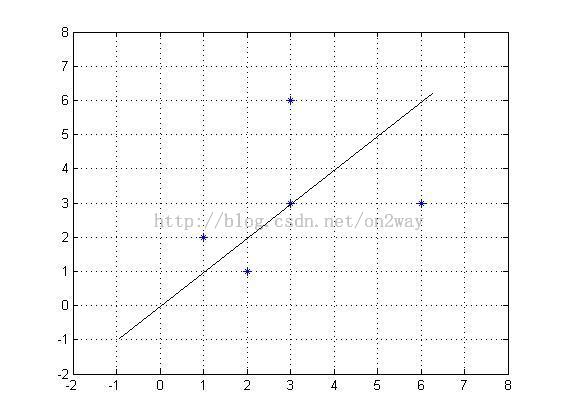
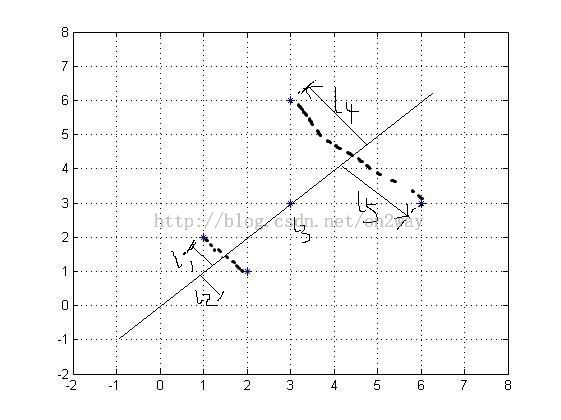
从图中可以看到点的分布,这是在二维下的分布,那么现在我要用一维数据怎么比较好的表示这个二维数据了?这个时候我们需要找到一个方向,让这些点在这个方向上投影,就可以把这些点都投影到一维上了,但是往那个方向上投影?
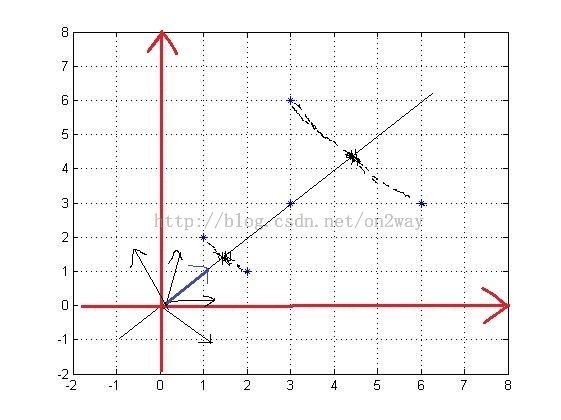
上图显示投影方向很多,但是直观的看到,当投影方向是蓝色的的时候,投影下来最好,样本间的差别最大,才能最好的用该投影方向的数据表示原来的样本。为什么会有这个感觉呢?这就自然联想到了求出这个向量的理论原理上来了。
推导这个原理的方法很多,但是我看好多基本上是用的两种方式(所以方式的结论是一样的)
方式一:投影到低维度下是的样本间距离最大
这里简单画下如下所示:
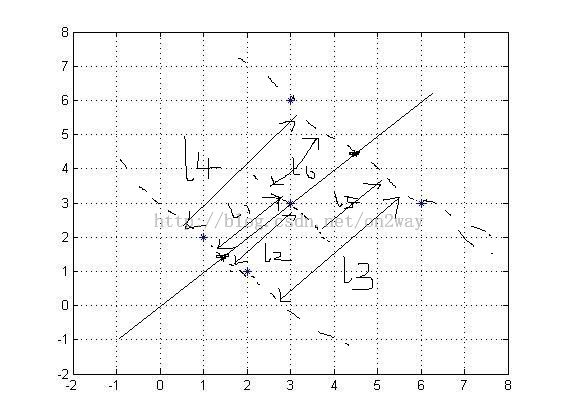
最终的目的就是使得投影的样本每两两之间距离和最大。
这里假设投影向为u,每个样本为x,那么一个样本点在一个向量上的投影长度为多少呢?就是x*u,要注意的是必须一个是行向量,一个是列向量,这样相乘的结果才是一个标量。比如点x(2,1),这里假设向量方向为u(0.707,0.707)(可以直观看出,先用结果了,已经单位化u了),那么x在u方向上的大小是多少?就是 (2,1)*(0.707,0.707)T,为 2.1213。其他点同理求。
那么在不知道u的情况下怎么求它呢?先假设u,那么整个求取的数学表达式就是:![]()
中间那部分可以看出成样本协方差矩阵。用一些符号整体代换如下:
这样λ就是Е的特征值了,u为特征向量。最佳投影直线就是在λ取得最大时的特征向量,其次是第二大的特征值时的特征向量,等等。
关于特征矩阵特征值与特征向量的意义,看上一个转载博客:
http://blog.csdn.net/on2way/article/details/42150435
那么最后的问题就是找到上述矩阵的特征值与特征向量的过程。
方式二:投影到低维度下是的样本到向量方向上的距离最小--》最小平方误差理论。
还是用图来表示:
这样就是要求所有的L相加之和最小了,这个同样可以用上述数学表达式来表示,只不过这里是求最小问题,但是不变的一点就是最终求的的结果是一样的,最终都是寻找那个矩阵的特征值与特征向量问题。(具体推导就去参考网络上的吧)。
三)matlab处理特征值与特征向量
在求取之前首先要求取该矩阵的协方差,也就是那个X*XT。
协方差matlab有自带函数cov,但是直接用的时候当矩阵较大时很耗时。所以一般看到的程序是人们通常用另一种方式求取。
还是以上述数据:x = [1 2;2 1;3 3;3 6;6 3];
直接求协方差
>> cov(x)
ans =
3.5000 1.0000
1.0000 3.5000
另一种方式步骤是:
(2)每一维上,用(x-u)替换x;
(3)协方差T就是x*xT ;
(当然在第二步后有的数据还要进行将标准化。)
这样按步骤就有:
x = [1 2;2 1;3 3;3 6;6 3];
[m,n] = size(x);%取大小
x_mean = mean(x); %求每列平均值
x_mean_all = repmat(x_mean,m,1);%复制平均值到整个矩阵
Z1 = x - x_mean_all;%相差
T1 = Z1'*Z1;%协方差矩阵(注意这个前后相乘顺序很重要,与样本排法有关)
[V1,D1] = eigs(T1,2);%直接求取特征向量与特征值,并按顺序排好了
%2表示降到的维数,这里还是2维
x_new1 = x*V1; %数据在新维度下的值
这样求的的T为
14 4
4 14
可以看到与cov计算出来的结果差4倍,这是因为cov除了(m-1)也就是4了。
这里也可以得出特征向量V1和D1
>> V1,D1
V1 =
0.7071 -0.7071
0.7071 0.7071
D1 =
18 0
0 10
可以看到当特征值为18时,特征向量为(0.707,0.707),当特征值为10的时候,特征向量为(-0.707,0.707);这里可以看到,第一个特征向量方向不是我们前面假设的那个最佳特征向量吗,第二个特征向量方向是与第一个垂直的方向,也就是特征最不明显的方向。因为原始数据就是两个维度,这里变换的也是两个维度。似乎变换了没什么用。但是一般情况下,数据的维度很高,像下一节介绍基于pca人脸识别时的数据,这个时候找到对应的低维数据就很重要了。
最后在新的维度下的样本点变为
>> x_new1
x_new1 =
2.1213 0.7071
2.1213 -0.7071
4.2426 0
6.3640 2.1213
6.3640 -2.1213
这是什么意思呢?相当于在新坐标系下的坐标吧,比如说第一个点在原来的坐标系下为(2,1),变换后在新的坐标系下为(2.1213,0.7071),不防自己去把坐标系旋转一下,看看第一个点在新坐标系下是不是(2.1213,0.7071)?很明显是的,那么其他点依次类推了。