局部二值模式LBP-简单人脸识别(三)
一)局部二值模式简介
前面介绍过关于主成分分析法的识别方法,这个方法是选取的整幅图像的主成分分量来作为新的特征,从某种意义上说这是一种基于全局特征的方法。但是一般图像识别中,仅仅使用全局特征是不够的,获得的识别率较低,更多的时候,表征一副图像的特征也缺少不了局部特征。那么局部二值模式(LBP)就是这样一种表征局部特征的方法。
介绍性原理的文章很多,这里贴个较好的:
人脸识别经典算法二:LBP方法
http://blog.csdn.net/smartempire/article/details/23249517
研究该算法的过程中还发现了一篇较好的硕士论文:
基于LBP的人脸识别研究_黄非非
想深入了解的可以看看。
一)经典LBP特征提取的程序实现
在介绍实现之前请一定要看上述的那篇博客,那个里面有相关的介绍原理,看了这个原理才能知道算法的实现过程。这里也是介绍经典的矩形3*3领域实现方法。
从上述原理可以知道,要得到图像中的每个像素点的LBP值,必须和它的领域有关,所以它的四周必须得有像素点,这就出现了一个问题,对于一个图像边缘像素点来说怎么办?它是边缘点,那么必定存在着它的3*3领域内的某几个点超出图像之外,也就是没有像素值,这样会出现错误的,那么一个解决办法就是对原图像进行像素扩展,也就是把原图像的四周向外扩展一下,像素点的灰度扩展成多少?可以是把边界点的像素复制过去就可以了(当然还有其他方法),知道图像滤波的可能会知道,在滤波算法中也存在着边界点的处理过程,本质上方法是一样的。
考虑到是3*3的矩形领域,那么四周边界点只需要向外扩展一行或者一列就行了。如果矩形框改变大小,那么向外扩展的大小也改变。简单的扩展描述过程如下:
把相应的位置复制到新的扩展图中就可以了。
从原理中看到某个像素点的LBP值得计算公式可以简单描述为:
其中,2^p的系数可以用矩阵代替:C = [1,2,4;128,0,8;64,32,16];
求和可以用矩阵的点乘来代替并求和。矩阵点乘就是矩阵对应位置与对应位置相乘,和矩阵直接相乘还是有很大的区别。
有了上述分析,程序可以写成如下:
%--------------函数说明-------------
%-----LBP:Local Binary Patterns,局部二值模式
%-----输入:img原始灰度图像:注意图片为double型
%-----输出:该图像的的LBP特征
%-----------------------------------
function LBP = Lbp_Img(img)
%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[m,n] = size(img);%取大小
r = 1;
img_extend = zeros(m+2*r,n+2*r);%规定扩展后的矩阵大小并赋值0
img_extend(r+1:m+r,r+1:n+r) = img;%中间部分复制
img_extend(1:r,r+1:n+r) = img(1:r,1:n);%上扩展
img_extend(1:m+r,n+r+1:n+2*r) = img_extend(1:m+r,n+1:n+r);%右扩展
img_extend(m+r+1:m+2*r,r+1:n+2*r) = img_extend(m+1:m+r,r+1:n+2*r);%下扩展
img_extend(1:m+2*r,1:r) = img_extend(1:m+2*r,r+1:r+1:2*r);%左扩展
%%
C = [1,2,4;128,0,8;64,32,16]; %矩阵点乘的权值矩阵
LBP = zeros(m,n);
for i=1:m %对所有的像素点
for j=1:n
temp = img(i,j); %取得该点像素值--也就是中心值
temp_mat = ones(3)*temp; %检测得邻域矩阵3*3
temp_ext = img_extend(i+r-1:i+r+1,j+r-1:j+r+1);%取得邻域矩阵像素点
temp_mean = temp_ext - temp_mat; %相差
temp_mean(find(temp_mean>=0)) = 1; %判断,置0与1
temp_mean(find(temp_mean<0)) = 0;
LBP(i,j) = sum(sum(C.*temp_mean)); %点乘并求和返回LBP
end
end
二):样本图片的LBP提取与直方图显示:
现在对一副图像进行提取整个图像的LBP,很显然一幅图像的LBP必定是与原图像相同大小的矩阵才对。现在我们随意找来一副图像进行提取LBP:
首先转化成灰度图像,并进行double型转换,最后直接运行
LBP = Lbp_Img(img);imshow(LBP,[])
如下(注意imshow函数在显示的时候加上[],使其自适应显示,不然显示不出来这个图):

LBP算法的一大优点就是对光照具有较强的鲁棒性,现在人为用matlab改变一下样本的原始亮度,再显示他们的LBP如下所示:

可以看到在亮度不同的条件下他们的LBP基本上没有多大变化。
那么怎么去进行后续处理呢?一个很重要的处理方法就是对LBP进行灰度直方图处理,在直方图的基础上进一步处理。
对上述得到的LBP,matlab本身自带直方图统计与显示函数hist,但是它只能处理一行或者一列的数据,所以对LBP这种矩阵首先得进行处理成一行再来运用,这里我们又可以运用reshape函数了。处理与显示如下:
>> [m,n] = size(LBP);
data = reshape(LBP,1,m*n);
hist(data,255);
[nel,cen] = hist(data,255);
统计直方图如下所示:
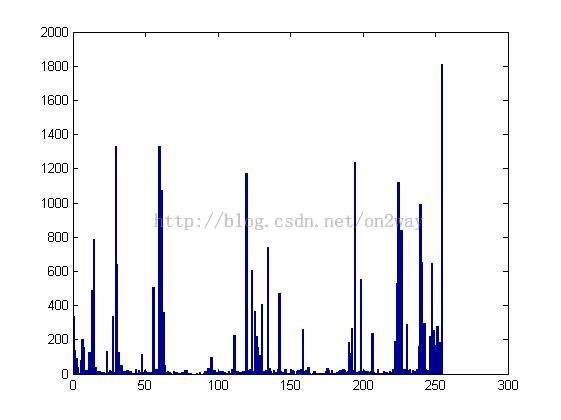
还有一个我们关心的数字就是上述的nel,这是每个像素点的LBP中的总统计个数,而cen是中心点,其实就是1~255(所有灰度值)。nel这个1*n的数据在后面的处理时至关重要。

