Python下opencv使用笔记(三)(图像的几何变换)
- 写在之前
二维与三维图像的几何变换在计算机图形学上有重要的应用,包括现在的许多图像界面的切换、二维与三维游戏画面控制等等都涉及到图像几何变换,就比如说在三维游戏中,控制角色三维移动的时候,画面是要跟着移动的,那么怎么移动,怎么让上一时刻的画面移动到这一时刻,这都是根据了你的移动量,然后找到三维坐标之间的对应关系,用这一时刻的坐标替换到上一时刻的坐标像素值实现图像的切换。 - 图像的几何变换主要包括:平移、扩大与缩小、旋转、仿射、透视等等。图像变换是建立在矩阵运算基础上的,通过矩阵运算可以很快的找到对应关系。理解变换的原理需要理解变换的构造方法以及矩阵的运算方法,曾经写过matlab下的简单图像变换原理,里面有最基础的构造原理可以看看:
matlab之原始处理图像几何变换
(一)图像的平移
下面介绍的图像操作假设你已经知道了为什么需要用矩阵构造才能实现了(上面那个博客有介绍为什么)。那么关于偏移很简单,图像的平移,沿着x方向tx距离,y方向ty距离,那么需要构造移动矩阵:
通过numpy来产生这个矩阵,并将其赋值给仿射函数cv2.warpAffine().
仿射函数cv2.warpAffine()接受三个参数,需要变换的原始图像,移动矩阵M 以及变换的图像大小(这个大小如果不和原始图像大小相同,那么函数会自 动通过插值来调整像素间的关系)。
一个例子如下:
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('flower.jpg')
H = np.float32([[1,0,100],[0,1,50]])
rows,cols = img.shape[:2]
res = cv2.warpAffine(img,H,(rows,cols)) #需要图像、变换矩阵、变换后的大小
plt.subplot(121)
plt.imshow(img)
plt.subplot(122)
plt.imshow(res)(二)图像的扩大与缩小
图像的扩大与缩小有专门的一个函数,cv2.resize(),那么关于伸缩需要确定的就是缩放比例,可以是x与y方向相同倍数,也可以单独设置x与y的缩放比例。另外一个就是在缩放以后图像必然就会变化,这就又涉及到一个插值问题。那么这个函数中,缩放有几种不同的插值(interpolation)方法,在缩小时推荐cv2.INTER_ARER,扩大是推荐cv2.INTER_CUBIC和cv2.INTER_LINEAR。默认都是cv2.INTER_LINEAR,比如:
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('flower.jpg')
# 插值:interpolation
# None本应该是放图像大小的位置的,后面设置了缩放比例,
#所有就不要了
res1 = cv2.resize(img,None,fx=2,fy=2,interpolation=cv2.INTER_CUBIC)
#直接规定缩放大小,这个时候就不需要缩放因子
height,width = img.shape[:2]
res2 = cv2.resize(img,(2*width,2*height),interpolation=cv2.INTER_CUBIC)
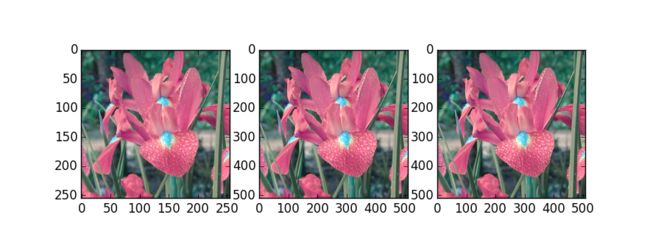
plt.subplot(131)
plt.imshow(img)
plt.subplot(132)
plt.imshow(res1)
plt.subplot(133)
plt.imshow(res2)(三)图像的旋转
图像的旋转矩阵一般为:
但是单纯的这个矩阵是在原点处进行变换的,为了能够在任意位置进行旋转变换,opencv采用了另一种方式:
为了构造这个矩阵,opencv提供了一个函数:
cv2.getRotationMatrix2D(),这个函数需要三个参数,旋转中心,旋转角度,旋转后图像的缩放比例,比如下例:
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('flower.jpg')
rows,cols = img.shape[:2]
#第一个参数旋转中心,第二个参数旋转角度,第三个参数:缩放比例
M = cv2.getRotationMatrix2D((cols/2,rows/2),45,1)
#第三个参数:变换后的图像大小
res = cv2.warpAffine(img,M,(rows,cols))
plt.subplot(121)
plt.imshow(img)
plt.subplot(122)
plt.imshow(res)(四)图像的仿射
图像的旋转加上拉升就是图像仿射变换,仿射变化也是需要一个M矩阵就可以,但是由于仿射变换比较复杂,一般直接找很难找到这个矩阵,opencv提供了根据变换前后三个点的对应关系来自动求解M。这个函数是
M=cv2.getAffineTransform(pos1,pos2),其中两个位置就是变换前后的对应位置关系。输 出的就是仿射矩阵M。然后在使用函数cv2.warpAffine()。形象化的图如下(引用参考的)
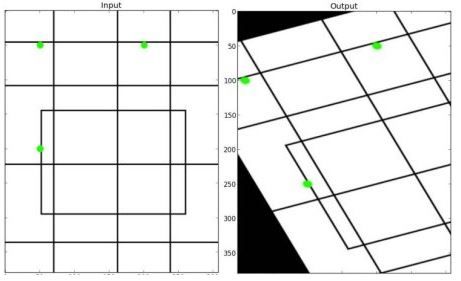
一个例子比如:
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('flower.jpg')
rows,cols = img.shape[:2]
pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[10,100],[200,50],[100,250]])
M = cv2.getAffineTransform(pts1,pts2)
#第三个参数:变换后的图像大小
res = cv2.warpAffine(img,M,(rows,cols))
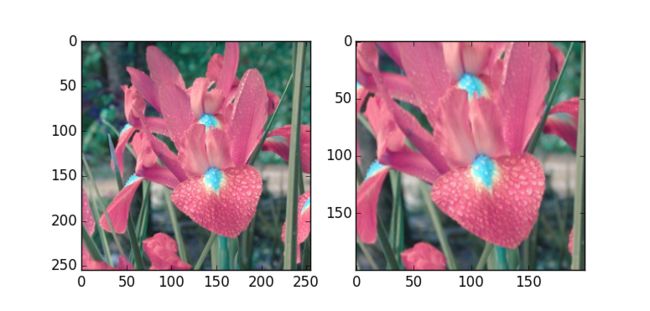
plt.subplot(121)
plt.imshow(img)
plt.subplot(122)
plt.imshow(res)(五)图像的透射
透视需要的是一个3*3的矩阵,同理opencv在构造这个矩阵的时候还是采用一种点对应的关系来通过函数自己寻找的,因为我们自己很难计算出来。这个函数是M = cv2.getPerspectiveTransform(pts1,pts2),其中pts需要变换前后的4个点对应位置。得到M后在通过函数cv2.warpPerspective(img,M,(200,200))进行。形象化的图如下(引用参考的)
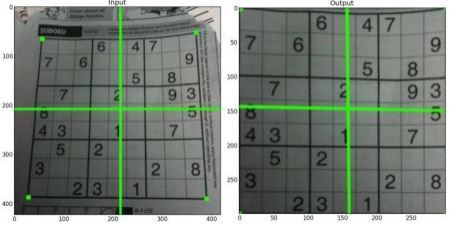
一个例子如下:
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('flower.jpg')
rows,cols = img.shape[:2]
pts1 = np.float32([[56,65],[238,52],[28,237],[239,240]])
pts2 = np.float32([[0,0],[200,0],[0,200],[200,200]])
M = cv2.getPerspectiveTransform(pts1,pts2)
res = cv2.warpPerspective(img,M,(200,200))
plt.subplot(121)
plt.imshow(img)
plt.subplot(122)
plt.imshow(res)