九度OJ-题目1521:二叉树的镜像
题目链接地址:
九度OJ-题目1521:二叉树的镜像
题目描述:
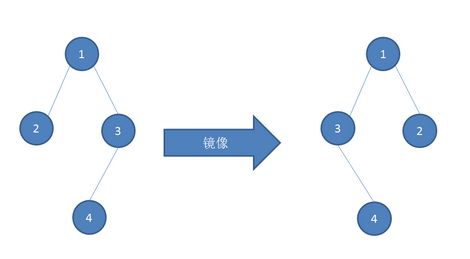
输入一个二叉树,输出其镜像。
输入:
输入可能包含多个测试样例,输入以EOF结束。
对于每个测试案例,输入的第一行为一个整数n(0<=n<=1000,n代表将要输入的二叉树节点的个数(节点从1开始编号)。接下来一行有n个数字,代表第i个二叉树节点的元素的值。接下来有n行,每行有一个字母Ci。
Ci=’d’表示第i个节点有两子孩子,紧接着是左孩子编号和右孩子编号。
Ci=’l’表示第i个节点有一个左孩子,紧接着是左孩子的编号。
Ci=’r’表示第i个节点有一个右孩子,紧接着是右孩子的编号。
Ci=’z’表示第i个节点没有子孩子。
输出:
对应每个测试案例,
按照前序输出其孩子节点的元素值。
若为空输出NULL。
样例输入:
7
8 6 10 5 7 9 11
d 2 3
d 4 5
d 6 7
z
z
z
z
样例输出:
8 10 11 9 6 7 5
解题思路:
解法一 将二叉树的前序遍历顺序改为“中右左”
题目只要求输出二叉树镜像的前序遍历序列,所以只需要在前序遍历二叉树的时候将遍历顺序由原来的“中左右”改为"中右左"即可。
AC代码如下:
// 解法一:仔细分析二叉树的定义,就可以知道将原二叉树所有结点的左右子树进行对换即可得到二叉树的镜像
// 但是题目只要求输出二叉树镜像的前序遍历序列,所以只需要在前序遍历二叉树的时候将遍历顺序改为"中右左"即可
#include<stdio.h>
#define MAX 1001
// 定义二叉树的结点
typedef struct BNode
{
bool isRootNode; // 标记该结点是否为根结点
int data; // 数据域
BNode * lchild; // 左子树
BNode * rchild; // 右子树
}BinaryTreeNode;
BinaryTreeNode biTreeNode[MAX]; // 定义二叉树的结点数组
/**
* 构造有n个结点的二叉树
* @param n 表示二叉树的结点个数
* @return root 返回二叉树的根结点
*/
BinaryTreeNode * createBinaryTree(int n)
{
BinaryTreeNode * root = NULL; // root指向二叉树的根节点
if(0 == n) // 对于空二叉树,直接返回NULL
return root;
char Ci; // Ci代表当前结点的孩子结点情况
int i;
int data; // 二叉树结点的数据域
int leftChild,rightChild; // 二叉树结点的左孩子和右孩子
// 先构造各个结点,初始状态下,每个结点都看成是只有一个结点的二叉树
for(i = 1;i <= n;i++)
{
scanf("%d",&data);
biTreeNode[i].data = data;
biTreeNode[i].lchild = NULL;
biTreeNode[i].rchild = NULL;
biTreeNode[i].isRootNode = true;
}
// 根据各个结点之间的链接关系构造二叉树
for(i = 1;i <= n;i++)
{
char ch;
while((ch = getchar()) != '\n'); //用getchar吃掉前面scanf输入的'\n'和该'\n'之前的多余字符
scanf("%c",&Ci);
switch(Ci)
{
case 'd':
scanf("%d%d",&leftChild,&rightChild);
biTreeNode[i].lchild = &biTreeNode[leftChild];
biTreeNode[i].rchild = &biTreeNode[rightChild];
biTreeNode[leftChild].isRootNode = false; // 表示结点leftChild不是二叉树的根结点
biTreeNode[rightChild].isRootNode = false; // 表示结点rightChild不是二叉树的根结点
break;
case 'l':
scanf("%d",&leftChild);
biTreeNode[i].lchild = &biTreeNode[leftChild];
biTreeNode[i].rchild = NULL;
biTreeNode[leftChild].isRootNode = false; // 表示结点leftChild不是二叉树的根结点
break;
case 'r':
scanf("%d",&rightChild);
biTreeNode[i].lchild = NULL;
biTreeNode[i].rchild = &biTreeNode[rightChild];
biTreeNode[rightChild].isRootNode = false; // 表示结点rightChild不是二叉树的根结点
break;
case 'z':
biTreeNode[i].lchild = NULL;
biTreeNode[i].rchild = NULL;
break;
default:
break;
}//switch
}//for
// 如果某个结点不是任何结点的孩子结点,则该结点就是根结点
for(i = 1;i <= n;i++)
{
if(true == biTreeNode[i].isRootNode)
{
root = &biTreeNode[i]; // root指向根结点
break;
}
}
return root;
}
/**
* 按照"中右左"的顺序前序遍历二叉树就能得到二叉树镜像的前序遍历序列
* @param root 二叉树的根结点
* @return void
*/
void preOrderTraverseImage(BinaryTreeNode * root)
{
if(NULL == root)
return;
printf(" %d",root -> data);
preOrderTraverseImage(root -> rchild);
preOrderTraverseImage(root -> lchild);
}
int main()
{
int n;
BinaryTreeNode * root;
while(EOF != scanf("%d",&n))
{
root = createBinaryTree(n);
if(NULL == root)
{
printf("NULL\n");
}
else
{
printf("%d",root -> data);
preOrderTraverseImage(root -> rchild);
preOrderTraverseImage(root -> lchild);
printf("\n");
}
}
return 0;
}
/**************************************************************
Problem: 1521
User: blueshell
Language: C++
Result: Accepted
Time:0 ms
Memory:1044 kb
****************************************************************/
解法二 将原二叉树所有结点的左右孩子结点进行对换
仔细分析二叉树镜像的定义,可以发现将二叉树中所有结点的左右孩子结点进行对换就可以得到二叉树镜像。
这道题目还有一个地方需要注意:就是在构造二叉树的过程中,第1个结点不一定就是二叉树的根结点,我开始就以为第1个结点就是二叉树的根结点,结果一直Wrong Answer。。。构造二叉树的步骤分为三步:
(1)将各个结点都看成是只有根结点而没有左右孩子的小二叉树,而所需要构造的二叉树则看成是一棵空树;
(2)确定所要构造二叉树中每个结点的左右孩子结点,这个操作会将每个结点都并入到所要构造的二叉树中;
(3)执行完步骤(2)后,再找出没有父结点的结点,该结点就是二叉树的根结点了。
AC代码如下:
// 解法二:仔细分析二叉树的定义,就可以知道将原二叉树所有结点的左右孩子进行对换即可得到二叉树的镜像
#include<stdio.h>
#define MAX 1001
// 定义二叉树的结点
typedef struct BNode
{
bool isRootNode; // 标记该结点是否为根结点
int data; // 数据域
BNode * lchild; // 左子树
BNode * rchild; // 右子树
}BinaryTreeNode;
BinaryTreeNode biTreeNode[MAX]; // 定义二叉树的结点数组
/**
* 构造有n个结点的二叉树
* @param n 表示二叉树的结点个数
* @return root 返回二叉树的根结点
*/
BinaryTreeNode * createBinaryTree(int n)
{
BinaryTreeNode * root = NULL; // root指向二叉树的根节点
if(0 == n) // 对于空二叉树,直接返回NULL
return root;
char Ci; // Ci代表当前结点的孩子结点情况
int i;
int data; // 二叉树结点的数据域
int leftChild,rightChild; // 二叉树结点的左孩子和右孩子
// 先构造各个结点,初始状态下,每个结点都看成是只有一个结点的二叉树
for(i = 1;i <= n;i++)
{
scanf("%d",&data);
biTreeNode[i].data = data;
biTreeNode[i].lchild = NULL;
biTreeNode[i].rchild = NULL;
biTreeNode[i].isRootNode = true;
}
// 根据各个结点之间的链接关系构造二叉树
for(i = 1;i <= n;i++)
{
char ch;
while((ch = getchar()) != '\n'); //用getchar吃掉前面scanf输入的'\n'和该'\n'之前的多余字符
scanf("%c",&Ci);
switch(Ci)
{
case 'd':
scanf("%d%d",&leftChild,&rightChild);
biTreeNode[i].lchild = &biTreeNode[leftChild];
biTreeNode[i].rchild = &biTreeNode[rightChild];
biTreeNode[leftChild].isRootNode = false; // 表示结点leftChild不是二叉树的根结点
biTreeNode[rightChild].isRootNode = false; // 表示结点rightChild不是二叉树的根结点
break;
case 'l':
scanf("%d",&leftChild);
biTreeNode[i].lchild = &biTreeNode[leftChild];
biTreeNode[i].rchild = NULL;
biTreeNode[leftChild].isRootNode = false; // 表示结点leftChild不是二叉树的根结点
break;
case 'r':
scanf("%d",&rightChild);
biTreeNode[i].lchild = NULL;
biTreeNode[i].rchild = &biTreeNode[rightChild];
biTreeNode[rightChild].isRootNode = false; // 表示结点rightChild不是二叉树的根结点
break;
case 'z':
biTreeNode[i].lchild = NULL;
biTreeNode[i].rchild = NULL;
break;
default:
break;
}//switch
}//for
// 如果某个结点不是任何结点的孩子结点,则该结点就是根结点
for(i = 1;i <= n;i++)
{
if(true == biTreeNode[i].isRootNode)
{
root = &biTreeNode[i]; // root指向根结点
break;
}
}
return root;
}
/**
* 将原二叉树所有结点的左右孩子进行对换得到二叉树的镜像
* @param root 二叉树的根结点
* @return void
*/
void makeBinaryTreeImage(BinaryTreeNode * root)
{
if(NULL == root)
return;
BinaryTreeNode * temp;
temp = root -> lchild;
root -> lchild = root -> rchild;
root -> rchild = temp;
makeBinaryTreeImage(root -> lchild);
makeBinaryTreeImage(root -> rchild);
}
/**
* 前序遍历二叉树镜像
* @param root 二叉树的根结点
* @return void
*/
void preOrderTraverseImage(BinaryTreeNode * root)
{
if(NULL == root)
return;
printf(" %d",root -> data);
preOrderTraverseImage(root -> lchild);
preOrderTraverseImage(root -> rchild);
}
int main()
{
int n;
BinaryTreeNode * root;
while(EOF != scanf("%d",&n))
{
root = createBinaryTree(n);
if(NULL == root)
{
printf("NULL\n");
}
else
{
makeBinaryTreeImage(root);
printf("%d",root -> data);
preOrderTraverseImage(root -> lchild);
preOrderTraverseImage(root -> rchild);
printf("\n");
}
}
return 0;
}
/**************************************************************
Problem: 1521
User: blueshell
Language: C++
Result: Accepted
Time:0 ms
Memory:1044 kb
****************************************************************/