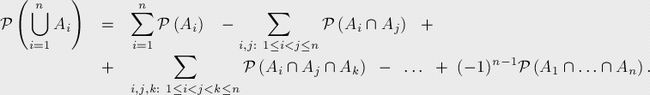[置顶] 容斥原理 专题
http://acm.hdu.edu.cn/showproblem.php?pid=4336
Card Collector
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1410 Accepted Submission(s): 626
Special Judge
Problem Description
In your childhood, do you crazy for collecting the beautiful cards in the snacks? They said that, for example, if you collect all the 108 people in the famous novel Water Margin, you will win an amazing award.
As a smart boy, you notice that to win the award, you must buy much more snacks than it seems to be. To convince your friends not to waste money any more, you should find the expected number of snacks one should buy to collect a full suit of cards.
As a smart boy, you notice that to win the award, you must buy much more snacks than it seems to be. To convince your friends not to waste money any more, you should find the expected number of snacks one should buy to collect a full suit of cards.
Input
The first line of each test case contains one integer N (1 <= N <= 20), indicating the number of different cards you need the collect. The second line contains N numbers p1, p2, ..., pN, (p1 + p2 + ... + pN <= 1), indicating the possibility of each card to appear in a bag of snacks.
Note there is at most one card in a bag of snacks. And it is possible that there is nothing in the bag.
Note there is at most one card in a bag of snacks. And it is possible that there is nothing in the bag.
Output
Output one number for each test case, indicating the expected number of bags to buy to collect all the N different cards.
You will get accepted if the difference between your answer and the standard answer is no more that 10^-4.
You will get accepted if the difference between your answer and the standard answer is no more that 10^-4.
Sample Input
1 0.1 2 0.1 0.4
Sample Output
10.000 10.500
Source
2012 Multi-University Training Contest 4
Recommend
zhoujiaqi2010
关于概率论的原理
设事件
，
代表发生某些事件的概率（即发生其中至少一个事件的概率），则：
#include<iostream>
#include<cstdlib>
#include<stdio.h>
using namespace std;
int n;
double p[25];
double uu;
void dfs(int k,double sum,int cou,int pi)
{
if(cou==k)
{
uu+=1/sum;
return ;
}
for(int i=pi;i<=n;i++)
{
sum+=p[i];
cou++;
dfs(k,sum,cou,i+1);
sum-=p[i];
cou--;
}
return ;
}
int main()
{
while(scanf("%d",&n)!=EOF)
{
double sum=0;
for(int i=1;i<=n;i++)
{
scanf("%lf",&p[i]);sum+=(1/p[i]);
}
for(int i=2;i<=n;i++)
{
uu=0;
dfs(i,0,0,1);
if(i&1) sum+=uu;
else sum-=uu;
}
printf("%lf\n",sum);
}
}
http://acm.hdu.edu.cn/showproblem.php?pid=2461
Rectangles
Time Limit: 5000/4000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1028 Accepted Submission(s): 581
Problem Description
You are developing a software for painting rectangles on the screen. The software supports drawing several rectangles and filling some of them with a color different from the color of the background. You are to implement an important function. The function answer such queries as what is the colored area if a subset of rectangles on the screen are filled.
Input
The input consists of multiple test cases. Each test case starts with a line containing two integers N(1 ≤ N ≤ 20) and M(1 ≤ M ≤ 100000), indicating the number of rectangles on the screen and the number of queries, respectively.
The i-th line of the following N lines contains four integers X1,Y1,X2,Y2 (0 ≤ X1 < X2 ≤ 1000, 0 ≤ Y1 < Y2 ≤ 1000), which indicate that the lower-left and upper-right coordinates of the i-th rectangle are (X1, Y1) and (X2, Y2). Rectangles are numbered from 1 to N.
The last M lines of each test case describe M queries. Each query starts with a integer R(1<=R ≤ N), which is the number of rectangles the query is supposed to fill. The following list of R integers in the same line gives the rectangles the query is supposed to fill, each integer of which will be between 1 and N, inclusive.
The last test case is followed by a line containing two zeros.
The i-th line of the following N lines contains four integers X1,Y1,X2,Y2 (0 ≤ X1 < X2 ≤ 1000, 0 ≤ Y1 < Y2 ≤ 1000), which indicate that the lower-left and upper-right coordinates of the i-th rectangle are (X1, Y1) and (X2, Y2). Rectangles are numbered from 1 to N.
The last M lines of each test case describe M queries. Each query starts with a integer R(1<=R ≤ N), which is the number of rectangles the query is supposed to fill. The following list of R integers in the same line gives the rectangles the query is supposed to fill, each integer of which will be between 1 and N, inclusive.
The last test case is followed by a line containing two zeros.
Output
For each test case, print a line containing the test case number( beginning with 1).
For each query in the input, print a line containing the query number (beginning with 1) followed by the corresponding answer for the query. Print a blank line after the output for each test case.
For each query in the input, print a line containing the query number (beginning with 1) followed by the corresponding answer for the query. Print a blank line after the output for each test case.
Sample Input
2 2 0 0 2 2 1 1 3 3 1 1 2 1 2 2 1 0 1 1 2 2 1 3 2 2 1 2 0 0
Sample Output
Case 1: Query 1: 4 Query 2: 7 Case 2: Query 1: 2
Source
2008 Asia Hefei Regional Contest Online by USTC
Recommend
teddy
题意：给n个矩形，然后每次涂m个矩形，问涂上色的面积是多少。
#include<iostream>
#include<cstdlib>
#include<stdio.h>
#include<algorithm>
using namespace std;
int n,m,num,res;
int a[25];
struct Node
{
int x1,y1,x2,y2;
int s;
}node[25];
bool check(Node x,int u)
{
if(node[u].x1>=x.x2) return 0;
if(x.x1>=node[u].x2) return 0;
if(node[u].y1>=x.y2) return 0;
if(x.y1>=node[u].y2) return 0;
return 1;
}
void solve(Node rec,int id,int k)
{
Node temp;
if(id==num+1) return ;
for(int i=id;i<=num;i++)
{
if(check(rec,a[i]))
{
temp.x1=rec.x1>node[a[i]].x1?rec.x1:node[a[i]].x1;
temp.y1=rec.y1>node[a[i]].y1?rec.y1:node[a[i]].y1;
temp.x2=rec.x2<node[a[i]].x2?rec.x2:node[a[i]].x2;
temp.y2=rec.y2<node[a[i]].y2?rec.y2:node[a[i]].y2;
temp.s=(temp.x2-temp.x1)*(temp.y2-temp.y1);
if(k%2) res+=temp.s;
else res-=temp.s;
solve(temp,i+1,k+1);
}
}
}
int main()
{
int count=1;
while(scanf("%d%d",&n,&m)!=EOF)
{
if(n==0&&m==0) break;
for(int i=1;i<=n;i++)
{
scanf("%d%d%d%d",&node[i].x1,&node[i].y1,&node[i].x2,&node[i].y2);
node[i].s=(node[i].x2-node[i].x1)*(node[i].y2-node[i].y1);
}
printf("Case %d:\n",count++);
for(int i=1;i<=m;i++)
{
scanf("%d",&num);
res=0;
for(int j=1;j<=num;j++)
{
scanf("%d",&a[j]);
res+=node[a[j]].s;
}
for(int j=1;j<=num;j++)
{
solve(node[a[j]],j+1,0);
}
printf("Query %d: ",i);
printf("%d\n",res);
}
puts("");
}
return 0;
}
http://acm.hdu.edu.cn/showproblem.php?pid=1796
How many integers can you find
Time Limit: 12000/5000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 2374 Accepted Submission(s): 665
Problem Description
Now you get a number N, and a M-integers set, you should find out how many integers which are small than N, that they can divided exactly by any integers in the set. For example, N=12, and M-integer set is {2,3}, so there is another set {2,3,4,6,8,9,10}, all the integers of the set can be divided exactly by 2 or 3. As a result, you just output the number 7.
Input
There are a lot of cases. For each case, the first line contains two integers N and M. The follow line contains the M integers, and all of them are different from each other. 0<N<2^31,0<M<=10, and the M integer are non-negative and won’t exceed 20.
Output
For each case, output the number.
Sample Input
12 2
2 3
Sample Output
7
Author
wangye
Source
2008 “Insigma International Cup” Zhejiang Collegiate Programming Contest - Warm Up（4）
Recommend
wangye
题意：给你一个数n和一个包含m个数的集合，让你求小于n的有多少个数能整除这m个数中的任意一个。
n以内能整除m个数中一个数的个数的和-n以内能整除m个数中两个数的个数的和+n以内能整除m个数中三个数的和……
#include<iostream>
#include<cstdlib>
#include<stdio.h>
#define ll __int64
using namespace std;
int a[15];
ll res,n;
int m;
int gcd(int x,int y)
{
if(y==0) return x;
return gcd(y,x%y);
}
int lcm(int x,int y)
{
return x/gcd(x,y)*y;
}
void dfs(int now,int step,int k)
{
if(step==m+1) return ;
for(int i=step;i<=m;i++)
{
if(a[i]!=0)
{
int temp=lcm(now,a[i]);//应该是最小公倍数，而不是乘积，一开始nc了~
int ans=n/temp;
if(n%temp==0) ans--;
if(k%2) res+=ans;
else res-=ans;
dfs(temp,i+1,k+1);
}
}
}
int main()
{
while(scanf("%I64d%d",&n,&m)!=EOF)
{
res=0;
for(int i=1;i<=m;i++)
{
scanf("%d",&a[i]);
if(a[i]!=0)
{
int num=n/a[i];
if(n%a[i]==0) num--;
res+=num;
}
}
for(int i=1;i<=m;i++)
{
if(a[i]!=0)
dfs(a[i],i+1,0);
}
printf("%I64d\n",res);
}
}
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3556
Give a set S, |S| = n, then how many ordered set group (S1, S2, ..., Sk) satisfies S1 ∩ S2 ∩ ... ∩ Sk = ∅. (Si is a subset of S, (1 <=i <=k))
Input
The input contains multiple cases, each case have 2 integers in one line representn andk(1 <=k <=n <= 231-1), proceed to the end of the file.
Output
Output the total number mod 1000000007.
Sample Input
1 1 2 2
Sample Output
1 9
个数为n的集合的子集有2^n个，从中选出K个使得他们的交集为空的个数。
由于集合可以重复被选，所以总的数目是2^(kn)
然后选中的集合都包含x这个数的数目是c(n,1)*2^(n-1)k
选中的集合包含x1,x2的数目是c(n,2)*2^(n-2)k
……
所以满足的集合的个数res=2^kn-c(n,1)*2^(n-1)k+c(n,2)*2^(n-2)k-……
推出的公式为(2^k-1)^n
#include<iostream>
#include<cstdlib>
#include<stdio.h>
using namespace std;
#define mm 1000000007
typedef long long ll;
ll powermod(ll a,ll b)
{
ll res=1;
while(b)
{
if(b&1)res=(res*a)%mm;//不能写成res*=a%mm~~~~~~~~~
a=a*a;
a%=mm;
b>>=1;
}
return res%mm;
}
int main()
{
ll n,k;
while(scanf("%lld%lld",&n,&k)!=EOF)
{
ll ans=powermod(2,k);
ans--;
ans=powermod(ans,n);
printf("%lld\n",ans);
}
}
http://poj.org/problem?id=1091
跳蚤
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 6620 | Accepted: 1855 |
Description
Z城市居住着很多只跳蚤。在Z城市周六生活频道有一个娱乐节目。一只跳蚤将被请上一个高空钢丝的正中央。钢丝很长，可以看作是无限长。节目主持人会给该跳蚤发一张卡片。卡片上写有N+1个自然数。其中最后一个是M，而前N个数都不超过M，卡片上允许有相同的数字。跳蚤每次可以从卡片上任意选择一个自然数S，然后向左，或向右跳S个单位长度。而他最终的任务是跳到距离他左边一个单位长度的地方，并捡起位于那里的礼物。
比如当N=2，M=18时，持有卡片(10, 15, 18)的跳蚤，就可以完成任务：他可以先向左跳10个单位长度，然后再连向左跳3次，每次15个单位长度，最后再向右连跳3次，每次18个单位长度。而持有卡片(12, 15, 18)的跳蚤，则怎么也不可能跳到距他左边一个单位长度的地方。
当确定N和M后，显然一共有M^N张不同的卡片。现在的问题是，在这所有的卡片中，有多少张可以完成任务。
比如当N=2，M=18时，持有卡片(10, 15, 18)的跳蚤，就可以完成任务：他可以先向左跳10个单位长度，然后再连向左跳3次，每次15个单位长度，最后再向右连跳3次，每次18个单位长度。而持有卡片(12, 15, 18)的跳蚤，则怎么也不可能跳到距他左边一个单位长度的地方。
当确定N和M后，显然一共有M^N张不同的卡片。现在的问题是，在这所有的卡片中，有多少张可以完成任务。
Input
两个整数N和M(N <= 15 , M <= 100000000)。
Output
可以完成任务的卡片数。
Sample Input
2 4
Sample Output
12
Hint
这12张卡片分别是：
(1, 1, 4), (1, 2, 4), (1, 3, 4), (1, 4, 4), (2, 1, 4), (2, 3, 4),
(3, 1, 4), (3, 2, 4), (3, 3, 4), (3, 4, 4), (4, 1, 4), (4, 3, 4)
(1, 1, 4), (1, 2, 4), (1, 3, 4), (1, 4, 4), (2, 1, 4), (2, 3, 4),
(3, 1, 4), (3, 2, 4), (3, 3, 4), (3, 4, 4), (4, 1, 4), (4, 3, 4)
Source
HNOI 2001
题意：n+1个自然数，其中m是确定的，其他n个数都不超过m,有多少种方案使得a1x1+a2x2……+an+1xn+1=1.根据欧几里得，可知题目是要求有多少个这样的序列a1,a2……an+1，他们的最大公约数为1.由于其中一个数确定是m,而其他的数都小于等于m，所以我们只要把m分解质因数，如m=60,那么m分解得 m=2^2*3*5,利用容斥原理，总的可能数是m^n,m以内有2这个质因数的个数是m/2,所以序列包含2这个公因子的种类有(m/2)^n,依此类推……
#include<iostream>
#include<cstdlib>
#include<stdio.h>
#include<math.h>
#define ll __int64
using namespace std;
ll n,m;
ll p[65];
ll a[65];
int cc;
ll ans;
void get()
{
int i;
cc=0;
ll mm=m;
for(i=2;i*i<=mm;i++)
{
if(mm%i==0)
{
p[cc++]=i;
while(mm%i==0)
mm/=i;
}
}
if(mm>1)
p[cc++]=mm;
}
ll quickpower(ll a,ll b)
{
ll res=1;
while(b)
{
if(b&1) res*=a;
a=a*a;
b>>=1;
}
return res;
}
void get_sum(int id,int step,int num)
{
if(step==num)
{
ll uu=m;
for(int i=0;i<step;i++)
uu/=a[i];
ans+=quickpower(uu,n);
return ;
}
for(int i=id;i<cc;i++)
{
a[step]=p[i];
get_sum(i+1,step+1,num);
}
return ;
}
int main()
{
while(scanf("%I64d%I64d",&n,&m)!=EOF)
{
get();
ll res=quickpower(m,n);
for(int i=1;i<=cc;i++)
{
ans=0;
get_sum(0,0,i);
if(i&1) res-=ans;
else res+=ans;
}
printf("%I64d\n",res);
}
}
http://poj.org/problem?id=3904
Sky Code
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 835 | Accepted: 238 |
Description
Stancu likes space travels but he is a poor software developer and will never be able to buy his own spacecraft. That is why he is preparing to steal the spacecraft of Petru. There is only one problem – Petru has locked the spacecraft with a sophisticated cryptosystem based on the ID numbers of the stars from the Milky Way Galaxy. For breaking the system Stancu has to check each subset of four stars such that the only common divisor of their numbers is 1. Nasty, isn’t it? Fortunately, Stancu has succeeded to limit the number of the interesting stars to N but, any way, the possible subsets of four stars can be too many. Help him to find their number and to decide if there is a chance to break the system.
Input
In the input file several test cases are given. For each test case on the first line the number N of interesting stars is given (1 ≤ N ≤ 10000). The second line of the test case contains the list of ID numbers of the interesting stars, separated by spaces. Each ID is a positive integer which is no greater than 10000. The input data terminate with the end of file.
Output
For each test case the program should print one line with the number of subsets with the asked property.
Sample Input
4 2 3 4 5 4 2 4 6 8 7 2 3 4 5 7 6 8
Sample Output
1 0 34
Source
Southeastern European Regional Programming Contest 2008
//这题很久以前做过了，好久没有接触过容斥了，拿来复习复习
//求得是n个数中，有多少组(a,b,c,d)的公约数为1，值得注意的是这四个数不一定两两互质。
//所以我们从它的反面考虑，先求出公约数不为1的个数。
//思路：把每个数素数分解，记录不重复素因子所能组成的因子，把这些因子的总数统计，并且统计每个因子是由多少个素因子组成
//如这n个数中含2的个数为a,含3的个数为b,含6的个数为c,那么公约数大于1的总数为p=c(a,4)+c(b,4)-c(c,4),总的个数为c(n,4)
//用c(n,4)-p即为所求
#include<iostream>
#include<cstdlib>
#include<stdio.h>
#include<memory.h>
using namespace std;
#define maxn 10005
long long count[maxn];
long long num[maxn];
long long p[maxn];
long long prime[maxn];
void init()
{
memset(p,0,sizeof(p));
memset(num,0,sizeof(num));
for(long long i=4;i<maxn;i++)
p[i]=i*(i-1)*(i-2)*(i-3)/24;
}
void solve(long long n)
{
long long tol=0;
for(long long i=2;i*i<=n;i++)
{
if(n%i==0)
{
prime[tol++]=i;
}
while(n%i==0)
n/=i;
}
if(n!=1)
prime[tol++]=n;
for(long long i=1;i<(1<<tol);i++)
{
long long k=1;
long long sum=0;
for(long long j=0;j<tol;j++)
{
if(i&(1<<j))
{
k*=prime[j];
sum++;
}
}
count[k]++;//记录当前因子的个数
num[k]=sum;//记录当前因子是由多少个素因子组成
}
}
int main()
{
init();
long long n;
long long m;
while(scanf("%lld",&n)!=EOF)
{
memset(count,0,sizeof(count));
for(long long i=0;i<n;i++)
{
scanf("%lld",&m);
solve(m);
}
long long ans=0;
for(long long i=0;i<maxn;i++)
{
if(count[i])
{
if(num[i]%2)
{
ans+=p[count[i]];
}
else
ans-=p[count[i]];
}
}
cout<<p[n]-ans<<endl;
}
}