花瓶收集 POJ1632 经典DFS 枚举+暴搜
做这道题的第一个障碍在于读题。刚开始把题目读了三遍,也没搞清楚要求什么。其实可以把shape和decoration看成点,它们之际的对应关系看成边,这样就得到一个图。用A表示shape的集合,B表示decoration的集合。题目要求的就是原图的一个最大子图:使得该子图也可以分为A’和B’两部分,且从A’的每个点出发,到B’的任意点都存在边。
该题的思路:枚举+暴搜。即:枚举K值,对每个k值进行DFS搜索。那么,数据的规模有多大?暴搜是否可行?设最大子图的A’和B’集合各有K个点,则最大子图共有K*K条边。现在原图共有m条边,且m<100。显然,MAX( k ) <= sqrt( 100 ) = 10,也就是说数据规模很小,暴搜可行。
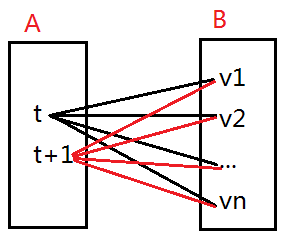
具体的搜索过程:依次检测A集合中的每个点,判断该点是否在A’中。设当前检测的点为t,则存在两种情况:t在A’中,t不在A’。对这两种情况,再分别递归调用DFS。设点t已经在A’中,且v1, v2,…vn分别为集合B中与点t有对应关系的点。根据题目,下一个点t+1也在A’中的条件是:v1, v2,…vn同样也是B中与t+1有对应关系的点。
在具体编程实现的时候,需要存储shape和decoration的对应关系。当然,第一反应是用一个二维数组。但是,仔细想想:要判断t+1的对应点同样也是t的对应点,用位运算&应该更容易,因此可以用bitset存储shape和decoration的对应关系。
#include <iostream>
#include <bitset>
using namespace std;
//***********************常量定义*****************************
const int MAX_NUM = 38;
//*********************自定义数据结构*************************
//********************题目描述中的变量************************
int caseNum;
int pairNum;
//**********************算法中的变量**************************
//存储从shape到decration的映射关系
bitset<MAX_NUM> graph[MAX_NUM];
//***********************算法实现*****************************
//totalNum指当前枚举的K值
//curId指当前检测的shape编号,从1到36依次检测每个shape
//curNum指当前已有的shape数
//maskz值当前的掩码
bool DFS( int totalNum, int curId, int curNum, bitset<MAX_NUM> mask )
{
//必须先检测上次选中的shape是否可行
if( mask.count() < totalNum ) return false;
//如果可行,且数目已足够
if( curNum == totalNum ) return true;
//剪枝
//当加上剩余所有的shape都不够totalNum时, 直接返回,不再搜索
if( curNum + 36 - curId < totalNum ) return false;
//对当前编号的shape有两种选择
//curNum: 不选当前shape,curId+1: 检测下一个
//curNum+1: 选当前shape,mask&graph[curId]: 修改mask
return ( DFS( totalNum, curId+1, curNum, mask ) ||
DFS( totalNum, curId+1, curNum+1, mask&graph[curId] ) );
}
void Init()
{
for( int i=0; i<MAX_NUM; i++ )
{
graph[i].reset();
}
}
void Input()
{
cin >> pairNum;
for( int j=0; j<pairNum; j++ )
{
int shape, decr;
//输入shape、decration的编号,编号范围从1...36
//将编号范围转换到0...35
cin >> shape >> decr;
graph[shape-1].set( decr-1 );
}
}
void Solve()
{
bitset<MAX_NUM> mask;
//把mask的所有位都置1
mask.set();
int k;
//从小到大枚举k, 对每个k值用DFS进行搜索
for( k=2; k*k<=pairNum; k++ )
{
if( !DFS( k, 0, 0, mask ) ) break;
}
cout << k-1 << endl;
}
//************************main函数****************************
int main()
{
freopen( "in.txt", "r", stdin );
cin >> caseNum;
while( caseNum-- )
{
Init();
Input();
Solve();
}
return 0;
}