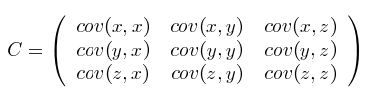PCA中关于协方差矩阵的问题

这段时间因需要用新特征做变换，而不是直接使用原始数据，且原始数据维度太高，故想到PCA降维后再进行操作，这个过程中遇到了一些问题，特此记录，方便自己也方便大家参考。

一、PCA数学理论：

　　关于PCA的理论，资料很多，公式也一大把，本人功底有限，理论方面这里就不列出了。下面主要从应用的角度大概来讲讲具体怎么实现数据集的降维。

1. 把原始数据中每个样本用一个向量表示，然后把所有样本组合起来构成一个矩阵。当然了，为了避免样本的单位的影响，样本集需要标准化。
2. 求该矩阵的协方差矩阵（参考http://www.cnblogs.com/tornadomeet/archive/2012/04/09/2438505.html）。
3. 求步骤2中得到的协方差矩阵的特征值和特征向量。
4. 将求出的特征向量按照特征值的大小进行组合形成一个映射矩阵，并根据指定的PCA保留的特征个数取出映射矩阵的前n行或者前n列作为最终的映射矩阵。
5. 用步骤4的映射矩阵对原始数据进行映射，达到数据降维的目的。

二、遇到的问题

1.关于样本矩阵的组成方式

每个样本都可以看成是一个1*m的行向量，假如有n个样本，则构成的样本矩阵sample维数是n*m，这时，矩阵中每一行代表一个样本，而每一列代表在该维度上n个样本各自的分布情况，因此，在求去除平均值的矩阵meansample时，要对每一列求得平均值，会得到一个1*m的行向量，然后对sample每一行剪掉这个1*m的行向量，这样就可以得到meansample矩阵了。

2.协方差矩阵的构成

大家都知道，利用PCA求特征时，最重要的一步就是要得到样本矩阵的协方差矩阵，从而得到它的特征向量矩阵，根据特征值贡献的不同舍弃部分特征向量后作为投影矩阵，通过对原始数据映射，进而获取了降维后的特征，可用于做分类和识别。如果要查看滤去次要特征后的数据，需要根据降维后的投影矩阵进行反变换，该部分还未研究（http://www.cnblogs.com/tornadomeet/archive/2012/09/06/2673104.html）。

而协方差矩阵的得来是有一些讲究的，协方差是一种用来度量两个随机变量关系的统计量，可表示为：

而对于协方差矩阵，n维的数据集就需要计算个协方差，那自然而然的我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义：

这个定义还是很容易理解的，我们可以举一个简单的三维的例子，假设数据集有三个维度，则协方差矩阵为

可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度上的方差，但是必须要明确一点，协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的，而这也是构成协方差矩阵的基础。对于前面的sample，他的协方差矩阵：

Csample=sample‘*sample，用维数来表示就是m*m=m*nXn*m，

其实想一下就可以理解，对于每个样本，其维度为m，理应用m个特征值来表示它，但这里有一个问题，往往我们在操作的时候m值很大，而协方差矩阵是m*m，对这么大一个矩阵进行求取特征值操作，会是一个相当棘手的问题，我们使用苹果的服务器和iMac（内存6G）进行测试时，发现对降采样后200*200的样本都无法进行计算，会出现内存不足的问题。但是想起来之前有人用这个原始样本380*380进行过pca求解，突然就没搞明白，为什么那个可以做，而现在利用封装好的算法却不行呢，仔细看过才发现，用原始数据运算的算法中没有按照上述定义来求取协方差矩阵，而是使用了另外一个公式：

Vsample=sample*sample’，用维度来表示为n*n=n*mXm*n，

当时感觉这个明显是理解错误，就查阅了下资料，发现已经有同学有过这样的疑问，在iLoveMatlab网站上看到有人说在一个上传代码中有这个问题的解释，因此D了下来，他里面就是用n*n的方法，也说明了根据定义计算会很困难，他替换的理由是对于一个p*r的矩阵，其非零特征值的个数是p-1和r-1中较小的一个，由于在我们处理的问题中p往往要大于r（r为样本个数），因此其特征值个数等价于r-1，这是旧可以用r*pXp*r矩阵的特征值来代替p*rXr*p的特征值，这样做的好处就是大大减小了计算量，但他说的很笼统，借助朋友的提醒，我在KL变换分析中找到了这个做法的合理性解释，它其实是利用了奇异值分解（SVD），下面给出定理内容：

设A是一个秩为r的n*r维矩阵，则存在两个正交矩阵：

以及对角阵

满足

其中：为矩阵和的非零特征值，和分别为和对应于的特征向量。

从上面定理可以看出，和具有相同的特征值，但是特征向量不同，因此利用n*n矩阵来求取m*m矩阵的特征值是可以实现的，这样就是为什么在用n*n矩阵求得的投影矩阵，最后反变换得到的数据和直接用m*m协方差矩阵得到的结果很相似。