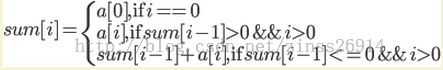首尾相连数组的最大子数组和
前言
这是昨晚参加九度oj的7月份月赛碰到的题目,很有意思,今早查了一下,原来《编程之美》中已经讲过类似题目,看来我把《剑指offer》看完之后,下一本书就是《编程之美》了,今天6点起床想看会英语,可惜还是搞算法了
题目
题目描述: 给定一个由N个整数元素组成的数组arr,数组中有正数也有负数,这个数组不是一般的数组,其首尾是相连的。数组中一个或多个连续元素可以组成一个子数组,其中存在这样的子数组arr[i],…arr[n-1],arr[0],…,arr[j],现在请你这个ACM_Lover用一个最高效的方法帮忙找出所有连续子数组和的最大值(如果数组中的元素全部为负数,则最大和为0,即一个也没有选)。 输入: 输入包含多个测试用例,每个测试用例共有两行,第一行是一个整数n(1=<n<=100000),表示数组的长度,第二行依次输入n个整数(整数绝对值不大于1000)。 输出: 对于每个测试用例,请输出子数组和的最大值。 样例输入: 6 1 -2 3 5 -1 2 5 6 -1 5 4 -7 样例输出: 10 14
这里以 arr[6] = {1, -2, 3, 5, -1, 2}为例做介绍
首尾不相连最大子数组和
这是典型的动态规划题目,假设sum[i]为前i个数据的最大子数组和,则得到状态转移方程为:
有了状态转移方程,代码很容易实现(c语言)
/**
* 首尾不相连
*/
int maxSumNoConnect(int *arr, int n)
{
int i, max, *sum;
sum = (int *)malloc(sizeof(int) * n);
sum[0] = max = arr[0];
for (i = 1; i < n; i ++) {
if (sum[i - 1] > 0)
sum[i] = arr[i] + sum[i - 1];
else
sum[i] = arr[i];
if (sum[i] > max) max = sum[i];
}
free(sum);
return max;
}
可以看到,这里我们用了O(n )的辅助数组sum,可以考虑直接简化辅助空间,代码如下:
int maxSumNoConnectOne(int *arr, int n)
{
int i, max, sum;
max = sum = arr[0] > 0 ? arr[0] : 0;
for (i = 1; i < n; i ++) {
if ((arr[i] + sum) > 0) {
sum += arr[i];
max = max > sum ? max : sum;
} else {
sum = 0;
max = max > arr[i] ? max : arr[i];
}
}
return max;
}
首尾相连最大和子数组
如果数组是首尾相邻的,可以分成两种情况来讨论:
(1) 如果最大和子数组没有跨过首元素,则可以用原问题的解法来求解
(2)如果最大和子数组跨过了首元素,则可以继续分两种情况讨论:
1. 如果数组元素全部为正,则所有元素之和就是最大值
2. 如果数组中有负数,则最大和子数组必然不包括某些元素,而不被包括的元素中必然有最小和子数组,这样我们就可以先查找最小和子数组的最后一个点,并以下一个点为起点,利用(1)的方法循环遍历一遍数组,就可以得到最大和子数组了
图示如下:
(ps:我靠,图片画歪了,算了,大家领会精神就好)
(1)可以用上面首尾不相连的做法求解
(2)的步骤如下
最小和子数组截止坐标
典型的动态规划思想,假设sum[i]为前i个数据的最小子数组和,则得到状态转移方程为:
实现代码(c语言)
/**
* 最小子数组和的截止坐标
*/
int indexInArrMinSum(int *arr, int n)
{
int i, loc, min, *sum;
sum = (int *)malloc(sizeof(int) * n);
min = sum[0] = arr[0];
loc = 0;
for (i = 1; i < n; i ++) {
if (sum[i - 1] > 0) {
sum[i] = arr[i];
} else {
sum[i] = arr[i] + sum[i - 1];
}
if (sum[i] < min) {
loc = i;
min = sum[i];
}
}
free(sum);
return loc;
}
循环遍历
循环遍历只要从最小和子数组截止坐标下一个位置开始即可,无非遍历时需要注意取余而已
/**
* 首尾相连
*/
int maxSumConnect(int *arr, int n)
{
int index, i, loc, cur, max, *sum;
sum = (int *)malloc(sizeof(int) * n);
index = indexInArrMinSum(arr, n);
max = sum[(index + 1) % n] = arr[(index + 1) % n];
for (i = 2; i < n; i ++) { // 不考虑最小子数组的截止坐标了
loc = (index + i - 1) % n;
cur = (index + i) % n;
if (sum[loc] > 0) {
sum[cur] = arr[cur] + sum[loc];
} else {
sum[cur] = arr[cur];
}
if (sum[cur] > max)
max = sum[cur];
}
free(sum);
return max;
}
ac代码
#include <stdio.h>
#include <stdlib.h>
/**
* 首尾不相连
*/
int maxSumNoConnect(int *arr, int n)
{
int i, max, *sum;
sum = (int *)malloc(sizeof(int) * n);
sum[0] = max = arr[0];
for (i = 1; i < n; i ++) {
if (sum[i - 1] > 0)
sum[i] = arr[i] + sum[i - 1];
else
sum[i] = arr[i];
if (sum[i] > max) max = sum[i];
}
free(sum);
return max;
}
/**
* 最小子数组和的截止坐标
*/
int indexInArrMinSum(int *arr, int n)
{
int i, loc, min, *sum;
sum = (int *)malloc(sizeof(int) * n);
min = sum[0] = arr[0];
loc = 0;
for (i = 1; i < n; i ++) {
if (sum[i - 1] > 0) {
sum[i] = arr[i];
} else {
sum[i] = arr[i] + sum[i - 1];
}
if (sum[i] < min) {
loc = i;
min = sum[i];
}
}
free(sum);
return loc;
}
/**
* 首尾相连
*/
int maxSumConnect(int *arr, int n)
{
int index, i, loc, cur, max, *sum;
sum = (int *)malloc(sizeof(int) * n);
index = indexInArrMinSum(arr, n);
max = sum[(index + 1) % n] = arr[(index + 1) % n];
for (i = 2; i < n; i ++) { // 不考虑最小子数组的截止坐标了
loc = (index + i - 1) % n;
cur = (index + i) % n;
if (sum[loc] > 0) {
sum[cur] = arr[cur] + sum[loc];
} else {
sum[cur] = arr[cur];
}
if (sum[cur] > max)
max = sum[cur];
}
free(sum);
return max;
}
int main(void)
{
int i, n, flag, conn_n, conn_y, *arr;
while (scanf("%d", &n) != EOF) {
arr = (int *)malloc(sizeof(int) * n);
for (i = 0, flag = 0; i < n; i ++) {
scanf("%d", arr + i);
if (*(arr + i) <= 0)
flag ++;
}
// 均为负数返回0
if (flag == n) {
printf("0\n");
continue;
}
conn_n = maxSumNoConnect(arr, n);
conn_y = maxSumConnect(arr, n);
if (conn_n < conn_y)
printf("%d\n", conn_y);
else
printf("%d\n", conn_n);
free(arr);
}
return 0;
}
/**************************************************************
Problem: 1527
User: wangzhengyi
Language: C
Result: Accepted
Time:80 ms
Memory:2084 kb
****************************************************************/