Deep learn toolbox：CNN BP求导解析
《Notes on Convolutional Neural Networks》中详细讲解了CNN的BP过程，下面结合Deep learn toolbox中CNN的BP源码对此做一些解析
卷积层：
卷积层的前向传导：
误差反传：
当卷基层的下一层是pooling层时，如果pooling层的误差敏感项为
时，那么卷基层的误差敏感项
为：
其中，upsample表示对进行上采样，
表示激活函数对输入的导数，
代表点积操作
upsample根据pooling时采用方法来定，大概思想为：pooling层的每个节点是由卷积层中多个节点(一般为一个矩形区域)共同计算得到，所以pooling层每个节点的误差敏感值也是由卷积层中多个节点的误差敏感值共同产生的，只需满足两层的误差敏感值总和相等即可，下面以mean-pooling和max-pooling为例来说明。
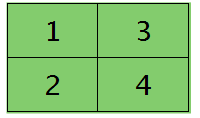
假设卷积层的矩形大小为4×4, pooling区域大小为2×2, 很容易知道pooling后得到的矩形大小也为2*2（本文默认pooling过程是没有重叠的，卷积过程是每次移动一个像素，即是有重叠的，后续不再声明）,如果此时pooling后的矩形误差敏感值如下：
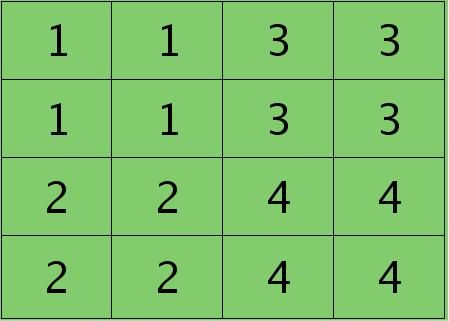
则按照mean-pooling，首先得到的卷积层应该是4×4大小，其值分布为(等值复制)：
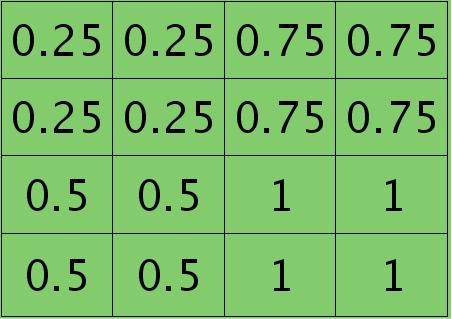
因为得满足反向传播时各层见误差敏感总和不变，所以卷积层对应每个值需要平摊（除以pooling区域大小即可，这里pooling层大小为2×2=4)），最后的卷积层值
分布为：
如果是max-pooling，则需要记录前向传播过程中pooling区域中最大值的位置，这里假设pooling层值1,3,2,4对应的pooling区域位置分别为右下、右上、左上、左下。则此时对应卷积层误差敏感值分布为：
求得后，我们就要求卷积层的导数了，论文中给出的公式为：
上式中
表示的（u，v）项的值，
表示
与
进行卷积的结果
的（u，v）项所对应的的patch。
上述公式和下面的公式是等价的：
损失函数对b的导数为：
deep learn toolbox就是按照上述2个公式计算的。
pooling层的前向传导：
down(.)表示一个下采样函数。典型的操作一般是对输入图像的不同nxn的块的所有像素进行求和。这样输出图像在两个维度上都缩小了n倍。每个输出map都对应一个属于自己的乘性偏置β和一个加性偏置b。
已知卷积层的误差敏感项时，那么pooling层的误差敏感项为：
得到误差敏感项后，由于pooling只有
两个参数，分别求导：
但在deep learn toolbox中，只是简单地进行subsampling,并没有加sigmoid激活函数，因而pooling层没有参数，不需要对pooling层求导，也不
需要对其参数进行更新。
下面是deep learn toolbox 中CNN BP算法的代码：
function net = cnnbp(net, y)
n = numel(net.layers);
// error
net.e = net.o - y;
// loss function
net.L = 1/2* sum(net.e(:) .^ 2) / size(net.e, 2);
//从最后一层的error倒推回来deltas
//和神经网络的bp有些类似
//// backprop deltas
net.od = net.e .* (net.o .* (1 - net.o)); // output delta
net.fvd = (net.ffW' * net.od); // feature vector delta
if strcmp(net.layers{n}.type, 'c') // only conv layers has sigm function
net.fvd = net.fvd .* (net.fv .* (1 - net.fv));
end
//和神经网络类似，参看神经网络的bp
// reshape feature vector deltas into output map style
sa = size(net.layers{n}.a{1});
fvnum = sa(1) * sa(2);
for j = 1 : numel(net.layers{n}.a)
net.layers{n}.d{j} = reshape(net.fvd(((j - 1) * fvnum + 1) : j * fvnum, :), sa(1), sa(2), sa(3));
end
//这是算delta的步骤
//这部分的计算参看Notes on Convolutional Neural Networks，其中的变化有些复杂
//和这篇文章里稍微有些不一样的是这个toolbox在subsampling(也就是pooling层)没有加sigmoid激活函数
//所以这地方还需仔细辨别
//这这个toolbox里的subsampling是不用计算gradient的，而在上面那篇note里是计算了的
for l = (n - 1) : -1 : 1
if strcmp(net.layers{l}.type, 'c')
for j = 1 : numel(net.layers{l}.a)
net.layers{l}.d{j} = net.layers{l}.a{j} .* (1 - net.layers{l}.a{j}) .* (expand(net.layers{l + 1}.d{j}, [net.layers{l + 1}.scale net.layers{l + 1}.scale 1]) / net.layers{l + 1}.scale ^ 2);
end
elseif strcmp(net.layers{l}.type, 's')
for i = 1 : numel(net.layers{l}.a)
z = zeros(size(net.layers{l}.a{1}));
for j = 1 : numel(net.layers{l + 1}.a)
z = z + convn(net.layers{l + 1}.d{j}, rot180(net.layers{l + 1}.k{i}{j}), 'full');
end
net.layers{l}.d{i} = z;
end
end
end
//参见paper，注意这里只计算了'c'层的gradient，因为只有这层有参数
//// calc gradients
for l = 2 : n
if strcmp(net.layers{l}.type, 'c')
for j = 1 : numel(net.layers{l}.a)
for i = 1 : numel(net.layers{l - 1}.a)
net.layers{l}.dk{i}{j} = convn(flipall(net.layers{l - 1}.a{i}), net.layers{l}.d{j}, 'valid') / size(net.layers{l}.d{j}, 3);
end
net.layers{l}.db{j} = sum(net.layers{l}.d{j}(:)) / size(net.layers{l}.d{j}, 3);
end
end
end
//最后一层perceptron的gradient的计算
net.dffW = net.od * (net.fv)' / size(net.od, 2);
net.dffb = mean(net.od, 2);
function X = rot180(X)
X = flipdim(flipdim(X, 1), 2);
end
end