sicily 1206. Stacking Cylinders
解题思路:
(学习了别人的方法,原文地址http://hi.baidu.com/watermoon_littlegui/blog/item/ce42cfecd2c20edcb21cb1d6.html):
同一层每相邻两个可求出上一层的其中一个
直到只剩下一个即是最顶层的那个
知道两点坐标和三边长度(其中两边相等),求第三点的坐标。
已知A、B点坐标以及AC=BC=2,求C点的坐标。
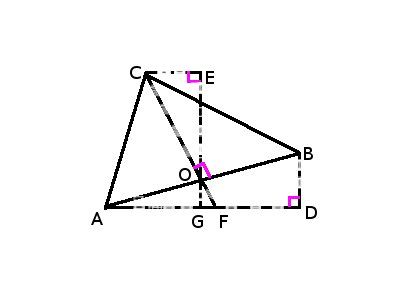
作辅助线AD垂直BD,三角形ABC边AB上的中线AO并延长交AD于F,过0作GE垂直AD于G,
过C做CE垂直G0延长线与E。
AC=BC,O是中点,所有CO垂直AB;
因此C点坐标等于0点坐标加上(或减去OE和CE的长度),O点坐标为(A+B)/2
AB长度由A、B坐标可求,则CO长度len为sqrt( 2^2-(AB/2)^2)
所以只要求得<COE即可求得OE和CE的长度。
由于图中的垂直关系,可以推导出<BAD = <GOF = <COE
sin<BAD = BD / AB = sin<COE
至此,问题就基本解决了,代码如下:
#include <iostream> #include <cstdio> #include <cmath> #include <algorithm> using namespace std; struct Node { double x; double y; } point[20]; int cmp(Node a,Node b) { return a.x < b.x; } int main() { int test,n,i,Case = 1; double dis_x,dis_y,dis; double s,c,len,add_x,add_y; scanf("%d",&test); while(test--) { scanf("%d",&n); for(i = 0;i < n;i++) cin>>point[i].x,point[i].y = 1; sort(point,point+n,cmp); while(n > 1) { for(i = 1;i < n;i++) { dis_x = point[i].x - point[i-1].x; dis_y = point[i].y - point[i-1].y; dis = sqrt(dis_x*dis_x+dis_y*dis_y); //AB的长度 s = (point[i].y-point[i-1].y) / dis;c = (point[i].x-point[i-1].x) / dis;//s代表sine<COE,c代表cosine<COE len = sqrt((2*2) - (dis/2)*(dis/2)); //CO的长度 add_x = len*s;add_y = len*c; //o点相对于C点的x偏移,y偏移 point[i-1].x = (point[i].x+point[i-1].x)/2 - add_x; point[i-1].y = (point[i].y+point[i-1].y)/2 + add_y; } n--; } printf("%d: %.4lf %.4lf/n",Case,point[0].x,point[0].y); Case++; } return 0; }