0001算法笔记——NP完全理论
说来遗憾,在CSDN这么久,一直都是转载和收藏同行精英门写的好文章。这也许就是自己编程水平久久上不去的原因吧,是该改改东一榔头西一棒子的坏习惯了。耶稣说的对,“好记性不如烂笔头”,哥从现在开始要写原创文章了。这篇文章作为算法学习笔记开篇,本人学习算法是看的王晓东的《计算机算法设计与分析》。一开始是买了本《算法导论》,书到的时候翻了翻,砖头啊,那个难度恐怕乔帮主在世也未必能琢磨得透吧。还是看国产的书容易些,文字叙述方式、难度、内容适合现阶段水平。
第一章,算法概述,定义什么的,复杂度什么的没有什么新鲜的,是个程序员都知道。相对来时,值得一提的是NP完全性理论。累赘的话不多说,直接来几个定义:
多项式时间:在计算复杂度理论中,指的是一个问题的计算时间m(n)不大于问题大小n的多项式倍数。通俗点来说,多项式时间就是指时间复杂度是个多项式,或者说,就是这个程序运行的时间随着数据规模n变化的函数为f(n),那么,f(n)是个多项式函数,那么就可以说是控制在多项式之内。举个例子,现在从n阶图中找两点的最短路径,复杂度为n^2级别(即O(n^2),O是大写欧),而n^2对于n是多项式(单项式当然也算),这就称为是多项式复杂度,或者多项式时间,其中问题(算法)的规模是n。如果某一个算法的规模是n,但是复杂度比如是2^n,写不成n的多项式,那就不是多项式时间。
P类问题:所有可以在多项式时间内求解的判定问题构成P类问题。判定问题:判断是否有一种能够解决某一类问题的能行算法的研究课题。
NP类问题:所有的非确定性多项式时间可解的判定问题构成NP类问题。非确定性算法:非确定性算法将问题分解成猜测和验证两个阶段。算法的猜测阶段是非确定性的,算法的验证阶段是确定性的,它验证猜测阶段给出解的正确性。设算法A是解一个判定问题Q的非确定性算法,如果A的验证阶段能在多项式时间内完成,则称A是一个多项式时间非确定性算法。有些计算问题是确定性的,比如加减乘除之类,你只要按照公式推导,按部就班一步步来,就可以得到结果。但是,有些问题是无法按部就班直接地计算出来。比如,找大质数的问题。有没有一个公式,你一套公式,就可以一步步推算出来,下一个质数应该是多少呢?这样的公式是没有的。再比如,大的合数分解质因数的问题,有没有一个公式,把合数代进去,就直接可以算出,它的因子各自是多少?也没有这样的公式。这种问题的答案,是无法直接计算得到的,只能通过间接的“猜算”来得到结果。这也就是非确定性问题。而这些问题的通常有个算法,它不能直接告诉你答案是什么,但可以告诉你,某个可能的结果是正确的答案还是错误的。这个可以告诉你“猜算”的答案正确与否的算法,假如可以在多项式(polynomial)时间内算出来,就叫做多项式非确定性问题。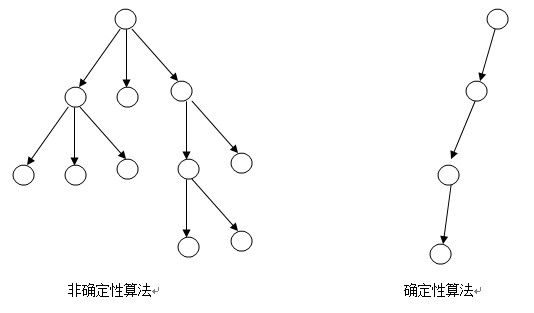
NPC问题:NP中的某些问题的复杂性与整个类的复杂性相关联.这些问题中任何一个如果存在多项式时间的算法,那么所有NP问题都是多项式时间可解的.这些问题被称为NP-完全问题(NPC问题)。
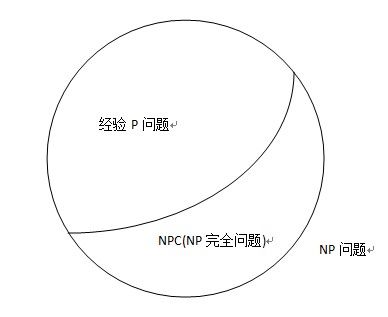
P类问题,NP类问题,NPC之间的关系可有下图(此图正确性有待证明)表示:
总结:P类问题是可以在多项式时间内解决的,polynomial problem。
NP类问题,可以在多项式的时间里验证一个解的问题,non deterministic polynomial
NPC问题,最不可能转换为p决定的问题的集合,np complete