log1p(x) 和 expm1(x) 函数的实现
double log1p (const double x); double expm1(double x);
这两个C语言的函数在C89标准中是没有的。但是在大多数的UNIX或类UNIX 系统平台上的C语言数学函数库都提供了这两个函数。C99 标准中应该也将这两个函数包含了进去(我手头上没有C99 标准文档,所以是不是都包含进去了不是十分肯定)。
这两个函数的功能如下:
log1p(x) := log(1+x)
expm1(x) := exp(x) - 1
初一看这两个函数,给人的第一印象似乎这两个函数都是多余的。用上这两个函数还降低了程序的可读性,毕竟这两个函数不是那种一看到名字立刻能明白含义的。
但是仔细分析后就会发现这两个函数的作用是不能替代的,至少都不是能很容易的实现的。
数值分析(计算数学)课上讲过两种最常见的浮点数运算过程中损失有效数字的情况。
- 两个相近的数相减
- 两个数量级相差很大的数字相加减
这两种情况正好就在这两个函数的实现中会碰到。
log1p(x)
先来说log1p(x),当x很小时,比如 x=10-16,1+x = 1。因为 double 型只有不超过16位的有效数字。
如果用 log(x+1) 来计算,得到的结果为 0。而利用maxima用50位10进制精度来计算得到的结果是9.9999999999999994450522627913249426863455887780845e-17。
如果考虑到double 型变量只有约16位的有效数字,那么准确的结果应该为: 1.000000000000000e-16。可见,这个极端的情况下,直接利用log(x+1)来计算,得到的结果的有效数字为0位。即使x大一些,比如 x=10-12 ,16位有效数字的结果为9.999999999995000e-13。这时用 log(x+1) 来计算的结果为1.000088900581841e-12。有效数字也只有前5位,后面的数字完全不正确。
准确的计算log1p(x)的值,尤其是当x很小时是一个蛮有挑战的事情。如果我们再要求计算结果可以保证有15位以上的有效数字时这个问题就更难了。
下面先给出一种最简单的实现方式,是我在一个网站上找到的:
http://www.johndcook.com/cpp_log_one_plus_x.html
double log1p(const double x)
{
if (fabs(x) > 1e-4)
{
// x is large enough that the obvious evaluation is OK
return log(1.0 + x);
}
// Use Taylor approx. log(1 + x) = x - x^2/2 with error roughly x^3/3
// Since |x| < 10^-4, |x|^3 < 10^-12, relative error less than 10^-8
return (-0.5 * x + 1.0) * x;
}
这个代码的想法很简单,当 x 较大时直接计算。x 很小时用泰勒展开来计算。我们知道:
如果我们取前两项作为近似结果,那么截断误差大约为 x^3 ,据此可以估算有效数字,当然也可以直接计算,我们知道误差最大的点肯定是x=1e-4 时。简单计算一下可知,当x=1e-4 时,用 log(1.0 + x) 计算的 有效数字有12位,用 (-0.5 * x + 1.0) * x 计算的结果的有效数字有 8 位。说明这种方法的有效数字至少可以保证有 8位。对于大多数的计算已经够用了。不过我们的目标是15位有效数字,因此还要再努努力。
上面的方法中泰勒展开只用到了前两项,如果我们多用几项肯定效果会更好。下面我们取前三项。
double log1p(const double x)
{
if (fabs(x) > 1e-4)
{
// x is large enough that the obvious evaluation is OK
return log(1.0 + x);
}
return(x * (x * (2 * x - 3) + 6)) / 6;
}
这时有效数字提升到了12位,我们又前进了一步。
下面给个 GSL 库中的实现。
double gsl_log1p (const double x)
{
volatile double y, z;
y = 1 + x;
z = y - 1;
return log(y) - (z - x) / y ; /* cancels errors with IEEE arithmetic */
}
经过实际验算,这个算法可以保证15位的有效数字。很神奇的算法,先计算 log (1+x),然后在做修正,而且只做了个1阶修正就能达到如此好效果,很让我惊讶。为什么会这样我现在的水平还解释不了。
大名鼎鼎的统计软件 R 的代码中也包含了一个他们自己实现的 log1p(x) 函数,实现的方式是另一套思路,用的是切比雪夫逼近。基本上是将 Los Alamos Scientific Laboratory 的 W. Fullerton 用 Fortran 语言写的dlnrel 翻译成了 C 代码。
代码在:http://svn.r-project.org/R/trunk/src/nmath/log1p.c
expm1(x)
expm1(x) = exp(x) - 1
当x很小的时候,exp(x) 很接近 1。两个很接近的数字相减同样会导致有效数字急剧减少。比如当 x = 1e-15 时。Exp(x)-1 = 1.00000000000e-15
而如果用 double 型浮点数来计算,得到的结果是1.1102230246251565e-15。有效数字只有1位,后面的数字都是错误的。
解决的方法很多,我们还可以使用泰勒展开来处理。
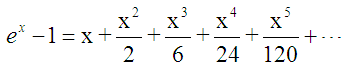
可以看到这个级数收敛的很快,因此我们只要取很少的几项就能得到很高的计算精度。
下面的代码来自:http://www.johndcook.com/cpp_expm1.html
double expm1(double x)
{
if(fabs(x) < 1e-5)
return x + 0.5 * x * x;
else
return exp(x) - 1.0;
}
计算可知,这个代码可以保证至少有10位有效数字。
下面给出 GSL 库中的代码,这个代码可以保证 15 位有效数字。
#define GSL_DBL_EPSILON 2.2204460492503131e-16
#define M_LN2 0.69314718055994530941723212146 /* ln(2) */
double gsl_expm1 (const double x)
{
/* FIXME: this should be improved */
if (fabs(x) < M_LN2)
{
/* Compute the taylor series S = x + (1/2!) x^2 + (1/3!) x^3 + ... */
double i = 1.0;
double sum = x;
double term = x / 1.0;
do
{
i++ ;
term *= x/i;
sum += term;
}
while (fabs(term) > fabs(sum) * GSL_DBL_EPSILON) ;
return sum ;
}
else
{
return exp(x) - 1;
}
}
这个代码的缺点在于(1)循环的次数不定,对于实时系统来说不太方便(2)效率上还有提高的余地。
相比来说,统计软件 R 中的代码就更好一些。先用泰勒展开式做为初值,然后用牛顿迭代法做修正。牛顿迭代法是二阶收敛的,我们的初值的误差本来就很小,因此迭代一次就足以满足我们对有效数字的要求了。
http://svn.r-project.org/R/trunk/src/nmath/expm1.c
double expm1(double x)
{
double y, a = fabs(x);
if (a < DBL_EPSILON) return x;
if (a > 0.697) return exp(x) - 1; /* negligible cancellation */
if (a > 1e-8)
y = exp(x) - 1;
else /* Taylor expansion, more accurate in this range */
y = (x / 2 + 1) * x;
/* Newton step for solving log(1 + y) = x for y : */
/* WARNING: does not work for y ~ -1: bug in 1.5.0 */
y -= (1 + y) * (log1p (y) - x);
return y;
}
不过上面的代码中也指出了,当 y 接近 -1 时,也就是 x 为负的很大的数时,上面的方法失效。
很遗憾,直到现在我还没能找到一个让我非常满意的expm1() 函数的实现方式。
