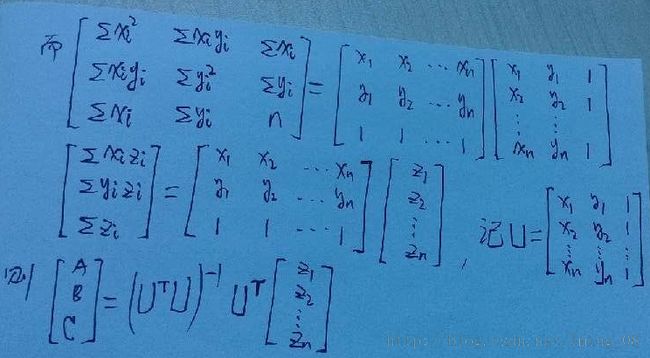基于最小二乘法估计点云的曲面法向量
之前对PCL库计算三维点云数据的曲面法向量有过介绍， 点云的曲面法向量估计，PCL库是采用主成份分析方法的，近几天通过理论推导发现最小二乘法应该也能计算曲面法向量。首先介绍下其理论知识。
估计某个点的法向量，可以类似于 点云的曲面法向量估计，将该点附近K近邻的点近似在一个局部平面上，之后就通过最小二乘法拟合该平面方程，通过高等数学空间解析几何知识可知，若平面方程为A*x + B*y + C*z + D = 0，则平面法向量就是(A, B, C)；从而求出法向量。
本文的最小二乘法估计法向量，主要在computePointNormal()实现：
编写完以上代码后，编译PCL源码，生成新的pcl_features_debug.lib和pcl_features_debug.dll库；然后编写测试程序，并引用pcl_features_debug.lib和pcl_features_debug.dll库。
这里构造一个平面方程为x + y + z = 1的平面：
尽管上述结果不错，但是如果修改下平面点云的构造，
估计某个点的法向量，可以类似于 点云的曲面法向量估计，将该点附近K近邻的点近似在一个局部平面上，之后就通过最小二乘法拟合该平面方程，通过高等数学空间解析几何知识可知，若平面方程为A*x + B*y + C*z + D = 0，则平面法向量就是(A, B, C)；从而求出法向量。
这里将平面方程转化为z = A*x + B*y + C，最小二乘法推导过程如下：
汗！图片手机照的，没带数据线，通过QQ传到网上后，图片质量降低！回去再替换。
根据以上推导出的最终结果，基于PCL库和Eigen库编程实现法向量估计：
原PCL库中法向量估计相关类为NormalEstimation，这里往PCL源码pcl_features工程下添加normal_esti_leastsquare.h、normal_esti_leastsquare.hpp、normal_esti_leastsquare.cpp文件，相关类名NormalEstimation2。
主要代码如下所示：
for (size_t idx = 0; idx < indices_->size (); ++idx)
{
if (this->searchForNeighbors ((*indices_)[idx], search_parameter_, nn_indices, nn_dists) == 0)
{
output.points[idx].normal[0] = output.points[idx].normal[1] = output.points[idx].normal[2] = output.points[idx].curvature = std::numeric_limits<float>::quiet_NaN ();
output.is_dense = false;
continue;
}
computePointNormal (*surface_, nn_indices,
output.points[idx].normal[0], output.points[idx].normal[1], output.points[idx].normal[2], output.points[idx].curvature);
//flipNormalTowardsViewpoint (input_->points[(*indices_)[idx]], vpx_, vpy_, vpz_,
// output.points[idx].normal[0], output.points[idx].normal[1], output.points[idx].normal[2]);
}上述代码与NormalEstimation类的对应代码相差无几，都是采用K近邻法获取每个点附近的点，然后基于这些点计算该点的法向量。
本文的最小二乘法估计法向量，主要在computePointNormal()实现：
/** \brief 计算点的法向量，曲率暂时不求
* \param[in] 输入点云
* \param[in] 给定点的索引下标
* \param[out] 法向量x分量
* \param[out] 法向量y分量
* \param[out] 法向量z分量
* \param[out] 曲率
*/
inline void
computePointNormal (const pcl::PointCloud<PointInT> &cloud, const std::vector<int> &indices, float &nx, float &ny, float &nz, float &curvature)
{
u_matrix_.resize(k_ , 3);
Eigen::VectorXf z_vec(k_);
for (size_t i = 0, ind_num = indices.size(); i < ind_num; ++i)
{
size_t indice = indices[i];
u_matrix_(i, 0) = cloud.points[indice].x;
u_matrix_(i, 1) = cloud.points[indice].y;
u_matrix_(i, 2) = 1;
z_vec[i] = cloud.points[indice].z;
}
EIGEN_ALIGN16 Eigen::Matrix3f utu_matrix = u_matrix_.transpose() * u_matrix_;
EIGEN_ALIGN16 Eigen::Vector3f solve_vec = utu_matrix.inverse() * u_matrix_.transpose() * z_vec;
EIGEN_ALIGN16 Eigen::Vector3f normal_vec(solve_vec[0], solve_vec[1], -1);
normal_vec /= normal_vec.squaredNorm(); //归一化为单位向量
nx = normal_vec[0];
ny = normal_vec[1];
nz = normal_vec[2];
}
编写完以上代码后，编译PCL源码，生成新的pcl_features_debug.lib和pcl_features_debug.dll库；然后编写测试程序，并引用pcl_features_debug.lib和pcl_features_debug.dll库。
这里构造一个平面方程为x + y + z = 1的平面：
#include <iostream>
#include <pcl/point_types.h>
#include <pcl/io/pcd_io.h>
#include <pcl/features/normal_esti_leastsquare.h>
using namespace std;
int main(int argc, char* argv[])
{
pcl::PointCloud<pcl::PointXYZ>::Ptr inCloud(new pcl::PointCloud<pcl::PointXYZ>);
pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>);
for (float x = -5.0; x <= 5.0; x += 0.25)
{
for (float y = -5.0; y <= 5.0; y += 0.25)
{
pcl::PointXYZ cloud;
cloud.x = x;
cloud.y = y;
cloud.z = 1 - x - y;
inCloud->push_back(cloud);
}
}
tree.reset (new pcl::search::KdTree<pcl::PointXYZ> (false));
tree->setInputCloud (inCloud);
// Normal estimation
pcl::NormalEstimation2<pcl::PointXYZ, pcl::Normal> ne2;
pcl::PointCloud<pcl::Normal>::Ptr normals (new pcl::PointCloud<pcl::Normal> ());
ne2.setInputCloud (inCloud);
ne2.setSearchMethod (tree);
ne2.setKSearch (20);
ne2.compute (*normals);
pcl::PointCloud<pcl::PointNormal>::Ptr cloud_with_normals(new pcl::PointCloud<pcl::PointNormal>);
pcl::concatenateFields(*inCloud, *normals, *cloud_with_normals);
pcl::io::savePCDFile("plane_cloud_out.pcd", *cloud_with_normals);
}查看生成的plane_cloud_out.pcd文件内容，
# .PCD v0.7 - Point Cloud Data file format VERSION 0.7 FIELDS x y z intensity normal_x normal_y normal_z curvature SIZE 4 4 4 4 4 4 4 4 TYPE F F F F F F F F COUNT 1 1 1 1 1 1 1 1 WIDTH 1681 HEIGHT 1 VIEWPOINT 0 0 0 1 0 0 0 POINTS 1681 DATA ascii -5 -5 11 0 -0.33333454 -0.3333388 -0.33334672 -1.0737418e+008 -5 -4.75 10.75 0 -0.33333459 -0.33333915 -0.33334744 -1.0737418e+008 -5 -4.5 10.5 0 -0.33333349 -0.33333221 -0.33333147 -1.0737418e+008 -5 -4.25 10.25 0 -0.33333686 -0.33333236 -0.33333844 -1.0737418e+008 -5 -4 10 0 -0.33332857 -0.33334196 -0.33334109 -1.0737418e+008 -5 -3.75 9.75 0 -0.33333248 -0.33333272 -0.33333042 -1.0737418e+008 -5 -3.5 9.5 0 -0.33333799 -0.33333102 -0.33333802 -1.0737418e+008 -5 -3.25 9.25 0 -0.33333382 -0.33333775 -0.33334321 -1.0737418e+008 -5 -3 9 0 -0.33334044 -0.33332446 -0.3333298 -1.0737418e+008 -5 -2.75 8.75 0 -0.33333328 -0.33333099 -0.3333286 -1.0737418e+008 -5 -2.5 8.5 0 -0.33333698 -0.33332804 -0.33333004 -1.0737418e+008 -5 -2.25 8.25 0 -0.33332828 -0.33334482 -0.33334616 -1.0737418e+008 -5 -2 8 0 -0.33332947 -0.33334234 -0.33334357 -1.0737418e+008 -5 -1.75 7.75 0 -0.33333299 -0.3333362 -0.33333835 -1.0737418e+008 -5 -1.5 7.5 0 -0.33333793 -0.33332565 -0.33332711 -1.0737418e+008 -5 -1.25 7.25 0 -0.33333275 -0.33333525 -0.333336 -1.0737418e+008 -5 -1 7 0 -0.33333316 -0.33333406 -0.33333445 -1.0737418e+008 -5 -0.75 6.75 0 -0.33333361 -0.33333287 -0.3333329 -1.0737418e+008 -5 -0.5 6.5 0 -0.33333489 -0.33332995 -0.33332968 -1.0737418e+008 ... ... ...可以看出各点的法向量近似与(1, 1, 1)共线，这与从平面方程x + y + z = 1中得出的平面法向量保持一致！可以看出计算效果非常理想。
尽管上述结果不错，但是如果修改下平面点云的构造，
//减小步长，由0.25减到0.1
for (float x = -5.0; x <= 5.0; x += 0.1)
{
for (float y = -5.0; y <= 5.0; y += 0.1)
{
pcl::PointXYZ cloud;
cloud.x = x;
cloud.y = y;
cloud.z = 1 - x - y;
inCloud->push_back(cloud);
}
} 再次执行测试程序，生成plane_cloud_out.pcd文件内容，
# .PCD v0.7 - Point Cloud Data file format VERSION 0.7 FIELDS x y z intensity normal_x normal_y normal_z curvature SIZE 4 4 4 4 4 4 4 4 TYPE F F F F F F F F COUNT 1 1 1 1 1 1 1 1 WIDTH 10201 HEIGHT 1 VIEWPOINT 0 0 0 1 0 0 0 POINTS 10201 DATA ascii -5 -5 11 0 -0.36251435 -0.33222172 -0.40937933 -1.0737418e+008 -5 -4.9000001 10.9 0 -0.2965593 -0.36960894 -0.34049508 -1.0737418e+008 -5 -4.8000002 10.8 0 -0.30257833 -0.32366723 -0.26829782 -1.0737418e+008 -5 -4.7000003 10.700001 0 -0.32577419 -0.35322508 -0.36178556 -1.0737418e+008 -5 -4.6000004 10.6 0 -0.34574831 -0.31297931 -0.31971669 -1.0737418e+008 -5 -4.5000005 10.5 0 -0.3243891 -0.34880957 -0.34800133 -1.0737418e+008 -5 -4.4000006 10.400001 0 -0.31732634 -0.34978729 -0.33582667 -1.0737418e+008 -5 -4.3000007 10.300001 0 -0.32080838 -0.33909816 -0.32085085 -1.0737418e+008 -5 -4.2000008 10.200001 0 -0.3384032 -0.33768722 -0.35353974 -1.0737418e+008 -5 -4.1000009 10.1 0 -0.34146273 -0.31813207 -0.32056987 -1.0737418e+008 -5 -4.000001 10.000001 0 -0.3408044 -0.32376921 -0.32963032 -1.0737418e+008 -5 -3.900001 9.9000015 0 -0.29470387 -0.359045 -0.31496942 -1.0737418e+008 -5 -3.8000011 9.8000011 0 -0.35997671 -0.31077951 -0.34562108 -1.0737418e+008 -5 -3.7000012 9.7000008 0 -0.32181746 -0.33056432 -0.30722877 -1.0737418e+008 -5 -3.6000013 9.6000013 0 -0.32655463 -0.3454251 -0.34494016 -1.0737418e+008 -5 -3.5000014 9.5000019 0 -0.35073376 -0.32577616 -0.35558489 -1.0737418e+008 -5 -3.4000015 9.4000015 0 -0.34808326 -0.32221347 -0.3418338 -1.0737418e+008 -5 -3.3000016 9.3000011 0 -0.3261568 -0.33644432 -0.32556668 -1.0737418e+008 ... ... ...可以看出每个点的法向量不再近似共线于(1, 1, 1)。原因暂时还不清楚，个人推测为最小二乘法拟合平面适用于稀疏点集，密集点云并不适合， 原因可能是密集点时u_matrix_
各行向量非常近似于平行，导致行列式为0，无法求得正确的逆矩阵，而以上计算过程中是用到了逆矩阵；
【2014-03-16】今天偶然看到一篇文章介绍最小二乘法的缺陷，http://www.cnblogs.com/jerrylead/archive/2011/08/21/2148625.html
如果样例数m相比特征数n少（m<n）或者特征间线性相关时，由于
（n*n矩阵）的秩小于特征个数（即![clip_image002[1]](http://img.e-com-net.com/image/info5/4b405a89df1244e6b2d725267912f13b.png "clip_image002[1]"){kind=small}
不可逆）。因此最小二乘法
就会失效。
可以看出来，样本矩阵的x、y、z三个列向量近乎于共线，当然也近乎于线性相关，如果真是这样，那么这里最小二乘法并不适用！
真实原因有哪位朋友知道的话望告知！
虽然点云密集时，计算出的法向量不够准，但经过实践发现，增加点K近邻的样本个数(即增加K邻近算法中的K值，本例中为k_)，计算出的法向量是可以近似共线于(1,1,1)。
个人分析，这里增加点近邻的样本个数，实际上也是减小样本矩阵的x、y、z三个列向量的共线程度，所以增加点近邻的样本个数后，就可以使用最小二乘法了。
对于稀疏点云，以上拟合方式大多数情况下是可以的，但若平面与Z轴平行，则不可行，因为此时平面方程是无法转化为z = A*x + B*y + C形式。下面针对平面方程最原始的一般式进行推导，过程如下：
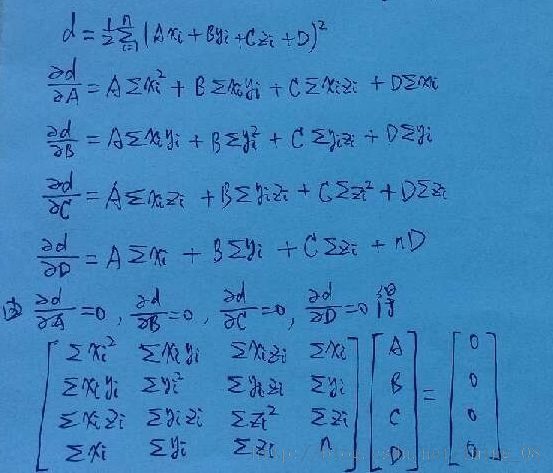
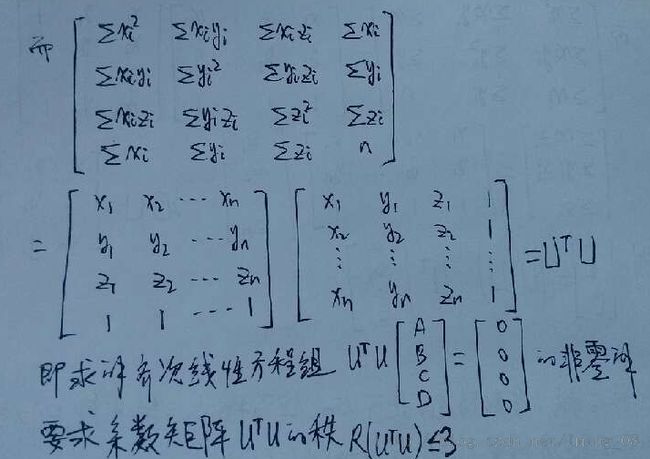
注意，这里U^T*U是一个4*4的方阵，求齐次线性方程组的非零解，问题可以转换为求一个系数为3*3的方阵对应的齐次线性方程组，
类似地，可以将以上结论延伸至系数矩阵为4*4方阵对应的齐次线性方程组：
由此得到齐次线性方程组的非零解。
采用该方法，编程实现：
/** \brief 计算点的法向量，曲率暂时不求
* \param[in] 输入点云
* \param[in] 给定点的索引下标
* \param[out] 法向量x分量
* \param[out] 法向量y分量
* \param[out] 法向量z分量
* \param[out] 曲率
*/
inline void
computePointNormal (const pcl::PointCloud<PointInT> &cloud, const std::vector<int> &indices, float &nx, float &ny, float &nz, float &curvature)
{
Eigen::MatrixX4f mat_ext(k_, 4);
for (size_t i = 0, ind_num = indices.size(); i < ind_num; ++i)
{
size_t indice = indices[i];
mat_ext(i, 0) = cloud.points[indice].x;
mat_ext(i, 1) = cloud.points[indice].y;
mat_ext(i, 2) = cloud.points[indice].z;
mat_ext(i, 3) = 1;
}
Eigen::MatrixXf mat_mult_ext = mat_ext.transpose() * mat_ext; //mat是3*k_矩阵，mat_ext是k_*4矩阵
// A*x = b, A.Row(0).cross(A.Row(1)) = eigenvector(0);
Eigen::Vector4f row_vec[3];
row_vec[0] = mat_mult_ext.row(0);
row_vec[1] = mat_mult_ext.row(1);
row_vec[2] = mat_mult_ext.row(2);
Eigen::Matrix3f i_cofactor, j_cofactor, k_cofactor, l_cofactor; //计算叉积时，i、j、k、l分量的代数余子式
for (size_t row_index = 0; row_index < 3; ++row_index)
{
for (size_t col_index = 0; col_index < 3; ++col_index)
{
i_cofactor(row_index , col_index) = row_vec[row_index][col_index + 1];
if (col_index < 1)
{
j_cofactor(row_index , col_index) = row_vec[row_index][col_index];
}
else
{
j_cofactor(row_index , col_index) = row_vec[row_index][col_index + 1];
}
if (col_index < 2)
{
k_cofactor(row_index , col_index) = row_vec[row_index][col_index];
}
else
{
k_cofactor(row_index , col_index) = row_vec[row_index][col_index + 1];
}
l_cofactor(row_index , col_index) = row_vec[row_index][col_index];
}
}
float i_dim = 0, j_dim = 0, k_dim = 0, l_dim = 0;
i_dim = i_cofactor.determinant();
j_dim = j_cofactor.determinant();
k_dim = k_cofactor.determinant();
l_dim = l_cofactor.determinant();
Eigen::Vector3f coeff_vec(i_dim, -j_dim, k_dim);
float len = coeff_vec.squaredNorm();
coeff_vec /= len;
nx = coeff_vec[0];
ny = coeff_vec[1];
nz = coeff_vec[2];
}采用以上方法实现后，编译PCL源码得到对应的库文件，然后测试程序引用，执行后生成的plane_cloud_out.pcd文件内容为：
# .PCD v0.7 - Point Cloud Data file format VERSION 0.7 FIELDS x y z intensity normal_x normal_y normal_z curvature SIZE 4 4 4 4 4 4 4 4 TYPE F F F F F F F F COUNT 1 1 1 1 1 1 1 1 WIDTH 1681 HEIGHT 1 VIEWPOINT 0 0 0 1 0 0 0 POINTS 1681 DATA ascii -5 -5 11 0 0.0034180761 0.003418348 0.0033811682 -1.0737418e+008 -5 -4.75 10.75 0 0.0034180761 0.003418348 0.0033811682 -1.0737418e+008 -5 -4.5 10.5 0 0.0036986405 0.0036108212 0.0036840038 -1.0737418e+008 -5 -4.25 10.25 0 0.0041074576 0.0039950516 0.0042172931 -1.0737418e+008 -5 -4 10 0 0.0040342622 0.004034651 0.0041443072 -1.0737418e+008 -5 -3.75 9.75 0 0.004033945 0.0041615977 0.0040161251 -1.0737418e+008 -5 -3.5 9.5 0 0.0041075312 0.0040329853 0.0041812863 -1.0737418e+008 -5 -3.25 9.25 0 0.0040594526 0.0040964941 0.0040962985 -1.0737418e+008 -5 -3 9 0 0.0040834057 0.0040837992 0.0041210586 -1.0737418e+008 -5 -2.75 8.75 0 0.0041877129 0.0040933029 0.0041687908 -1.0737418e+008 -5 -2.5 8.5 0 0.0040593483 0.0040955977 0.0040955977 -1.0737418e+008 -5 -2.25 8.25 0 0.0040110592 0.0041013826 0.0040649828 -1.0737418e+008 -5 -2 8 0 0.0040473556 0.0040835626 0.0040469691 -1.0737418e+008 -5 -1.75 7.75 0 0.0040717809 0.0040713926 0.0040715868 -1.0737418e+008 -5 -1.5 7.5 0 0.004047934 0.0040837578 0.0040467749 -1.0737418e+008 -5 -1.25 7.25 0 0.0040838025 0.004065339 0.0040841922 -1.0737418e+008 -5 -1 7 0 0.0040716026 0.0040716026 0.0040712142 -1.0737418e+008 -5 -0.75 6.75 0 0.0040599061 0.0040774848 0.0040595187 -1.0737418e+008 -5 -0.5 6.5 0 0.0040714089 0.0040717972 0.0040717972 -1.0737418e+008 -5 -0.25 6.25 0 0.0040713926 0.0040717809 0.0040715868 -1.0737418e+008 -5 0 6 0 0.0040716026 0.0040712142 0.0040716026 -1.0737418e+008 -5 0.25 5.75 0 0.0040713926 0.0040715868 0.0040717809 -1.0737418e+008 -5 0.5 5.5 0 0.0040714089 0.0040717972 0.0040717972 -1.0737418e+008 ... ... ...
可以看到点云中每个点对应的法向量也都近似共线于(1, 1, 1)。与之前解非其次线性方程组的方法类似，当点云数据比较密集(点与点间距离很小)时，计算出来的结果也是很不准的；同样地，增加点K近邻的样本个数(即增加K邻近算法中的K值，本例中为k_)，计算出的法向量是可以近似共线于(1,1,1)。个人推测的原因见文章之前部分。
还是那句话，真实原因有哪位朋友知道的话望告知！
完整代码可以下载http://download.csdn.net/detail/lming_08/7035195。