启发式路径搜索（1）

                            启发式路径搜索

目录

一  题目背景 1

二  方法提炼 2

三  Demo 2

四  优化启发式搜索 5

一  题目背景

我们玩游戏时，经常点击一下鼠标，游戏角色就会自动按照最短路径走向目的地，这需要搜索最短路径，这都是游戏程序帮我们完成了。游戏程序是如何做到高效完成的呢？

常规的最短路径搜索用深度优先搜索，宽度优先搜索Dijstra算法等，宽度优先算法和Dijstra都是贪心为主的算法，但这几个算法效果并不好，几乎把整个图搜索了一遍，这可能会降低游戏性能。

这些算法都有个特点，没有利用地图自身的特点，假设初始点start， 目的点end，当前点cur，这时我们找到了若干个当前点：

节点       间隔    节点      前后间隔      节点

Start       101     Cur1       1000         End

Start       102     Cur2       500          End

Start       103     Cur3       100          End

按照上面这个例子，起点到Cur1时101距离  而Cur1到终点是预估1000距离

起点到Cur2时102距离  而Cur2到终点是预估500距离

起点到Cur3时103距离  而Cur2到终点是预估100距离

预估距离：因为并没有真实遍历，距离只能通过一些简单的规则预估，比如通过|x|+|y|

按照宽度优先或者Dijstra算法，这里会优先计算第一条路径的可能性，但实际中第三条路径可能性最大，所以如果在选择相对较好的路径时，考虑上预估路径，那么我们就会选择第三个方案，这样一来就会大大减少冗余数据，提高搜索速度。  如图：

  我们优先搜索节点N还是节点M？  

  按照Dijstra会搜索节点M，但我们搜索节点N。 因为节点N距离终点的预估值只有27（加上已知距离是52），二节点M到终点的预估值是60（加上已知距离是75）。

二 方法提炼

F（n） = G（n) + H(n);

F(n) 表示从起点到终点经过n这个节点的可能距离。其中

G（n)是起点到节点N的最短距离（这个是贪心遍历出来的）；

H（n)是节点N到终点的预估距离。

一般的Dijstra算法是没有H（n)的相当于H(n)是0. 这里面考虑到预估距离就是启发式搜索。通过已知节点，找出相邻的节点，计算相邻节点的F(n),然后寻找最优的。

这样我们每次通过一个已知确定路径的节点，可以遍历出8个新节点，这个8个节点，就都有了一个最新的G（n), 同时给他们计算上相应的H(n)。当然G(n)可能被更小的值替换。

证明：启发式搜索一定是最优解么？

证： 当H（n）小于等于真实距离是真实解，因为通过F（n）的比较每次被临时放弃的节点都是因为自己的F（n）比别人的大，而自己的G（n）是真实距离，H（n）又小于等于真实距离，所以这个被放弃的点在这一步的确不是最优解，直到它可能是最优解的时候它才会被搜索。  故得证。 

三 Demo

    

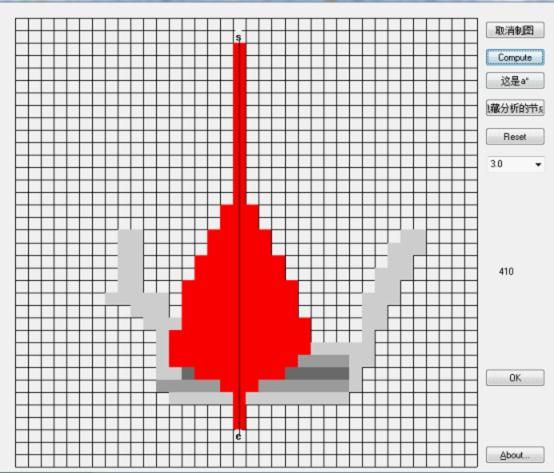
做了一个例子，假设每个节点横跨需要10距离，那么斜传就需要14距离，节点分为5种：距离10、距离20、距离30、距离40以及障碍（障碍不能穿过）。 从节点A走到相邻的节点B，需要距离 （距离A+距离B）/2,  如果是斜走，则是14的倍数那个值。

预估距离：

当前节点 x,y    终点ex  ey.

nMax = 节点N距离终点的长距。

nMin = 节点N距离终点的短距。

H(n) = sqrt(nMin *nMin *2) + （nMax -nMin）.

地图如下：

 

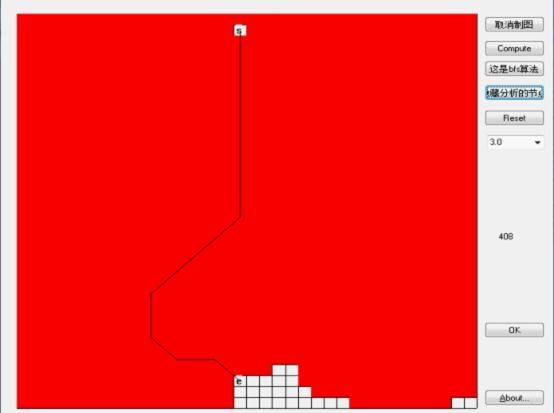
1  原图，以及通过Dijstra算法的最短路线如图，距离是408（这是最优解）。

   

 

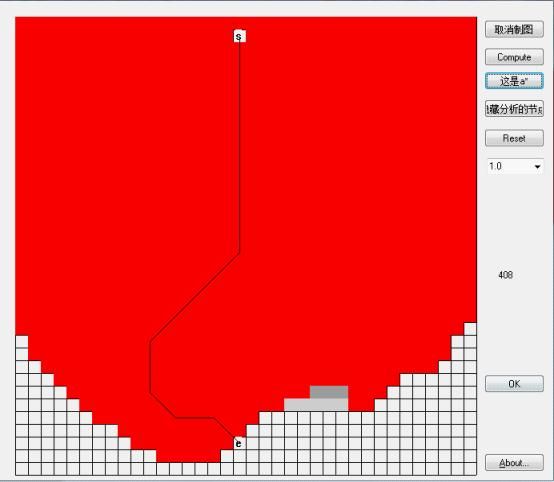
   这是Dijstra算法搜索过的节点，可见他几乎遍历了整个图，效率肯定就不高了。

   这是启发式搜索，可见他搜索的面积比BFS相对小了一些，但效果也不是很好。

四  优化启发式搜索

为什么我们加入了启发式搜索，效果还不是太好呢？ 这个和选择的图片关系很大，因为这个图片在最合适的地方加了一堆障碍，导致启发式搜索不得不搜索更远的节点来对比。但我们还能优化。

优化思路： 我们的预估都是按照理论上的最小路径来估值的，而对于一张地图，如果有了障碍，那么距离终点越远的地方，他可能遇到的障碍会越多。 预估距离是1000，实际距离可能是1300，预估距离是500，实际距离可能是650，而我们把已知距离和理论上的预估距离平等对待，相当于对未知地图预计太好。所以我们给预计距离加上一个系数。 公式成：

H(n) = sqrt(nMin *nMin *2) + nMax -nMin.

H(n) = 系数A * H(n) ;   // 这里的系数A大于等于1，这样才能如是反应实际距离。

上面的理论最优解系数相当于1.0 。 后面分别给出系数是1.5  2.0  3.0的结果：

 

    结论：启发式搜索的系数越大，搜索的速度越快（遍历的红色节点越少），但我们发现当系数等于3.0的时候，搜索的最优解是410，比真实的最优解408大了2个点。

     因为系数一旦超过1.0，那么刚才那么证明项就无法得出推导，所以答案可能不是最优。实际使用中，只能在精准性和速度上折中考虑。

再给一个相对普通的例子供参考：

分别是地图、 BFS搜索的结果，和启发式搜索（系数分别为1.0 2.0  3.0）

系数等于3.0速度虽然快，但距离多了26，系数取2.0结果正确，速度也不错。