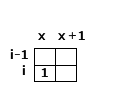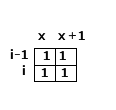算法练习系列—hiho1048 状态压缩一(铺地砖)
题目地址:http://hihocoder.com/problemset/problem/1048
编程之美的课后题也有一个和整个题目一样的。(P269)
题目
这个题目的题意很容易理解,在一个N*M的格子里,我们现在有两种类型的砖块,1 * 2和 2 * 1,问一共有多少种方案,可以将整个N*M的空间都填满。
最简单的例子就是下面的了:
编程之美中题目:
某年夏天,位于希格玛大厦四层的微软亚洲研究院对办公楼的天井进行了一次大规模的装修.原来的地板铺有 N×M 块正方形瓷砖,这些瓷砖都已经破损老化了,需要予以更新.装修工人们在前往商店选购新的瓷砖时,发现商店目前只供应长方形的瓷砖,现在的一块长方形瓷砖相当于原来的两块正方形瓷砖,工人们拿不定主意该买多少了,读者朋友们请帮忙分析一下:能否用1×2的瓷砖去覆盖 N×M 的地板呢?
下面我们来分析:
这个题目类属于状态压缩DP,对于状态压缩DP,其实最简单的理解就是把状态用比特位的形式表示出来,我们会在下面用例子来说明。
假如现在我们在铺砖 位置(i,j), 并且假设之前的位置已经铺设好的了,在这个位置,我们的选择:
1. 不用铺砖了,可能在(i-1, j)的时刻已经被竖着铺上了,然后考虑的是(i, j+1)
2. 横铺砖,将(i, j+1)也铺上了,然后考虑的是(i, j+2)。
3. 竖着铺砖,(将i,j)和(i+1,j)铺上一个竖立的转头。
所以我们如下翻译我们的选择,在位置(i, j) 如果我们选择横着贴砖,那么将(i, j), (i, j+1)都填写成1,如果竖着贴砖,我们将(i,j)填写成0,将(i+1, j)填写成1.
问题1:为什么要这么计数呢,我觉得应该这样理解:
1. 在横着贴砖的时候,(i, j), (i, j+1) 都是1,这个值其实对下一行如何选择没有影响。
2. 竖着贴砖的第二个,我们也选择了1, 因为这个砖头结束了,对下一行如何选择依然没有影响。
3. 而竖着的第一个砖头,这个砖头是对下面有影响的,如果(i,j)是0,那么(i+1,j)只有是1的情况下才能满足条件。
即当设为1表示对下一行没有任何影响了。
问题2:如何判断当前状态与上一行的状态是否兼容
其实我们在上面已经基本给出分析, 如果我们现在铺设 (i,x) x这里表示第i行,第x列
1. 如果值 i 行,j 在x位上的值是0, 那么第 i-1行,j的值在x位上一定是1。因为不可能在同一列相邻的位置铺两个竖着的 第一个,如果满足下一步测试的是(i, x+1), 否则直接返回不兼容。
2. 如果值 i 行,j在x位置的值是1 .
{
那么有可能有两种情况:
1. (i-1, x)是0, 这个时候一定是竖着铺设了,下一步检测的是(i, x + 1)
2. (i-1, x) 是1, 如果是这样的话,那么(i, x)一定是要选择横着铺了,那么(i,x+1)也一定是1,并且(i-1,x + 1)一定是1(如果是0,就是竖着铺了),如果不满足就返回不兼容,满足条件 就测试(i,x + 2)
图片
}
对于第一行的兼容性,我们要做一下特别的分析,在第一行中,要么放0, 要么放1。
加入当前测试的是 DP(0, j)的第 x的比特位,即第0行,x列
1. 如果x是1,那么 x + 1 也一定是1,然后测试到 x + 2
2. 如果x是0, 那么直接测试下一个 x + 1
特别注意:这里的判断的(i,x)一定不是由(i,x-1)位横着铺砖过来的,否则直接x=x+2,就不会来判断(i,x)位了。
问题3:为什么可以使用动态规划算法来解决这个问题?
这就得从动态规划的特性上去找:
(1)最优子结构
用F[i][j]表示第i行j状态铺砖块的方案数,一定等于i-1行所有的能与状态j兼容的状态k的方案的总和。
(2)重复子问题
求F[i][j]即第i行的每一个状态一定要用到第i-1行的各个状态。
问题4:从状态压缩的特点来看,这个算法适用的题目符合以下的条件:
1.解法需要保存一定的状态数据(表示一种状态的一个数据值),每个状态数据通常情况下是可以通过二进制来表示的。这就要求状态数据的每个单元只有两种状态,比如说棋盘上的格子,放棋子或者不放,或者是硬币的正反两面。这样用 0 或者 1 来表示状态数据的每个单元,而整个状态数据就是一个一串 0 和 1 组成的二进制数。
2.解法需要将状态数据实现为一个基本数据类型,比如 int, long等等,即所谓的状态压缩。状态压缩的目的一方面是缩小了数据存储的空间,另一方面是在状态对比和状态整体处理时能够提高效率。这样就要求状态数据中的单元个数不能太大,比如用 int 来表示一个状态的时候,状态的单元个数不能超过 32(32 位的机器)。
代码:
/*状态压缩DP******填充地板 http://hihocoder.com/contest/hiho9/problem/1 */
#include <iostream>
#include <algorithm>
#include <memory.h>
using namespace std;
#define NMax 1000
#define MMax 1<<5
bool testFirstLine(int j, int M) // 主要用来测试第一行的兼容性
{
int i = 0;
while(i < M)
{
if((j & (1<<i)) == 0) // 判断j的第i位是否为0 为1则执行 如果第i为1 则其前一位为0 如果判断的第j位为1 其后一位必然为0
i++;
else if(i == M-1 || !(j & (1 << (i+1))))
return false;
else i += 2;
}
return true;
}
bool testCompatible(int statesA, int statesB, int M) // 判断下一行状态stateA与上一行状态stateB的兼容性
{
int i = 0;
while(i < M)
{
if((statesA & (1<<i)) == 0)
{
if((statesB & (1<<i)) == 0)
{
return false;
}
i++;
}
else{
if((statesB & (1<<i)) == 0) i++;
else if(i == M-1 || !((statesA &(1<<(i+1))) && (statesB &(1<<(i+1)))))
{
return false;
}
else i += 2;
}
}
return true;
}
int main()
{
int N, M;
cin >> N >> M;
if(M > N){
swap(M, N);
}
int allStates = 1 << M;
long long F[NMax][MMax];
int i,j;
memset(F, 0, sizeof(F));
for(j = 0; j < allStates; j++)
{
if(testFirstLine(j, M))
{
F[0][j] = 1;
}
}
int k;
for(i = 1; i < N; i++)
{
for(j = 0; j < allStates; j++)
{
for(k = 0; k < allStates; k++)
{
if(testCompatible(j,k,M))
{
F[i][j] += F[i-1][k];
F[i][j] = F[i][j] % 1000000007;
}
}
}
}
cout << F[N-1][allStates-1]<< endl;
return 0;
}
/* 测试案例
2 4
5
*/
参考文献
1:http://blog.csdn.net/hopeztm/article/details/7841917 状态压缩动态规划 POJ2411 (编程之美-瓷砖覆盖地板)
2:http://www.myexception.cn/program/1612510.html