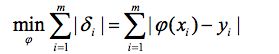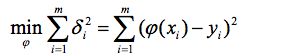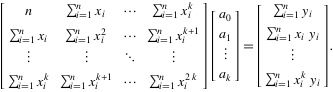数据拟合：多项式拟合polynomial curve fitting

http://blog.csdn.net/pipisorry/article/details/49804441

常见的曲线拟合方法

    1.使偏差绝对值之和最小

     

     2.使偏差绝对值最大的最小

     

     3.使偏差平方和最小

     

按偏差平方和最小的原则选取拟合曲线，并且采取二项式方程为拟合曲线的方法,称为最小二乘法。

皮皮blog

多项式拟合

多项式拟合公式

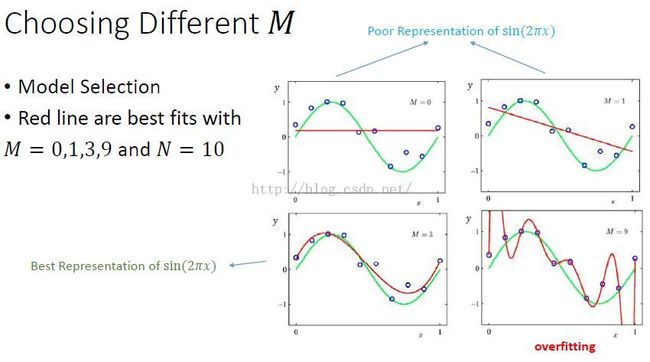
多项式阶数对数据拟合的影响

数据量较少，阶数过高，可能过拟合。

多项式拟合问题描述

假定给定一个训练数据集： T={(x1,y1),(x2,y2),⋯,(xN,yN)}

其中， xi∈R 是输入 x 的观测值， yi∈R 是相应的输出y的观测值， i=1,2,⋯,N ，多项式函数拟合的任务是假设给定数据由 M 次多项式函数生成，选择最有可能产生这些数据的 M 次多项式函数，即在 M 次多项式函数中选择一个对已知数据以及未知数据都有很好预测能力的函数。

设 M 次多项式为 fM(x,w)=w0+w1x+w2x2+⋯+wMxM=∑j=0Mwjxj ，式中 x 式单变量输入， w0,w1,⋯,wm 是 M+1 个参数。

参数W求解1

{实际上是一个最小二乘法多项式曲线拟合问题，根据给定的m个点,并不要求这条曲线精确地经过这些点，而是曲线y=f(x)的近似曲线y= φ(x)。}

用平方损失作为损失函数，系数 12 是为了方便计算，将模型与训练数据代入，有 L(w)=12∑i=1N(∑j=0Mwjxji−yi)2

对 wj 求偏导并令其为 0

set∂ L(w)∂wk=0⇒12∑i=1N2(∑j=0Mwjxji−yi)×xki=0⇒∑i=1N∑j=0Mwjxji＝∑i=1Nxkiyi(k=0,1,2,⋯,M)

所以要求拟合多项式系数 w∗0,w∗1,⋯,w∗M 需要解下面这个线性方程组，求和符号上下限都是 i=1 到 N 。

⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢N∑xi∑x2i⋮∑xMi∑xi∑x2i∑x3i⋮∑xM+1i∑x2i∑x3i∑x4i⋮∑xM+2i⋯⋯⋯⋱⋯∑xMi∑xM+1i∑xM+2i⋯∑x2Mi⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎛⎝⎜⎜⎜⎜⎜⎜⎜w0w1w2⋮wm⎞⎠⎟⎟⎟⎟⎟⎟⎟=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢∑yi∑xiyi∑x2iyi⋮∑xMiyi⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

所以计算出 ∑i=1Nxji(j=0,1,2,⋯,2M) 和 ∑i=1Nxjiyi(j=0,1,2,⋯,M) 然后将这些值带入上述线性方程组求解即可。

但是上面这个矩阵方程组求解是可以化简的：

参数求解2

{实际上是一个最小二乘法多项式曲线拟合问题，根据给定的m个点,并不要求这条曲线精确地经过这些点，而是曲线y=f(x)的近似曲线y= φ(x)。}

1. 设拟合多项式为：

          

2. 各点到这条曲线的距离之和，即偏差平方和如下：

          

3. 为了求得符合条件的a值，对等式右边求ai偏导数，因而我们得到了： 

          

          

                         .......

          

4. 将等式左边进行一下化简，然后应该可以得到下面的等式：

          

          

                     .......

          

5. 把这些等式表示成矩阵的形式，就可以得到下面的矩阵：

          

6. 将这个范德蒙得矩阵化简后可得到:

          

7. 也就是说X*A=Y，那么A = (X'*X)-1*X'*Y，便得到了系数矩阵A，同时，我们也就得到了拟合曲线。

这里的X就是6中方程左边的矩阵

皮皮blog

多项式拟合的python代码实现

{注意安装相关python库}

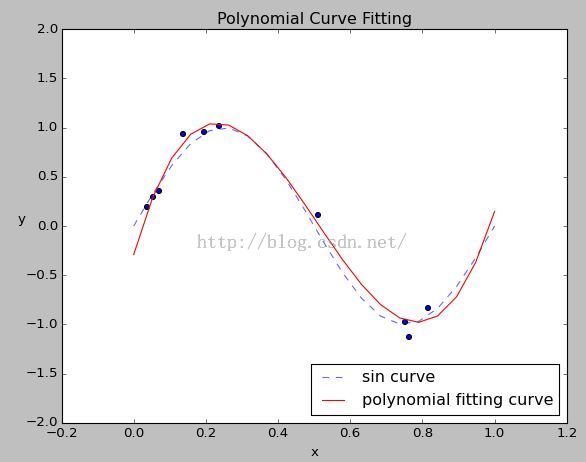
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
__title__ = '多项式曲线拟合'
__author__ = '皮'
__mtime__ = '11/8/2015-008'
__email__ = '[email protected]'
"""
import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg, stats

# 要拟合的函数
func = lambda x: np.sin(2 * np.pi * x)


def genPoints(p_no):
    '''
    获取要拟合的模拟数据
    '''
    x = np.random.rand(p_no)
    # x = np.linspace(0, 1, 10)
    # y要加上一个高斯分布N(0,0.01)随机偏差
    y = func(x) + stats.norm.rvs(loc=0, scale=0.1, size=10)
    return x, y


def drawCurveFitting(ax, w, x, y, order):
    '''
    绘制拟合曲线
    '''

    def drawSinCurve(ax):
        x = np.linspace(0, 1, 20)
        y = func(x)
        ax.plot(x, y, '--', alpha=0.6, label='sin curve')

    drawSinCurve(ax)

    def drawOriginData(ax, x, y):
        ax.scatter(x, y)

    drawOriginData(ax, x, y)

    def drawFittingCurve(ax, w, order):
        x = np.linspace(0, 1, 20)
        X = np.array([[xi ** i for i in range(order + 1)] for xi in x])
        y = X.dot(w)
        ax.plot(x, y, 'r', label='polynomial fitting curve')
        ax.set_ylim(-2, 2)

    drawFittingCurve(ax, w, order)

    def plotSetting(ax):
        ax.legend(loc='lower right')
        # plt.title('Polynomial Curve Fitting')
        # plt.xlabel('x')
        # plt.ylabel('y',rotation='horizontal')
        ax.set_title('Polynomial Curve Fitting')
        ax.set_xlabel('x', rotation='horizontal', lod=True)
        ax.set_ylabel('y', rotation='horizontal', lod=True)

    plotSetting(ax)

    plt.show()


def polynomialFit(x, y, order):
    X = np.array([[xi ** i for i in range(order + 1)] for xi in x])
    Y = np.array(y).reshape((-1, 1))
    # W = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(Y)
    W, _, _, _ = linalg.lstsq(X, Y)
    # print(W)
    return W


if __name__ == '__main__':
    order = 3  # 拟合多项式的阶数
    p_no = 10  # 拟合的数据点的个数

    ax = plt.subplot(111)
    x, y = genPoints(p_no)
    # print(x, '\n', y)

    W = polynomialFit(x, y, order=order)

    drawCurveFitting(ax, W, x, y, order=order)

运行结果

from:http://blog.csdn.net/pipisorry/article/details/49804441

ref:李航《统计学习方法》

多项式函数拟合问题V2

最小二乘法多项式曲线拟合原理与实现