数据科学之机器学习2：线性回归1

“文章原创，转载请注明出处”

一、回归分析

在统计分析中，最大的两支应该算是相关分析和回归分析。而回归分析应该是统计学的核心。回归分析，就是研究因变量 y 与自变量 x 之间的关系，存在条件数学期望： f(x)=E(y|x) 。此时有： y=f(x)+ε ，一般假设 ε∼N(0,σ2) 。

回归分析有很多变种：简单线性回归；多项式回归；Logistic回归；非参数回归；非线性回归等等。本篇就介绍最简单的线性回归，首先来看看一元线性回归。

二、一元线性回归

对于一元线性回归来说， f(x) 就是线性的，则有： f(x)=E(y|x)=β0+β1x 。通过已知的数据，可以估计出 β0,β1 的估计值： β^0,β^1 。那么就有 y 的预测值： y^=β^0+β^1x 。

1. 如何计算 β0,β1 的估计值 β^0,β^1 呢？

定义离差平方和：

Q(β0,β1)=∑i=1n(yi−f(xi))2

显然，我们希望 f(xi) 的值与真实值 yi 越接近越好。那么就是需要离差平方和越小越好。则得到目标：

minβ0,β1∑i=1n(yi−f(xi))2

如何寻找 β^0,β^1 使得上面方程达到最小呢？这个就需要对其对 β^0,β^1 求偏导，得到：

∂Q∂β0=−2∑i=1n(yi−β0−β1xi)

∂Q∂β1=−2∑i=1n(yi−β0−β1xi)xi

令上述两式都等于0，计算得到：

β^0=y¯−β^1x¯

β^1=∑ni=1(xi−x¯)(yi−x¯)∑ni=1(x−x¯)2

这样就得到 β0,β1 的估计值 β^0,β^1 。这个方法就叫做OLS，即普通最小二乘(ordinary least squares)。

2. R语言实现

在R语言中有自带的函数可以处理线性回归，那就是lm函数。这里使用自带的数据cars做演示：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

> attach(cars) # 使用数据集cars，与with函数类似 > lingre <- lm(dist ~ speed) > summary(lingre) Call: lm(formula = dist ~ speed) Residuals: Min 1Q Median 3Q Max -29.069 -9.525 -2.272 9.215 43.201 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -17.5791 6.7584 -2.601 0.0123 * speed 3.9324 0.4155 9.464 1.49e-12 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 15.38 on 48 degrees of freedom Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438 F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12 > plot(dist ~ speed, pch=4) # 画出散点图 > abline(lingre, col='red') # 添加拟合直线 > detach(cars) # 使用完记得释放

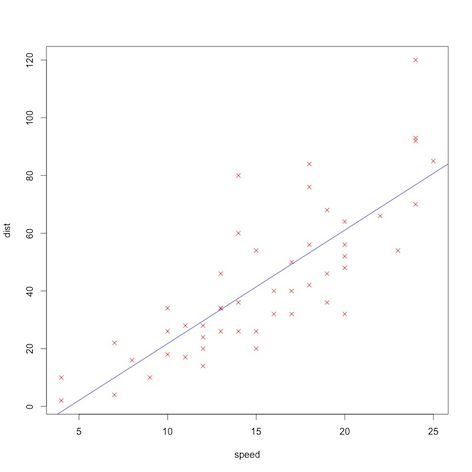
从这里可以得到回归方程： dist^=−17.5791+3.9324×speed 。（对于其它的结果是什么意思，可以去查看线性回归的相关书籍）

另外，得到拟合直线的图像：

三、多元线性回归

对于多元线性回归来说，其计算方式与一元线性回归类似，区别在于，多元的时候需要利用矩阵来处理。首先看一下回归模型：

y=β0+β1x1+β2x2+⋯+βpxp+ε

其中 p 代表自变量的个数。

若取 xT0=[1,1,…,1]1×n ，则可将上述模型改写成： y=Xβ+ε 。其中：

yT=[y1,y2,…,yn],X=[x0,x1,…,xp],βT=[β0,β1,…,βp],εT=[ε1,ε2,…,εn]

其中 xTi=[x1i,x2i,…,xni] 。

这样我们就可以将离差平方和 ∑ni=1(yi−β0+β1x1+β2x2+⋯+βpxp)2 写成矩阵形式：

(y−Xβ)T(y−Xβ)

求导可得： −2XT(y−Xβ) (这里用到矩阵求导的知识，一般介绍线性模型的书籍中会讲到；当然也可以直接对上面不是矩阵形式的离差平和求导)。令其等于0，可得：

β^=(XTX)−1XTy

R语言实现

对于R语言的实现，依旧使用lm函数：

1 2	lingre_mul <- lm(y ~ x1 + x2, data=datasets) summary(lingre_mul)

这里就不再用实际数据去演示了。

四、最后

至此，就把线性回归的基础内容介绍完了。但其实线性回归还存在很多其它的问题。比如说回归诊断（就是检查回归的效果），变量选择等等等等。感兴趣的话，可以找本讲线性回归的书看看，有很多！

转自：http://jackycode.github.io/blog/2014/03/30/machine-learning1/