Real-Time Rendering (6) - 多边形技术（Polygonl Techniques）

提要

       我们总是假设我们渲染的模型正是我们需要的，不论是细节上还是格式上，但实际上我们没那么幸运。建模工具和数据采集设备有着各自的缺点和局限，所生成的数据可能会有各种缺陷。

       图形学中呈现多边形的总体目的就是可视精度和速度。精确性是依具体情况而言的，对于机械而言，精确指的是模型的渲染在一定的误差范围；对于一个太空模拟游戏，最重要的是整体的感觉，模型的使用就成了关键。对于一个工程师，他希望每个斜角和倒角都显示清楚，对于游戏，只要足够流畅，一些小差错都是可以容忍的，因为它不一定出现在视线的焦点中，有些模型在下一帧或许就消失了。

      多边形技术中主要的几个技术是：细分（tesselation），合并（consolidation），优化（optimazation），简化（simplification）。多边形可以用很多其他的方式来表示，比如三角形，四边形，这样会让模型更好处理，这个过程称为三角划分或者曲面细分。consolidation指的是合并和关联多边形的数据，也包括生成新数据，比如生成法线；optimazation指的是对多边形数据进行细分，排序，使加快渲染速度。simplification指的是去除无关紧要或者无意义的细节。

     

3D数据源 Sources of Three-Dimentional Data 

       通常有下面几种获取3D数据的方法：

1.直接写出物体的数学描述；

2.通过程序生成模型数据（Pracedual modelling）；

3.将其他形式的数据转化为图形数据，如在信息可视化中将蛋白质数据转换成球或柱；

4.使用建模软件；

5.通过三维扫描仪生成点云，然后重建；

6.从多张图片中重建三维模型；

7综合使用上面的手段；

了解三维数据的来源对后面的处理非常重要。

主要有两种建模的思想：Solid-based和Surface-based.

Solid-based 方法通常用在CAD中，建模的工具盒现实中的很像，比如切刀，锉刀等等。在软件内部，会有一个计算引擎严格地管理着部件间的拓扑结构，在现实和分析方面，这种建模方式还需要一个切模刀（Faceter）。Faceter的能够做的是将模型从数学表示转化成一组多边形表示。比如一个球用数学表示就是空间中的一个点，再加上一个单值做半径就可以了。而Faceter要做的就是讲其转化为一组三角面片或者四边形面片。一个加速渲染的简单策略就是减少Faceter的精度来加速，减少Faceter生成的面数来减少存储空间。

需要考虑一个问题就是针对不同的目的，需要采用不同的Faceter，例如在FEM中，单元的划分就要尽量的均匀，方便计算。

       Surface-based 方法则没有solid的概念，所有的模型都是空心的壳，典型的3DMax和Blender中的建模都是这个方式。

      还有其他的建模方式，比如隐式曲面（implicit surface）创建系统，这种曲面的定义方式通常是定义一个三维的空间函数 f(x,y,z)=0, 压迫显示出来的话则要用到多边形化技术。

      还有很多其它方式，比如3D图像重建，3D扫描等，从这些数据中重建mesh会有一些难度，可以使用近年兴起的一些技术，比如PCL开源库。

      将表面生成多边形的技术可以用很多种，关键是找到方法还有要用作什么。

细分和三角化 Tessellation and Triangulation

       细分指的是将表面划分为一系列多边形，进行细分操作的原因有很多，比如几乎所有图形API和硬件都为三角行模型优化过，三角形就像是Mesh中的原子。将多边形模型中的所有多边形都转化为三角形称为三角化。另一个原因是有些渲染器或许要通过三角形来计算法线，得到光照等，还有些用于计算方面的要求，比如细分的三角形面积不能大于某个值，或者三角形的角不能小于某个值，又比如在有限元中，过于狭小的单元对于计算的结果很带来不良的影响。

合并 Cosolidation

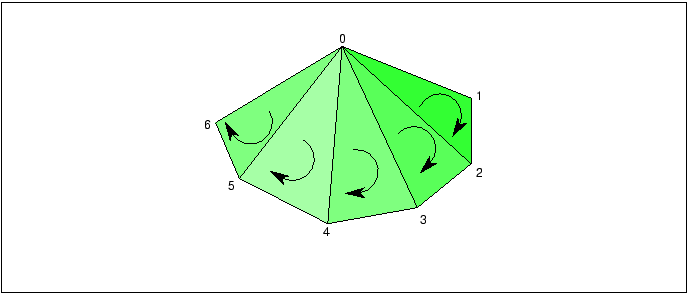
当一个模型经过Tessellation处理过后，剩下的就是一组待渲染的多边形了。可以用一些操作来优化显示数据，最简单的方法就是检测多边形是否正确，比如判断多变形最少包含三个点。还有就是找相同点进行合并，还有一个是朝向，多边形的点遵循右手法则，还有生成顶点法线，可以让表面看起来更加光滑。

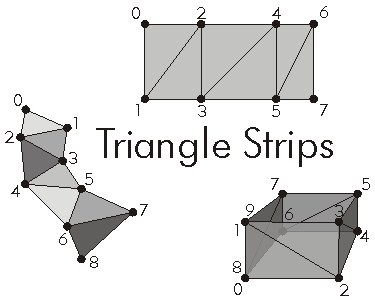
三角形扇，条，网格 Triangle Fans,Strips,Meshes

         一种加强图形表现的标准做法就是将一组三角形顶点数组传递到流水线中。好处是显而易见的：需要传递更少的顶点法线，需要计算更少的光照。

Fans

         用这种方式去表达一组三角形，平均下来每个三角形所需的顶点个数会少于三个。

            三角形是地形渲染中的基本图元，将一个凸多边形转换成三角形Fans会很繁琐，任何的三角Fans都可以转换为三角Strips，但反过来不行。

Strips 

       三角strip就像三角Fan，但三角Fans中中心点和上一个三角形的一个点的复用，而Strips中是用上一个三角形中的两个顶点来复用。

Creating Strips

       给定一个任意的三角网格，将其分解成三角Strips会很有用，获取最佳的三角Strips属于NP问题，我们可以用一种启发式的方法来逼近三角Strips的数量下界，比如贪心。

Triangle Meshes

       三角网格才是真正的数据共享，要尽可能地使用Triangle Meshes。

        一个闭合三角曲面平均每个三角形使用的顶点数为：

v-e+f+2g = 2  -- Euler-Poincare formula

        v为顶点的数量，e为边的数量，f是面的数量，g是物体中贯穿的空洞，一个球的g为0，一个圆环的g为1，一条边至少对应两个面，一个面至少有三条边，2e>=3f,代入得 f<=2v-4.如果所有面都是三角形，则2e=3f，得f=2v-4.

        当三角形的数量一定大的时候，f=2v,三角形的数量为面的两倍，则用Triangle Mesh的表达方式效率是Triangle strips的两倍。

顶点缓存 Vertex and  Buffers/Arrays

       在数据模型的加速存储方面，中最有效的方法是使用顶点buffer。

      基本思想是将模型数据存储于连续的内存块中，一个顶点buffer是用一定格式组织起来的顶点数据，格式知名一个顶点是否包含漫反射，范县，镜面反射，纹理坐标等等，一个顶点信息的字节数称为跨度。另一种是顶点流（Vertex stream）。实际上，单个的buffer包含所有顶点信息，在GPU中使用这种方法会更加高效。有时候会用到多流（multiple stream）.有时候，多流是跟好的选择，比如在不同光照下一匹马的模型，可以用不同表示光照条件的流合并上一个顶点流来得到想要的结果。

简化 Simplification

      mesh简化，也称为数据简化或者网格简化，目的是将一个复杂模型减少其多边形数量，同时爆出模型的外观，对于real time的渲染，这个过程主要是减少存储的顶点数并将其送入流水线，这样可以增加程序的可扩展性，老机器的性能是有限的，

      多边形简单的主要方式有三种：Static，Dynamic， View -dependent. 

参考

Real time rendering 3rd