Chord:一个用于网络应用的可扩展的P2P查询服务(上)
Chord:一个用于网络应用的可扩展的P2P查询服务
Ion Stoica*, Robert Morris, David Karger, M. Frans Kaashoek, Hari Balakrishnan
MIT Laboratory for Computer Science [email protected]
http://pdos.lcs.mit.edu/chord/
摘要
P2P(peer-to-peer)系统面临的一个根本问题就是如何有效的定位到存储特定数据项的节点。本文提出了Chord,一个分布式查询协议来解决这个问题。Chord专为一种操作提供支持:给定一个key,它将key映射到对应的节点上。基于Chord,通过把key和每个data item(数据项)关联起来,并把该key/data item对存储到key映射到的节点上,很容易就可以实现数据定位。Chord可以有效的适应节点加入、离开系统,并且可以在系统持续变动的状态下应答查询。理论分析、模拟和实验结果表明,Chord是一个可扩展的协议,并且通信代价和每个节点状态信息维护的代价都是系统中Chord节点个数的对数。
1 介绍
P2P系统和应用都是没有中心控制节点或者层次化组织结构的分布式系统,系统中的节点在功能上都是相同的。近来,许多P2P应用都具有冗余存储(redundant storage)、持久化(permanence)、临近服务器选择(selection of nearby servers)、匿名访问(anonymity)、搜索(search)、认证( authentication)和分级命名(hierarchical naming)等许多特征。然而绝大部分P2P系统中,最核心的操作是高效的数据定位。本文的贡献就在于提出了一个能为节点频繁加入、离开的动态P2P系统提供有效查询操作的可扩展协议。
【译注:数据定位(data location)、查询(query、lookup)都是一回事】
实际上Chord协议仅支持一种操作:把一个给定的key映射到一个节点(node)上。 依据基于Chord协议的应用而定,目标节点可能负责存储关联到key的一组数据。Chord使用了一致性hash算法[11](consistent hashing)的变体把Chord网络中的节点关联到特定而唯一的key上。一致性hash算法可以解决负载平衡(load balance)问题,因为它能保证系统中的每个节点都能接收到数量相当的key,并且当节点加入、离开系统时,减少数据的迁移。【译注:实际上一致性hash算法可以保证:当节点离开时,仅需要迁移离开节点上的数据;当节点加入时,仅将加入节点的后继节点的部分数据迁移到新节点上;而不涉及到其它的节点和数据,这在理论上已经是最小化的数据迁移了】
【译注:一致性hash算法的快速入门可以参见我的另一篇blog——一致性Hash算法 ,浅显易懂】
在以前对一致性hash算法的研究中,都假设每个节点都关注系统中的大多数节点,因此难以扩展应用到有很多节点的大规模系统中。相反,在Chord系统中,节点仅需要路由信息(routing information),关注少数其它节点。因为路由表是分布式的,一个节点执行查询时,需要和少数的其它节点通讯,稳定状态下,在一个有N个节点的系统中,每个节点仅需要维护O(logN)的节点信息,并且执行查询时仅需要和其它节点交互O(logN)的信息。当有节点加入、离开系统时,为了维护路由信息,Chord保证系统中节点之间的交互消息不会超过O(logN*logN)个。
Chord具有区别于其它P2P查找协议的3个特征:简单、正确性已经被证明和性能已经被证明。Chord简单有效,将key传递到目的节点仅需要路由O(logN)个节点。为了实现有效的路由,每个节点仅需要维护系统中O(logN)个节点的信息,并且在路由信息过期时,性能会优雅降级。这在实际中是很重要的,因为节点会随意的加入、离开系统,很难维持在O(logN) 的事件状态一致性。Chord协议中,每个节点仅有部分数据正确就能保证查询路由的正确性(尽管会变慢)。Chord具有简单的算法,能在动态的环境中维护路由信息。
文章其余部分的结构:第二节比较了Chord和其它的相关研究,第三节介绍了促进Chord协议的系统模型。第四节介绍了基本的Chord协议,并且证明了Chord协议的几个性质,第五节描述了能够处理多个节点同时加入、离开系统的扩展协议。第六节仿真和在实际部署的原型上的实验,论证了我们关于Chord性能的声明。最后,第七节列举了将来的工作,并在第八节总结了本文的成果。
2 相关工作
Chord将key映射到节点上,而传统的名字和定位协议提供从key到value的直接映射。value可能是地址、文档或者任意的数据项。Chord可以很容易的实现该功能,只需要把每个key/value对存储到由key映射到的节点上即可。因为这个原因并便于更明确的对比,本节的其它部分假设一个基于Chord、提供从key到value映射的服务。
DNS [15]提供从主机名到IP地址的映射,Chord也能提供相同的服务,以名字作为key,以IP地址作为关联到key上的value。Chord不需要专门的服务器,而DNS要依赖一组root域名服务器机。DNS域名是结构化的数据,以反映管理边界,Chord则没有命名结构。DNS是专门为查找命名主机或服务而设计的,而Chord还能用来查找没有绑定到特定主机的数据。
Freenet P2P存储系统 [4, 5],类似于Chord,具有去中心化、对称、节点加入和离开时的自适应性等特点。Freenet不会把文档权限分配到特定的服务器上,而是以查找缓存的副本的形式来实现查询。这使Freenet可以提供一定程度的匿名性(anonymity),但是也使Freenet不能保证一定可以获取(retrieval)到现有的文档或者保证获取操作的时间下限。Chord不提供匿名性,但是它的查询操作能在可预见的时间内完成,并且返回结果只有成功和确定失败两种情况。
Ohaha系统 采用了类一致性hash算法来把文档映射到节点上,和类Freenet风格的查询路由[18],因此它也具有Freenet的某些缺点。Archival Intermemory采用了离线计算树把逻辑地址映射到存储数据的节点上[3]。
Globe系统 [2]具有广域定位服务(wide-area location service),把物体标识符(identifier)映射到移动物体的位置上。Globe把因特网作为一个具有地理、拓扑或者管理域的层次关系组织起来,从而有效的构建了一个静态的世界范围的查找树,很像DNS。物体的信息被存储在一个特定的叶子域[12]【译注:leaf domain,翻译真别扭】中,指针缓存(pointer cache)提供了快捷的搜索路径。Globe通过使用类hash技术把物体划分到多个根物理服务器中,以达到在逻辑服务器上的高负载处理能力。Chord很好的实现了hash方法,因此可以在不引入任何层次结构的情况下达到可扩展性,Chord也没有像Globe一样利用网络位置信息。
由Plaxton等人开发的分布式数据定位协议 ,可能是与Chord最接近的算法,该协议的一个变体被应用于OceaStore中。它提供了比Chord更强的保证:和Chord一样,它保证查询能在对数级的跳数内完成,并且key的分布是平衡的,但是Plaxon协议还保证:以网络拓扑为准,查询所经过的网络距离,绝不会远于存储key的节点的距离。Chord的优势在于它更简单,并能更好的处理节点的并发加入、离开的情况。Chord还和PAST[8]中使用的定位算法Pastry相似,然而Pastry是一个基于前缀的路由算法,在其它细节方面也和Chord有所不同。
CAN 用一个d维的笛卡尔坐标空间(d是固定的)实现一个把key映射到value的分布式hash表。每一个节点维护O(d)的信息,查询复杂度为O(d*N^1/d)。因此,对比Chord,一个CAN网络中的节点维护的信息不依赖于网络规模N,而且查询复杂度增长速度比O(logN)高,如果d=logN,那么CAN的查询复杂度和信息维护的空间复杂度都和Chord相同。但是在CAN的设计中,d不能随着N而动态改变,因此这仅出现在当N恰好和d匹配时。CAN需要一个额外的维护协议以周期性的把key重新映射到节点中,Chord的另一个优势在于,当存在部分不正确的路由信息时仍具有健壮的正确性。
Chord的路由过程可以被看作是Grid定位系统[14](Grid location system)的一维模拟。Grid依赖于真实世界的地理位置信息来路由查询,Chord把节点映射到一个模拟的一维空间中,其中的路由被一个和Grid相似的算法来执行。
Chord可以被用作查询协议来实现不同的系统,就像第三节中所描述的那样。特别的,它可以用来预防Napster[17]中的单点故障(single points of failure)或控制,以及像Gnutella[10]那样广泛因使用广播(broadcast)而造成的缺乏扩展性。
3 系统模型
通过处理下面的这些难题,Chord简化了P2P系统和应用的设计:
负载均衡(Load balance) :Chord像一个分布式hash函数,最终将key散布在所有的节点上,这就在一定程度上提供了的天然的负载均衡能力。
去中心化(Decentralization) :Chord是完全分布式的,没有哪个节点是更重要的,这增强了健壮性,并使得Chord适合于松散组织的P2P应用。
可扩展性(Scalability) :Chord查询的复杂度随着节点数目N的log级别而增加(注:即O(logN)),因此适合应用在大规模系统中,并且不需要调整参数来达到这种可扩展性。
可用性(Availability) :Chord会自动调整内部表来反映新近加入节点和节点失效的情况,确保除了底层网络的严重失效外,负责key的节点总是可以查询到。这甚至在系统处于一个持续改变的状态时也是正确的。
灵活的命名规则(Flexible naming) :Chord对于要查找的key的结构没有施加任何的限制:Chord的key空间是扁平的(flat)。这就给应用程序与极大的灵活性来决定如何将他们自己的名字映射到Chord的key空间中。
Chord软件采取library的方式与使用它的客户端和服务端程序连接。应用程序和Chord主要在两个方面交互。1 Chord提供一个lookup(key)算法,返回负责key(存储key以及与key关联的数据)的节点的IP地址(注:即节点必要的信息)。2 每个节点上的Chord通知应用程序该节点所负责的key的变动。这允许应用程序执行一些操作,例如,在一个新节点加入时移动相应的数据到新节点上。
使用Chord的应用程序负责提供任何需要的认证、缓存、复制,和用户友好的数据命名。Chord的扁平key空间使得这些功能易于实现。比如一个程序可以验证数据d,这通过将d存储在一个来源于d的加密hash的Chord key下。类似的,应用程序可以复制数据d,这通过把d存储在两个不同的来源于d的应用层标识符的Chord key下。
下面就是一些Chord可以提供良好基础的应用例子:
协同镜像(Cooperative Mirroring) ,在一个近期的论文中描述[6]。设想有一组软件开发人员,每个人都希望可以提交发布。发布之间的需求可能差异巨大,从相当流行到不太流行【译注:这里看起来应该是影响的范围,有些发布可能影响很多人,有些发布影响范围比较小,原文:from very popular just after a new release to relatively unpopular between releases.】。一个有效的方法就是让开发人员之间相互镜像另一个人的发布。理想情况下,镜像系统可以提供服务器之间的负载平衡,复制、缓存数据,并且保证真实性。为了可靠性,这样一个系统应该完全的去中心化,而且也没有一个天然的中心管理组织。
时间共享存储(Time-Shared Storage) ,用于断续连接的节点。如果希望一些数据总是可用的,但是他们的机器只能是偶尔可用,那么当机器可用时,他们可以相互存储其它人的数据,反过来,他们的数据也存储在了另外的机器上【译注:这样当他们的机器不可用时,也可以从其它活动的机器上取得数据】。数据的名字可以用作key,在任何时候定位负责存储的(活动的)Chord节点。这里有很多问题和协同镜像应用是相同的,尽管这里的焦点是可用性而不是负载均衡。
分布式索引(Distributed Indexes) ,支持类似于Genutella或者Napster的关键字查询。本类应用中,key可能来自于要求的keyword,value可能是存储包含这些keyword的文档的机器列表。
大规模组合查询(Large-Scale Combinatorial Search) ,比如密码破解。这种情况下,key是问题(比如密钥)的候选解决方案;Chord把这些key映射到负责测试它们执行破解任务的机器上。
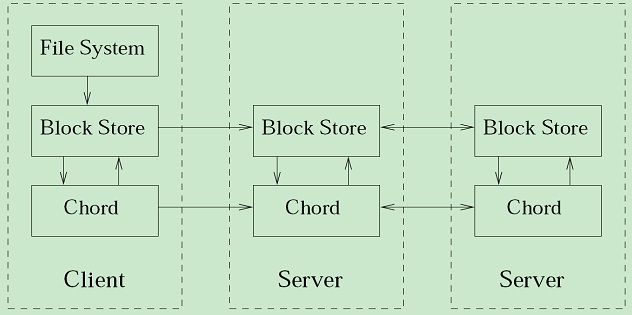
图1显示了协同镜像系统的一个可能的3层软件架构。最高层为用户提供一个类似文件系统的接口,包括用户友好的命名和认证机制。这个“文件系统”层可能实现命名文件夹和文件,并将对它们的操作映射到底层的块操作。下面一层是一个“块存储”层,实现需要的块操作。它负责块的存储、缓存和复制。“块存储”层将使用Chord来识别负责存储一个块的节点,然后联系节点上的块存储服务器来读写块。
4 基础Chord协议
Chord协议明确说明了如何查找key的位置,新节点如何加入到系统中,以及如何从节点失效中恢复。本节描述了一个没有处理并发的节点加入、失效的简化版协议。第五节描述了对该基础协议的增强来处理节点的并发加入和失效情况。
4.1 概述
Chord的核心就是提供了一个hash函数的快速的分布式计算,该hash函数把key映射到负责key的节点。Chord使用了一致性hash算法[11, 13],它具有几个很好的性质。该hash函数能在很大概率上实现平衡负载(所有的节点接收到大概相同数量的key)。并且在很大概率上,当一个节点加入(或离开)网络时,仅有一小部分key会被移动到另外的位置——显然这是为了维持负载平衡所需的最小移动了。
通过避免让每个节点知道其它所有节点的信息,Chord提高了一致性hash算法的可扩展性。在Chord网络中,每个节点仅需要知道包含少量其它节点的路由信息(routing information)。因为这个路由信息是分布式的,一个节点需要通过和少数其它节点通信来解答hash函数【译注:完成hash查询】。在一个具有N个节点的网络中,每个节点只需要维持O(logN)的节点信息,并且一次查询只需要O(logN)的交互信息。
Chord必须在节点加入、离开网络时更新路由信息,一次加入或离开更新需要O(logN*logN)的交互信息量。
4.2 一致性hash算法
一致性hash算法使用一个hash算法比如SHA-1[9]为每个节点和key分配一个m-bit的标识符。一个节点的标识符通过节点的IP地址的hash结果得到,而一个key的标识符通过hash这个key而得到。我们将使用术语key来同时指原始的key和hash后的结果,因为在上下文中它的含义是清晰的。相似的,术语“节点”也会同时指节点本身和节点hash后的标识符。标识符的长度必须足够长,以使得两个节点或key具有相同标识符的可能性可以忽略不计。
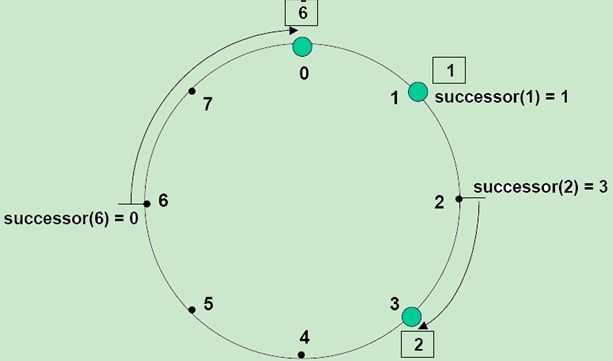
一致性hash算法采用如下的方式将key分配到节点上。标识符Identifier以Identifier mod 2^m【译注:mod为取模运算】的顺序排列到标识符环上。Key k被分派到标识符环上的第一个标识符等于或者紧随k(的标识符)的节点上。这个节点就是key k的后继(successor),记作successor(k)。如果标识符是从0到2^m-1的一圈数字,那么successor(k)就是在环上从k出发顺时针遇到的第一个节点。
图2是一个m=3的标识符环,上面有0、1、3这3个节点。标识符1的后继就是节点1,key 1将被定位到节点1上。同样的,key 2将被定位到节点3上,key 6将被定位到节点0上。
一致性hash算法设计的目的就是在节点加入、离开网络时做最小的数据分裂操作。为了维持正确的hash映射,在节点n加入网络时,最初分配给n的后继的key需要重新分配给n;当节点n离开网络时,n上所有的key将被分配给n的后继。除此之外不会再有key重新分配的情况。在上面的例子中,如果一个标识符为7的节点加入网络,那么标识符为6的key将被从节点0重分配到节点7上。
一致性hash算法的论文[11, 13] 证明了下面的结果:
定理1 对于任意N个节点和K个key的集合,在很大概率上(with high probability):
1 任何一个节点最多负责(1+cta)K/N个key;
2 当第N+1个节点加入或离开网络时,O(K/N)个key需要重新分配(并且仅是分配给加入的节点或从离开的节点上分配出去);
当一致性hash算法按照上面的描述实现时,定理可以保证cta=O(logN)。论文还证明了通过把每个节点以O(logN)个“虚拟节点”的方式运行,cta可以被降低到一个任意小值。
术语“很大概率上”需要一些讨论。一个简单的解释就是节点和key都是随机选择的,这在一个非对抗性的世界里貌似是可信的【译注:non-adversarial,看下面两句可理解】。概率分布是建立在随机选择的key和节点上的,因此这样的一个随机选择是不可能产生一个不平衡的分布的。然而,有人可能会担心,一个对手估计选择映射到相同标识符的key,来破坏其负载平衡的特性。一致性hash论文使用了“k-universal hash functions”来保证出现非随机选择的key的情况。
我们选择使用标准的SHA-1算法作为基本的hash算法,而不是使用“k-universal hash function”。这使得我们的协议是确定性的,因此“很大概率上”的声明也不再具有意义。但是使用SHA-1生成一组有冲突的key,或者破解SHA-1算法,被认为是极其困难的。因此,我们称协议具有“基于标准的强度假设”的性质(based on standard hardness assumptions),而不是“很大概率上”。
为了简单性,我们没有使用虚拟节点。在这种情况下,很大概率上(或者基于标准的强度假设)一个节点的负载可能会超出平均值一个系数。避免虚拟节点的一个原因是所需的虚拟节点个数由系统中的节点个数决定,而难以选择。当然,你可以在系统中选择使用一个预定义的虚拟节点上限,比如我们可以要求一个IPV4地址最多只能运行一个Chord服务,这样一个物理节点作为32个虚拟节点运行将会提供较好的负载平衡性。
4.3 可扩展的key定位
少量的路由信息有助于在一个分布式的环境中实现一致性hash算法。每个节点仅需关注它在环上的后继节点。一个给定标识符identifier的查询可以在环上沿着后继进行,直到第一次遇到identifier的后继,它就是要查询的节点。Chord协议维护了这些后继指针,以保证能正确的解决每次查询。然而,这种解决方法是低效的:它可能需要遍历所有的节点来找到合适的映射。为了加速查找,Chord还维护了额外的路由信息,这些额外的信息并非为了正确性,当然只要后继的信息是正确的,它们的正确性就能得到保证。
和前面一样,设key和节点的标识符都是m-bit的。每个节点维护一个有m项(最多)的路由表,又称为finger table。节点n的第i个表项存储了节点s,并且s是在标识符环上距离n至少为2^(i-1)的第一个节点,即s=successor(n+2^(i-1),其中1<= i <=m(所有的计算都基于模2^m)。我们称s为n的第i个finger,并标记为n.finger_t[i].node(见表1)【译注:为了不至于混淆finger和finger table,本文将原文中代表finger table的变量finger都改为finger_t】。finger table中的项包括相应节点的IP和端口信息。注意到节点n的第一个finger就是n在环上的后继,方便起见,我们经常称它为后继(successor)而不是第一个finger。
表1-1 节点n的变量定义(finger table在下表列出)
【译注:为避免混淆,本文将原文中的一个表分成了两个表项,并加上了说明列,做简单的必要补充说明】
如图3(b)中的例子所示,节点1的finger table将指向 (1 + 2^0) mod 2^3 = 2,(1 + 2^1) mod 2^3 = 3和(1 + 2^3) mod 2^3 = 5等3个标识符的后继。分别的,标识符2的后继是3,因为3节点紧跟标识符2的第一个节点,标识符3的后继是3,而标识符5的后继是0。
表1-2 节点的finger table表定义,对应于m-bit的标识符
【译注:根据定义,Finger table中的第一个finger,即第一个大于等于finger_t[1].start的节点,就是节点n的后继,n.successor = n.finger_t[1].node】
该模式有两个重要的性质:第一,每个节点只需存储少量的其它节点信息,并且在标识符环上,它知道的距离较近的节点比较远的节点更多;第二,一个节点的finger table通常并不包括足够的信息来确定任意key的后继。比如图3中的节点3并不知道标识符1的后继,因为1的后继(节点1)并不在节点3的finger table中。
如果一个节点n不知道key k的后继,它会怎么做呢?如果n能够找到一个标识符比自己更接近k的节点t,t将会比n知道更多的k区域的信息【译注:上面的性质1】。因此n查找它的finger table找一个标识符在k前面并且最接近k的节点j,并问j它知道谁的标识符更接近k。通过重复这个过程,n就会知道越来越接近k的节点。

图3 (a)节点1的finger区间 (b)节点0,1,3和key1,2,6,finger table和key位置
搜索的伪代码如图4所示【译注:代码中添加了响应的注释】。符号n.foo()表示函数foo()在节点n上执行。远程调用和变量引用前有远程节点标识,本地的调用和变量引用略去了本地节点标识。因此n.foo()代表了一个在节点n上的远程调用,而不带“()”的n.bar,则表示在节点n上查找变量bar的远程调用。
函数find_successor查找给定indentifier的直接前驱n,于是n的后继肯定也是identifier的后继。我们将实现函数find_predecessor,因为在后面的jion操作中也会用到(4.4小节)。
当节点n执行find_predecessor(id)时,它沿着Chord环上的一系列节点接近id。如果n联系到了节点n’,并且id落在了n’和n’的后继之间,find_predecessor将结束并返回n’。否则n询问n’知道的最接近id并在id之前的节点。因此算法将一直向着id的前驱执行。
比如,考虑图3(b)中的Chord环。假设节点3要查询标识符1的后继。因为1属于环形区间[7, 3),即3.finger_t[3].interval,因此节点3检查其finger table的第三项,就是0。因为0在1之前,节点3将向节点0查找1的后继。作为应答,节点0从推断出1的后继就是节点1本身,因此返回1给3。
// 委托节点n查找id的后继 n.find_successor(id) n’ = find_predecessor(id); // n的本地调用 return n’.successor; // RPC查询得到的n’的后继 // 委托节点n查找id的前驱 n.find_predecessor(id) n’ = n; // 这里查找的是前驱,id不能在n’中,因此区间是前开后闭 while(id NOT IN (n’, n’.successor]) // n’.successor由RPC查询得到 n' = n’. closed_preceding_finger(id); // n’上的RPC return n’; // 返回节点n的最接近id且在id之前的finger,都是本地调用 n.closed_preceding_finger(id) for i=m down to 1 // 从最大区间开始,每次迭代1/2递减 if(finger_t[i].node IN (n, id)) then // 落在区间内则找到 return finger_t[i].node; return n;
图4 查找伪代码
finger指针的倍增前进使(节点)和目标标识符的距离在find_predecessor中的每次迭代中减半。从这种直觉我们可以导出下面的定理:
定理2 在很大概率上(或者基于标准的强度假设),在一个N个节点的网络中,查找一个后继所需要联系的节点个数为O(logN)。
证明:假设节点n希望查询k的后继,且p是k的直接前驱结点,我们将分析到达p的步数。
回忆如果n != p,那么n将把查询转交给在finger table中最接近k的前驱。假设p在n的第i个finger区间中,因此该区间是非空的,n将在该区间找到节点f。节点n和f之间的(标识符)距离至少是2^(i-1)。但是f和p都在n的第i个finger区间中,因此n和f之间的距离最大是2^(i-1)。这意味着f距p比n近,或者说,从f到p的距离最多是从n到p的距离的二分之一。
如果在每次迭代时,接手查询的节点和p的前驱的距离以1/2递减,并且最初距离有2^m,那么在m步内距离将会减到1,意味着我们已经到达p。
实际上,像上面所讨论的,我们假设节点和key的标识符都是随机的,因此在很大概率上,查询的转交次数是O(logN),经过O(logN)转交之后,当前处理节点和key之间的距离将会降到2^m/N,我们期望落在该范围内的节点个数是1,很大概率上可能是O(logN)。
【译注:如果节点分布完全均衡,则2^m/N的范围仅含有一个节点,根据前面一致性hash的定理可知,有一个不均衡因子cta,在Chord的hash算法中,cta的取值很可能就是O(logN),在概率意义上节点间的距离最小可能是2^m/(N*O(logN)+1),因此在2^m/N的范围内可能会含有O(logN)个节点】
因此即使在剩下的步骤中每次只前进一个节点,遍历整个区间并达到key所需要的步骤数也在O(logN)之内。证毕
在第六节的实验结果报告中,我们将看到查询的平均时间是1/2logN。
4.4 节点加入
在动态网络中,节点可以在任何时候加入(离开)网络。实现这些操作的主要挑战就在于要保持网络根据key定位数据的能力,为了保持这种能力,Chord需要保证两个不变性:
1 每个node的后继都被正确的维护;
2 对于任意的key k,节点successor(k)是负责k的节点;
为了快速的查询,Chord也要求finger table是正确的。【译注:从后面可以看到,finger table并不总是正确的】
本节描述了如何在单个节点加入网路时如何维护这些不变性,我们将在第五节描述多个节点同时加入网络的情况,同时还描述了节点失效时的处理。在描述节点加入操作前,我们先总结它的性能(定理的证明参见合作技术报告[21]):
定理3 在很大概率上,节点加入、离开N各节点的网络时将需要O(logN*logN)的消息来重建Chord的路由不变性和finger table。
为了简化加入、离开机制,Chord中的每个节点都维护着一个predecessor指针,它包含节点直接前趋的Chord标识符和IP地址,因此可以逆时针的遍历标识符环。
为了保证上面声明的不变性,当节点n加入时Chord必需执行下面的3个任务:
1 初始化n的前驱结点指针predecessor和finger table
2 更新已存在节点的finger table和predecessor指针,以反映n的加入
3 通知上层软件,让它知道n的加入,以把n负责的状态(比如values)转移到n上
我们假设新节点通过一些外部机制可以获取一个Chord中的节点n’的标识符。节点n通过n’来初始化自己的状态信息,并且加入到Chord网络中,如下面所示的那样。
初始化predecessor和finger table:节点n请求n’在网络中查询它的predecessor和finger table,已完成初始化,使用的是init_finger_table,图6是它的伪代码。为finger table的m个表项依次执行find_successor来完成初始化,需要的时间是m*O(logN)。为了减少时间,对每个i,n都检查第i个finger是否和和第i+1个finger是相同的。这在finger_t[i].interval不包含任何节点时是成立的,因此finger_t[i].node >= finger_t[i+1].start。可以证明这个改进在很大概率上可以使需要执行查询的finger数目减少到O(logN),从而将总时间减少到O(logN*logN)。
一个实践上的优化,新加入的节点n可以请求复制一个邻居的完整finger table和predecessor指针。n可以使用这些表的内容给自己的finger table设置正确的值,因为n的表和它邻居的是相似的,可以证明这可以把设置finger table的时间减少到O(logN)。

图5(a) 节点6加入后,finger table和key位置的变化情况,变化部分用黑色标记
译注:为了便于对比,译文一并给出了前后两幅图
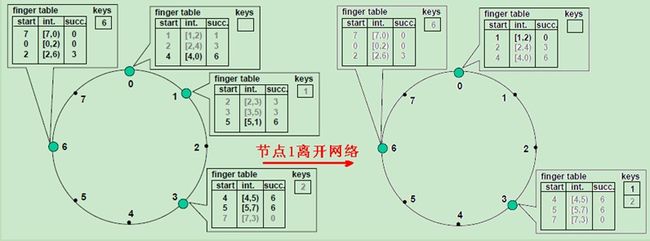
图5(b) 节点1离开后,finger table和key位置的变化情况,变化部分用黑色标记
译注:为了便于对比,译文一并给出了前后两幅图
#define successor finger_t[1].node // 节点n加入网络,n’是网络中的任意节点 n.join(n’) if(n’) init_finger_table(n’); update_others(); 把在(predecessor, n]中的key从successor中转移过来 else // n是网络中的唯一节点 for i=1 to m finger_t[i].node = n; predecessor = n; // 初始化本地节点n的finger table // n’是网络中的任意节点 n.init_finger_table(n’) finger_t[1].node=n’.find_successor(finger_t[1].start); predecessor = successor.predecessor; successor.predecessor = n; for i=1 to m-1 if(finger_t[i+1].start IN [n, finger_t[i].node)) finger_t[i+1].node = finger_t[i].node; else finger_t[i+1].node = n’.find_successor(finger_t[i+1].start); // 更新那些finger table应该指向n的节点 n.update_others() for i = 1 to m // 查找第i个finger是n的节点p p = find_precessor(n – 2^(i-1)); p.update_finger_table(n, i); // 如果s是n的第i个finger,更新其finger table n.update_finger_table(s, i) if(s IN [n, finger_t[i].node)) finger_t[i].node = s; // 获取n的直接前驱p p = predecessor; // 递归更新 // 可能需要将p的第i个finger更新为s // 因为s也可能在[p, p.finger_t[i].node)区间 p.update_finger_table(s, i);
图6 节点加入操作的伪代码
更新已存在节点的finger:节点n需要加入到一些已存在节点的finger table中,比如在图5(a)中,节点6成为节点0和1的第三个finger,成为节点3的第一和第二个finger。
图6描述了更新已有finger table的update_finger_table函数的伪代码。节点n将成为节点p的第i个finger,当且仅当:(1)p在n前至少2^(i-1)的距离,(2)p的第i个finger在n的后面。
【译注:n=p.finger_t[i].node >= finger_t[i].start = (p+2^(i-1)) mod 2^m => n >= (p+2^(i-1)) mod 2^m;因为n更靠前,于是需要更新p的第i个finger】
能够满足上面两个条件的节点p是n-2^(i-1) mod 2^m的直接前驱。因此给定n,算法从n的第i个finger开始,然后逆时针方向遍历环,直到遇到一个第i个finger在n前面的节点。
我们在技术报告[21]中证明了,在很大概率上,当节点加入到网络时需要更新的节点个数是O(logN)。查找和更新这些节点需要的时间是O(logN*logN)。一个更复杂的机制可以把时间减少到O(logN);然而,我们不准备描述它,因为我们将在后面的章节中使用该算法。
Key的转移:n加入网络时最后需要执行的一个操作就是把所有后继为n的key转移到n上。毫无疑问,细节取决于基于Chord的上层应用程序,但是典型的操作将会涉及到把这些key关联的数据转移到新节点n上。节点n仅仅会成为原先被紧接着n的节点【译注:n的后继】负责的部分key的后继,因此n只需要联系它并把相应的key转移过来就行了。