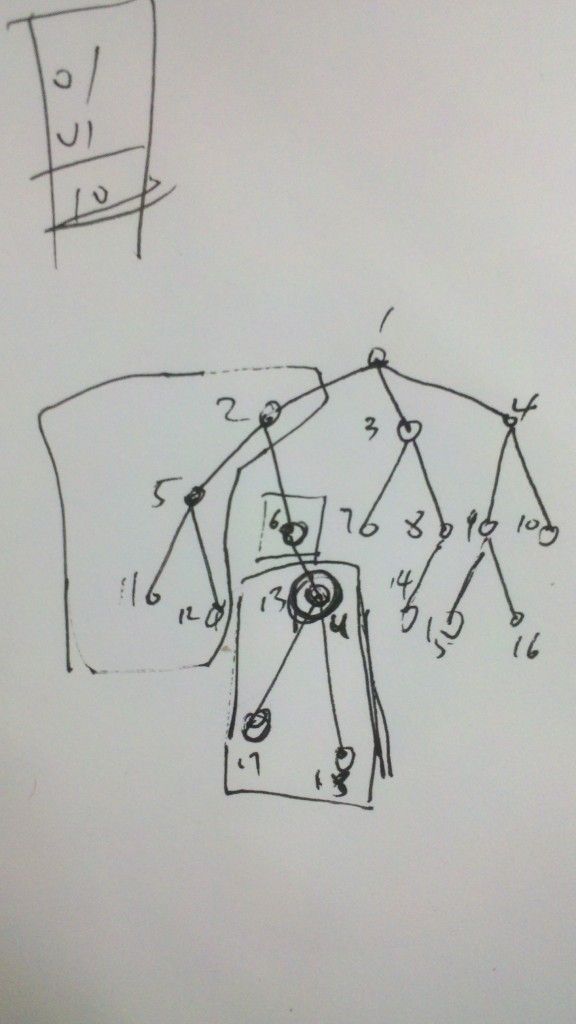
lca---tarjan算法

上面是个草图，特别草

假设现在u = 13号结点，此时按照tarjan算法，2,5,11,12结点作为一类，但是此类的标签不一定是2，所以必须用单独的ancestor指定此类的根结点是2；6号结点单独作为一类，13,17,18作为一类，其他结点都是各自作为一类，如果要求13和11的最近公共结点，只要求11所在类的根结点，即2，以此根结点作为最近公共结点；同理，13与2,5,11,12的最近公共结点都是2(但是现在还不能求出13和2的公共节点，因为2的所有分支还没有遍历完)；但是现在还求不出来13和6的公共结点，因为这时vist[6] = 0,所以还不能求；当算法继续运行，回溯至6结点，此时6,13,17,18作为一类，这个类的根结点是6，所以此时就可以求6和13的最近公共结点，就是求出13的根结点（因为这时vist[13] = 1），也就是6;

tarjan算法可以看做后序遍历，只有当前节点u的所有分支都访问完之后，才将vist[u] = 1,表示u已经访问过了。

依次访问当前节点u的所有孩子节点，访问完一个就把这个分支的节点和节点u标注为一类，并且注明这个类的代表就是u;这样依次把u的孩子节点并入以u为代表的类中。

要注意，虽然把u和其孩子节点并入一类，但是在访问完u的所有孩子之前，u还是没有被访问过的。

设当前节点是13, 则13和6的lca不可求，这是因为6的孩子节点还没有访问完，6还是未访问的。

下面是poj1330的代码:

#include <vector>
#include <stdio.h>
#include <cstring>
#include <iostream>
using namespace std;

const int MaxNode = 10001;
vector<int> g[MaxNode];
vector<int> q[MaxNode];//用来记录query

int f[MaxNode];
int r[MaxNode];//rank
int indegree[MaxNode];
int ancestor[MaxNode];
bool vist[MaxNode];

void Init(int n)
{
	for (int i=1;i<=n;++i)
	{
		f[i] = i;//各自为类
		r[i] = 1;
		g[i].clear();
		q[i].clear();
	}
}

void Merge(int a,int b)
{
	int pa = f[a];
	int pb = f[b];

	if (pa!=pb)
	{
		if (r[pa]>r[pb])
		{
			f[pb] = pa;
		}
		else//将pa的father变为pb
		{
			f[pa] = pb;
			if (r[pa] == r[pb])
			{//pb的rank增大
				++r[pb];
			}
		}
	}
}

int Find(int a)
{
	if(a!=f[a])
		f[a] = Find(f[a]);

	return f[a];
}

void Tarjan(int u)
{
	ancestor[u] = u;
	for (int i=0;i<g[u].size();++i)
	{
		Tarjan(g[u][i]);
		Merge(u,g[u][i]);
		ancestor[Find(u)] = u;//merge之后，类别标签改变，但是必须保证这个类的根节点是u

	}

	vist[u] = true;//每当一个节点的所有分支都遍历结束时，就检查与这个节点相连的查询节点
	for (int i=0;i<q[u].size();++i)
	{
		if(vist[q[u][i]])
		{
			cout<<ancestor[Find(q[u][i])]<<endl;
			return;
		}
	}

}

int main()
{
	int Case;
	scanf("%d",&Case);
	int ind = 0;
	for (;ind<Case;++ind)
	{
		int count;
		scanf("%d",&count);
		Init(count);
		memset(indegree,0,sizeof(indegree));
		memset(ancestor,0,sizeof(ancestor));
		memset(vist,0,sizeof(vist));
		int u,v;
		for (int i=0;i<count -1;++i)
		{
			scanf("%d%d",&u,&v);
			g[u].push_back(v);
			++indegree[v];
		}
		scanf("%d%d",&u,&v);
		q[u].push_back(v);
		q[v].push_back(u);

		for (int i=1;i<=count;++i)
		{
			if (indegree[i] ==0)//找到树的根节点
			{
				Tarjan(i);
			}
		}

	}
	return 0;
}

Tarjan算法虽然简单，但是很少有资料说的清楚的，下面一段话摘自：http://dongxicheng.org/structure/lca-rmq/

Tarjan算法也要用到深度优先搜索，算法大体流程如下：对于新搜索到的一个结点，首先创建由这个结点构成的集合，再对当前结点的每一个子树进行搜索，每搜索完一棵子树，则可确定子树内的LCA询问都已解决。其他的LCA询问的结果必然在这个子树之外，这时把子树所形成的集合与当前结点的集合合并，并将当前结点设为这个集合的祖先。之后继续搜索下一棵子树，直到当前结点的所有子树搜索完。这时把当前结点也设为已被检查过的，同时可以处理有关当前结点的LCA询问，如果有一个从当前结点到结点v的询问，且v已被检查过，则由于进行的是深度优先搜索，当前结点与v的最近公共祖先一定还没有被检查，而这个最近公共祖先的包涵v的子树一定已经搜索过了，那么这个最近公共祖先一定是v所在集合的祖先。