排序算法--交换排序之快速排序

一、目的：  减少总的比较次数和移动次数，增大记录的比较和移动距离，较大记录从前面直接移到后面，较小记录从后面直接移动前面。

二、主要思想：        

首先选一个周值（即比较的基准），通过一趟排序将待排序记录分割成独立的两部分，前一部门记录的关键值均小于或者大于轴值，后一部门记录的关键码均大于或等于轴值，然后分别对这两部分重复上述方法。直到整个序列有序。

三、主要问题

（1）如何选择轴值？

  A 使用第一个记录的关键码

  B 选取序列中间记录的关键码

  C取关键码居中的作为轴值并调换到第一个记录的位置

  D随机选取轴值

选取不同轴值的后果

决定两个子序列的长度，子序列的长度最好相等。

（2）如何实现分割（称一次划分）？

 解决办法：

      设置待划分的序列是r[s] -- r[t],设参数i,j 分别指向子序列左\右两端的下标s和t,令r[s]为轴值

     A， j 从后向前扫描，直到r[j] > r[i] ,将r[j]移到r[i]的位置，使关键码小(同轴值相比)移动到前面去。

    B i从前往后扫描，直到r[i] > r[j]， 将r[i]移动到r[j]的位置，使关键码大的移动到后面去。

    C 重复上面，直到i = j;

如下图所示： 

算法描述

int Partition(int r[ ], int first, int end)
{	
    i=first; j=end;         //初始化
    while (i<j)	
    {  
       while (i<j && r[i]<= r[j]) j--；  //右侧扫描
       if (i>j) { 
          r[i]←→r[j];   i++;  //将较小记录交换到前面
       }
       while (i<j && r[i]<= r[j]) i++；  //左侧扫描
       if (i>j) {
          r[j]←→r[i];   j--;  //将较大记录交换到后面
       }
    }
    retutn i;    //i为轴值记录的最终位置
}

（3）如何处理分割得到的两个待排序子序列？

      对分割得到的两个子序列递归的调用快速排序。

     算法描述

void QuickSort (int  r[ ], int first, int end )
{
    pivotpos = Partition (r, first, end );  //一次划分  
    QuickSort (r, first, pivotpos-1);      
                             //对前一个子序列进行快速排序
    QuickSort (r, pivotpos+1, end ); 
                             //对后一个子序列进行快速排序
}

（4）如何判断快速排序的结果

解决方法：

若待排序列中只有一个记录，显然已有序，否则进行一次划分后，再分别对分割所得的两个子序列进行快速排序（即递归处理）。

  算法描述

void QuickSort (int  r[ ], int first, int end )
{//在序列 first~end中递归地进行快速排序
    if (first < end) {					
          pivotpos = Partition (r, first, end );    
          QuickSort (r, first, pivotpos-1);
          QuickSort (r, pivotpos+1, end );
   }
}

三、性能分析

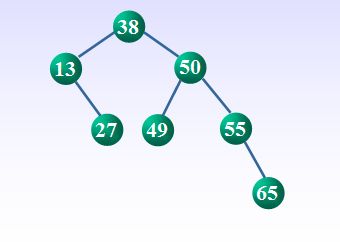
快速排序的递归执行过程可以用递归树来表示，所形成的是一个二叉树。例如：

例：{38, 27, 55, 50, 13, 49, 65}的快速排序递归树如下：

最好情况：

每一次划分对一个记录定位后，该记录的左侧子表与右侧子表的长度相同，为O(nlog2n)。

最坏情况：

每次划分只得到一个比上一次划分少一个记录的子序列（另一个子序列为空），为 O( n2)。

平均情况：为 O( nlog2 n)。