trie图的构建------易理解版

当然看这篇文章最好在看trie图那篇原文看不懂的情况下再看这篇

这篇只是便于理解可能有不严谨的地方

看trie图看了一个小时终于看明白了，冯涛原创，我在网上就看到有一篇讲解trie图的看的好费劲啊，绕圈子都快拧成死疙瘩了，我根据自己理解的捋一捋：

首先，要建立好一个trie树

Trie树的建立：

       前提：结点定义有一个标志位表示结点是否是危险结点，有一个指针数组保存所指向的儿子结点

          

</pre><pre name="code" class="cpp">struct   trie_node
{
     int  d;//标志位
     trie_node *child[MAX];
};

       第一，首先初始化一个根节点

          第二，读入字符x，若当前结点的child[x-'a']不为空则把当前结点设置为child[x-'a'];若当前结点的child[x-'a']为空，则新初始化一个结点作为child[x-'a']然后把当前结点设置为child[x-'a']。若字符x为单词的最后一个字符设置当前结点的标志位。

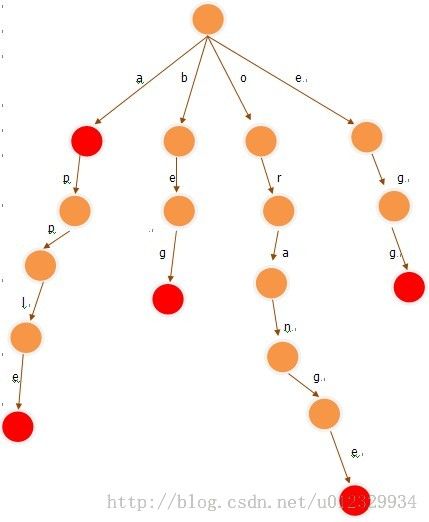
例如：有以下五个单词：

a

apple

beg

orange

egg

那么建立的trie树为：

然后，将其改造成trie图

那么在改造trie图的时候：

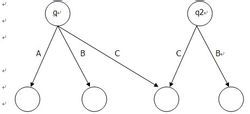
首先，第一步就是求出所有结点的后缀结点（后缀结点的求法原文中比较绕）

查找每个节点的后缀结点

层序遍历Trie树的每个结点：

对于根节点root的后缀结点是根节点root本身；

对于根节点root的儿子结点，即根节点的下层结点，它们的后缀结点是根节点root；

对于其余的结点的后缀结点的查找：

设当前结点为q，结点q的父结点为结点p，结点p指向结点q的边上的字符为‘A’，结点p的后缀结点是结点p2。那么结点q的后缀结点就是结点p2沿标有字符'A'的边走一步后到达的结点。

注意： 如果结点p2没有字符为‘A’的边，那么这个时候就找结点p2的后缀结点p3，如果结点p3有字符为‘A’的 边， 那么结点p3沿标有字符'A'的边走一步后到达的结点就是结点q的后缀结点。如果结点p3也没有字符为'A'的边，那么就找结点p3的后缀结点p4直到根节点root， 直到结点root，结点root也没有字符为'A'的边,那么结点q的后缀就设置为结点root。

 

                        

                     

 

 

 

然后，有了后缀结点就可以对每一个结点进行拓展了也就是建立新的边

连接新边

在找到后缀结点后，同时对当前结点q进行新边的连接。设结点q的后缀结点为结点q2。那么需要连接的新边就是结点q2存在而结点q没有的边，那么结点q就新建一条边指向结点q2所指向的结点。例如：结点q有两个儿子结点：结点q通过边‘A’指向一个儿子结点；结点q通过边'B'指向一个儿子结点。结点q2有两个儿子结点：结点q2通过边‘C’指向结点e；结点q2通过边'B'指向结点f。那么这时就需要结点q新建一条边‘C’指向结点e，结点q2不做任何修改。

                                                        

 

扩展新边后：

                

 

 

 

                                                                                                    

                 

 

 

以结点p为根的子树与以结点p的后缀结点为根的子树是一样的.其实这只是讲了建立的过程对于其中深奥的含义还得细细品味