求二部图的最小覆盖顶点

1. 最小覆盖顶点

http://www.matrix67.com/blog/archives/116

2. 代码

/*
This is a free Program, You can modify or redistribute it under the terms of GNU
*Description:输入一个图,能够识别该图是不是二部图,如果是,自动将此二部图的顶点划分为
红点集合蓝点集,并确保红点集中元素个数小于等于蓝点集中元素的个数,
此系统核心功能还包括找出二部图最大匹配,完备匹配,最优匹配,最小覆盖顶点集(Konig)
*Language: C++
*Development Environment: VC6.0
*Author: Wangzhicheng
*E-mail: [email protected]
*Date: 2012/10/23
*/

#include "graph.h"
#include "graph.cpp"
#include <string>
#include <vector>
#include <map>
#include <stack>
#include <set>
using namespace std;

enum Color{red,blue,black};  //定义颜色

/*
二部图类,是图的公有派生类
*/
template<class ElemType>
class Bipartite_Graph:public Graph<ElemType> {
	private:
		bool flag;				//表示此图是不是二分图
		bool isolateflag;       //表示此图是否有孤立点
		bool perfectMatch;      //表示此图有没有完备匹配
		vector<int>Red;			//红点集向量
		vector<int>Blue;		//蓝点集向量
		vector<int>unMatchBlue; //蓝点集中未匹配的点  
		vector<int>isolate;     //孤立点集合 
		Color *vertexcolor;		//颜色向量,向量中每个元素为相应顶点的颜色
		map<int,int>match;		//<蓝点,与蓝点匹配的红点>
		set<int>MarkedRed;   //打上标记的红点集
		set<int>MarkedBlue;  //打上标记的蓝点集
		set<int>minCoveredPoints; //最小覆盖顶点集
		int count;				//此二部图的匹配数
        /*********************************************************/
		stack<pair<int,int> >Stack;  //保存着匹配
		stack<pair<int,int> >tempStack;  //临时保存Stack内容
		vector<pair<stack<pair<int,int> >,int> >MatchArray;  //存放所有匹配和其对应的权值和的向量

	public:
		/*
		二部图的构造方法,在构造方法中,完成识别二部图的功能,划分出红点集合蓝点集的功能
		*/
		Bipartite_Graph(bool IsDirect,bool IsWeight):Graph<ElemType>(IsDirect,IsWeight) {
			vertexcolor=new Color[graph.vertexnum];
			isolateflag=false;
			flag=true;
			perfectMatch=true;
			count=0;
			int i,j;
			for(i=0;i<graph.vertexnum;i++) vertexcolor[i]=black; //将所有顶点都打上黑色
			for(i=0;i<graph.vertexnum;i++) visited[i]=false;  //将所有顶点都设置为未访问
			for(i=0;i<graph.vertexnum;i++) {
				if(visited[i]==false) {
					IsBipartite_Graph_DFS(i,red);  //判断输入的图是不是二部图,如果是,则将图的顶点划分为红点集和蓝点集
					if(flag==false) return;  //IsBipartite_Graph_DFS执行后,如果输入的图不是二部图,则flag==false
				}
			}
			Exchange();  //如果需要,交换红点集合蓝点集
			count=0;
			vector<int>::iterator it;
			/*
			初始化时,将每个匹配设置为<蓝点,-1>,即蓝点对应的红点为-1
			*/
			for(it=Blue.begin();it!=Blue.end();it++) {
				pair<int,int>p(*it,-1); // <蓝点,-1>
				match.insert(p);
			}
			
		}
		/*
		最大匹配算法
		*/
		void MaxMatch() {
			vector<int>::iterator it;
			if(flag==false) {
				cerr<<"不是二部图!"<<endl;
				return;
			}
			for(it=Red.begin();it!=Red.end();it++) {
				/*
				每次到蓝点集中找增广路径之前,都将所有蓝点设为为未访问
				这样才能找到最大匹配
				*/
				for(int i=0;i<graph.vertexnum;i++) visited[i]=false;
					if(DFS(*it)) count++;
			}
			ElemType red,blue;
			cout<<"最大匹配是:"<<endl;
			map<int,int>::iterator pos;
			for(pos=match.begin();pos!=match.end();pos++) {
				if(pos->first==-1 || pos->second==-1) {
					unMatchBlue.push_back(pos->first);
					continue;  //此时match中有顶点没有匹配
				}
				Get(pos->first,blue);  
				Get(pos->second,red);  
				cout<<"红点:"<<red<<"到"<<"蓝点"<<blue<<endl;
			}
			cout<<"共有"<<count<<"个匹配"<<endl;
			cout<<"未匹配的蓝点是:";
			for(it=unMatchBlue.begin();it!=unMatchBlue.end();it++) {
				cout<<*it<<" ";
			}
			cout<<endl;
		}

		/*
		匈牙利算法,其核心思想是对于红点集中每一个红点,到蓝点集中找出所有的增广路径,找到就增广
		从而不断扩充原有的匹配,如果红点集中每个红点都找到匹配,即其所对应的蓝点,则程序找到
		完备匹配
		*/
		void Hungary() {  
			vector<int>::iterator it;
			if(isolateflag==true || flag==false)  {
				if(flag==false) {
					cerr<<"不是二部图!"<<endl;
					return;
				}
				else {
					cerr<<"此二部图存在孤立点,找不到最优匹配!"<<endl;
					return;
				}
			}

			for(it=Red.begin();it!=Red.end();it++) {
				/*
				每次到蓝点集中找增广路径之前,都将所有蓝点设为为未访问
				这样才能找到完备匹配
				*/
				for(int i=0;i<graph.vertexnum;i++) visited[i]=false;
					if(DFS(*it)) count++;
			}
			if(count<Red.size()) {  //此时至少有一个红点没有与其匹配的蓝点
				cerr<<"此二部图不存在完备匹配!"<<endl;
				perfectMatch=false;
				return;
			}
			ElemType red,blue;
			cout<<"完备匹配是:"<<endl;
			map<int,int>::iterator pos;
			for(pos=match.begin();pos!=match.end();pos++) {
				if(pos->first==-1 || pos->second==-1) continue;  //此时match中有顶点没有匹配
				Get(pos->first,blue);  
				Get(pos->second,red);  
				cout<<"红点:"<<red<<"到"<<"蓝点"<<blue<<endl;
			}
			cout<<"共有"<<count<<"个匹配"<<endl;
		}
		/*
		显示二部图的红点集合蓝点集
		*/
		void show() {
			Graph<ElemType>::show();
			vector<int>::iterator it;
			cout<<endl<<"红点集是:"<<endl;
			for(it=Red.begin();it!=Red.end();it++) {
				cout<<*it<<" ";
			}
			cout<<endl;
			cout<<endl<<"蓝点集是:"<<endl;
			for(it=Blue.begin();it!=Blue.end();it++) {
				cout<<*it<<" ";
			}
			cout<<endl;
			if(isolateflag) {
				cout<<endl<<"孤立点是:"<<endl;
				for(it=isolate.begin();it!=isolate.end();it++) {
					cout<<*it<<" ";
				}
			}
			cout<<endl;
		}
		~Bipartite_Graph() {
			delete []vertexcolor;
		}
	/**********************************************************************/
		/*
		此方法找出最优匹配,核心思想是利用枚举法,当某个红点i在蓝点集中找到匹配时,
		下一个红点i+1从未访问过的蓝点中找匹配
		*/
		void OptimalMatch() {
			int i,k;
			if(isolateflag==true || flag==false)  {
				if(flag==false) {
					cerr<<"不是二部图!"<<endl;
					return;
				}
				else {
					cerr<<"此二部图存在孤立点,找不到最优匹配!"<<endl;
					return;
				}
			}
			for(i=0;i<graph.vertexnum;i++) visited[i]=false;
			k=0;  //k表示匹配数
			perfectMatch=false;
			vector<int>::iterator it=Red.begin();
			DFS(it,k);
			if(perfectMatch==false) {
				cerr<<"该二部图不存在完备匹配!"<<endl;
				return;
			}
			int maxpos;
			int maxweight=0;
			for(i=0;i<MatchArray.size();i++) {
				if(MatchArray[i].second>maxweight) {
					maxweight=MatchArray[i].second;
					maxpos=i;
				}
			}
			cout<<"最优匹配是:"<<endl;
			stack<pair<int,int> > s=MatchArray[maxpos].first;
			while(s.empty()==false) {
				int red=s.top().first;
				int blue=s.top().second;
				cout<<"红点:"<<red<<"--"<<"蓝点:"<<blue<<endl;
				s.pop();
			}
			cout<<"权值和为:"<<maxweight<<endl;
		}
		/*
		*最小覆盖点集
		*/
		void MinCoveredPoints() {
			vector<int>::iterator it;
			int i; //指向蓝点
			int j; //指向红点
			for(it=unMatchBlue.begin();it!=unMatchBlue.end();it++) {
				setVisitedFalse();
				i=*it;
				while(true) {
					MarkedBlue.insert(i);  //将蓝点加入标记集合
					visited[i]=true;
					j=BlueToRed(i);          //找到与蓝点i相邻接且未匹配的红点
					if(j==-1) break;
					MarkedRed.insert(j);  //将红点加入标记集合
					visited[j]=true;
					i=MatchedRed(j);		 //找到与红点j匹配的蓝点i
				}
			}
			set<int>::iterator pos;
			for(pos=MarkedRed.begin();pos!=MarkedRed.end();pos++) {
				minCoveredPoints.insert(*pos);
			}
			for(it=Blue.begin();it!=Blue.end();it++) {
				if(MarkedBlue.find(*it)==MarkedBlue.end()) minCoveredPoints.insert(*it);
			}
			cout<<"最小覆盖顶点是"<<endl;
			ElemType e;
			for(pos=minCoveredPoints.begin();pos!=minCoveredPoints.end();pos++) {
				Get(*pos,e);  
				cout<<e<<" ";
			}
			cout<<endl;
		}
	private:
		void Exchange() {
			if(Red.size()<=Blue.size()) return;
			//swap(Red,Blue); //交换两个向量的内容,这样在使用匈牙利算法时可节省查找增广路径的时间
			Red.swap(Blue);
		}
		/*
		此方法识别输入图是不是二部图,核心思想是通过图的深度优先遍历,对每个顶点进行着色,
		如果相邻接的两个顶点颜色一致,则该图不是二部图
		@start: 选择一个开始的顶点进行深度优先遍历
		@Color: 当前被访问顶点的颜色
		*/
		void IsBipartite_Graph_DFS(int start,Color color) {  //pre是顶点start在DFS序列中的直接前驱顶点
			int j;
			visited[start]=true;    
			lnode *p=graph.array[start].link;
			/*
			 找到孤立点 
			*/
			if(!p) {
				isolateflag=true;         
     			isolate.push_back(start);  //加入孤立点集合
				return;
			}
			if(vertexcolor[start]==black) {  //此顶点没有打上颜色
				vertexcolor[start]=color;
				if(color==red) {
					Red.push_back(start);  //将此顶点加入红点集
					color=blue;  //将颜色转化
				}
				else {
					Blue.push_back(start);
					color=red;
				}
			}
			while(p) {
				j=p->sequence;
				if(!visited[j]) {
					if(flag==true) IsBipartite_Graph_DFS(j,color); //去检查此顶点的相邻顶点
				}
				else {
					if(vertexcolor[j]==vertexcolor[start]) {  //相关联的两个顶点颜色一样,则此图不是二分图
						cerr<<"不是二分图!"<<endl;
						Red.clear();
						Blue.clear();
						flag=false;
						return;
					}
				}
				p=p->next;
			}
		}
		/*
		此方法根据红点k,在蓝点集中找到增广路径,找到就增广
		@k: 红点
		*/
		bool DFS(int k) {
			vector<int>::iterator it;
			for(it=Blue.begin();it!=Blue.end();it++)  //试探每一个蓝点集的顶点
			{
				
				if(graph.connect[k][*it] && !visited[*it])  //如果此蓝点与红点相连,且该蓝点没有被访问过
				{
					visited[*it]=true;
					if(match[*it]==-1 || DFS(match[*it]))  //如果该蓝点没有与其匹配的红点,或者蓝点
													//有匹配的红点,那么从该红点查找匹配
					{
						match[*it]=k;    //找到增广路径,将其取反
						return true;
					}
				}
			}
			return false;
		}
		/*********************************************************************************/
		void DFS(vector<int>::iterator i,int k) {  //i指向当前的红点,k表示匹配数
			vector<int>::iterator it;
			int weight;
			if(i!=Red.end() && k<Red.size()) {
				for(it=Blue.begin();it!=Blue.end();it++) {
					if(graph.connect[*i][*it] && !visited[*it]) {  //匹配成功
						pair<int,int>p(*i,*it);  //构造一个匹配
						Stack.push(p);  //将此匹配入栈
						visited[*it]=true;
						DFS(i+1,k+1);  //递归从第i+1个红点去找匹配
						visited[*it]=false;  //将递归前的访问到蓝点变成未访问
						Stack.pop();
					}
				}
			}
			if(k==Red.size()) {  //所有红点都已经找到匹配
				perfectMatch=true;
				int j;
				for(j=0;j<k;j++) {
					tempStack.push(Stack.top());
					Stack.pop();
				}
				weight=0;
				for(j=0;j<k;j++) {
					pair<int,int>p=tempStack.top();
					weight+=graph.connect[p.first][p.second];
					tempStack.pop();
					Stack.push(p);
				}	
				pair<stack<pair<int,int> >,int>p(Stack,weight);
				MatchArray.push_back(p);
			}
		}
		/*
		*给定红点查找与其匹配的蓝点
		*/
		int MatchedRed(int red) {
			map<int,int>::iterator pos;
			for(pos=match.begin();pos!=match.end();pos++) {
				if(pos->second==red) return pos->first;			
			}
		}
		/*
		*给定蓝点找与其邻接的没有被访问过且不匹配的红点
		*/
		int BlueToRed(int Blue) {
			vector<int>::iterator it;
			for(it=Red.begin();it!=Red.end();it++) {
				if(graph.connect[Blue][*it] && visited[*it]==false) {
					return *it;
				}
			}
			return -1;  //找不到满足条件的红点
		}
		void setVisitedFalse() {
			int i;
			for(i=0;i<graph.vertexnum;i++) visited[i]=false;  //将所有顶点都设置为未访问
		}
		public:
			void test() {
				int blue;
				do{
					setVisitedFalse();
					cin>>blue;
					cout<<BlueToRed(blue);
				}while(blue!=-1);
			}
};

void main() {
	Bipartite_Graph<string>bg(0,0);  //不带权值的无向图
	bg.show();
	bg.MaxMatch();
	bg.MinCoveredPoints();
//	bg.Hungary();
//bg.OptimalMatch();	
}

3. 测试

原图如下：

 

在程序中输入该图

输入顶点

输入边

程序输出结果：

顶点输出

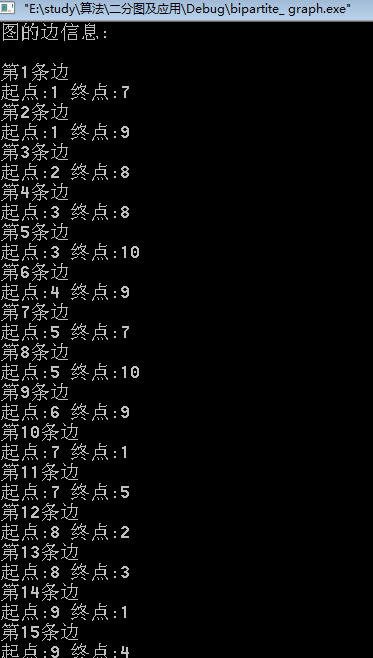
边输出

红点集，蓝点集，最大匹配，最小覆盖顶点集输出