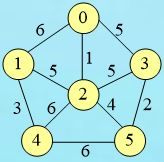
项目2 -- 最小生成树的克鲁斯卡尔算法

/*   

* Copyright (c) 2015, 烟台大学计算机与控制工程学院   

* All rights reserved.   

* 文件名称：main.cpp,graph.h,graph.cpp

* 作者：张志康  

* 完成日期：2015年11月23日   

* 版本号：vc++6.0   

*   

* 问题描述：最小生成树的克鲁斯卡尔算法

* 输入描述：

* 程序输出：

 */ 

问题及代码：   （程序中graph.h是图存储结构的“算法库”中的头文件，详情请单击链接…）

#include <stdio.h>
#include <malloc.h>
#include "graph.h"
#define MaxSize 100
typedef struct
{
    int u;     //边的起始顶点
    int v;     //边的终止顶点
    int w;     //边的权值
} Edge;

void InsertSort(Edge E[],int n) //对E[0..n-1]按递增有序进行直接插入排序
{
    int i,j;
    Edge temp;
    for (i=1; i<n; i++)
    {
        temp=E[i];
        j=i-1;              //从右向左在有序区E[0..i-1]中找E[i]的插入位置
        while (j>=0 && temp.w<E[j].w)
        {
            E[j+1]=E[j];    //将关键字大于E[i].w的记录后移
            j--;
        }
        E[j+1]=temp;        //在j+1处插入E[i]
    }
}

void Kruskal(MGraph g)
{
    int i,j,u1,v1,sn1,sn2,k;
    int vset[MAXV];
    Edge E[MaxSize];    //存放所有边
    k=0;                //E数组的下标从0开始计
    for (i=0; i<g.n; i++)   //由g产生的边集E
        for (j=0; j<g.n; j++)
            if (g.edges[i][j]!=0 && g.edges[i][j]!=INF)
            {
                E[k].u=i;
                E[k].v=j;
                E[k].w=g.edges[i][j];
                k++;
            }
    InsertSort(E,g.e);      //采用直接插入排序对E数组按权值递增排序
    for (i=0; i<g.n; i++)   //初始化辅助数组
        vset[i]=i;
    k=1;    //k表示当前构造生成树的第几条边,初值为1
    j=0;    //E中边的下标,初值为0
    while (k<g.n)       //生成的边数小于n时循环
    {
        u1=E[j].u;
        v1=E[j].v;      //取一条边的头尾顶点
        sn1=vset[u1];
        sn2=vset[v1];   //分别得到两个顶点所属的集合编号
        if (sn1!=sn2)   //两顶点属于不同的集合
        {
            printf("  (%d,%d):%d\n",u1,v1,E[j].w);
            k++;                     //生成边数增1
            for (i=0; i<g.n; i++)   //两个集合统一编号
                if (vset[i]==sn2)   //集合编号为sn2的改为sn1
                    vset[i]=sn1;
        }
        j++;               //扫描下一条边
    }
}

int main()
{
    MGraph g;
    int A[6][6]=
    {
        {0,6,1,5,INF,INF},
        {6,0,5,INF,3,INF},
        {1,5,0,5,6,4},
        {5,INF,5,0,INF,2},
        {INF,3,6,INF,0,6},
        {INF,INF,4,2,6,0}
    };
    ArrayToMat(A[0], 6, g);
    printf("最小生成树构成:\n");
    Kruskal(g);
    return 0;
}

 

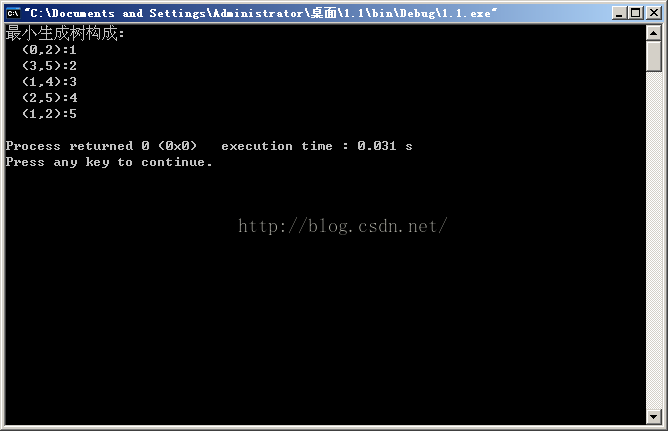
运行结果：

学习总结：