OpenGL 法线贴图 切线空间 整理

1、 What`s Bump Mapping?

Bump Mapping通过改变几何体表面各点的法线，使本来是平的东西看起来有凹凸的效果，是一种欺骗眼睛的技术：）。

我们知道，如果几何体表面有高低不平的凹凸，那么表面上各点的法线方向就会不同，那么当光照射到这些点上时，各点光照产生效果就不一样，那么我们最终看到的各点就是凹凸不平的。如果几何体表面是平的，但是各点的法线方向各不相同，当用光照模型进行光照计算后，我们看到最终渲染出来的图会是什么样呢？会看到高低不平的凹凸效果。

Bump Mapping把各象素法线相关的信息存于一张Texture中，各象素的法线就是通过从这张Texture中Sample得到的信息，进行一定的计算得到。根据Sample的方法和计算的方法不同，分为了Bump Mapping，Normal Mapping,Parallax Mapping,Parallax Occulision Mapping,Relief Mapping等等。

Bump Mapping这种思想最早是由图形学届大牛中的大牛Jim Blinn提出的，后来的Normal Mapping, Parallax Mapping,Parallax Occulision Mapping,Relief Mapping等等,均是基于同样的思想，只是考虑得越来越全面，产生的效果越来越好。

2、 Why Bump Mapping?

如果要在几何体表面表现出凹凸不平的细节，那么在建模的时候就会需要很多的三角面，如果用这样的模型去实时渲染，出来的效果是非常好，只是性能上很有可能无法忍受。Bump Mapping不需要增加额外的几何信息,就可以达到增强被渲染物体的表面细节的效果，可以大大地提高渲染速度，因此得到了广泛的应用。

3、   Bump Mapping

Jim Blinn在1978发表了一篇名为：“Simulation of Wrinkled Surfaces”，提出了Bump Mapping这个东东。Bump Mapping通过一张Height Map记录各象素点的高度信息，有了高度信息，就可以计算HeightMap中当前象素与周围象素的高度差，这个高度差就代表了各象素的坡度，用这个坡度信息去绕动法向量，得到最终法向量，用于光照计算。坡度越陡，绕动就越大。那么，根据HeighMap如何计算Normal呢？

设当前象素纹理坐标为(u,v),切线空间中切向量为T(对应纹理空间U方向)，负法线为B（对应纹理空间V方向）,Height(u,v)表示纹理坐标(u,v)处的高度值。   

du=1/HightmapWidth,dv = 1/Hightmap Height所有计算均是在切线空间，计算公式如下：

u_gradient = Height(u-du, v) - Height (u+du, v)（U方向的坡度）

v_gradient = Height(u, v-dv) - Height (u, v+dv) (V方向的坡度)

New_Normal = Normal + (T * u_gradient) + (B * v_gradient)（Normal是当前象素切线空间的Normal）。用shader片断如下：

float u_gradient = tex2D(HeightMap,texcoord+float2(-du,0) )-

                    tex2D(HeightMap,texcoord+float2(+du,0));

     float v_gradient = tex2D(HeightMap,texcoord+float2(-dv,0))-

                    tex2D(HeightMap,texcoord+float2(dv,0));

    float normal = normal + Tangent*u_gradient+Binormal*v_gradient;

 

4、 Normal Mapping

Normal Mapping也叫做Dot3 Bump Mapping,它也是Bump Mapping的一种，区别在于Normal Mapping技术直接把Normal存到一张NormalMap里面，从NormalMap里面采回来的值就是Normal，不需要像HeightMap那样再经过额外的计算。

NormalMap一般都是由HeightMap离线生成，建模工具(如Max,Maya)一般都支持导出模型的NormalMap,一般都是由高模导出NormalMap，在渲染的时候用低模＋高模导出的NormalMap，在PixelShader采样出Normal值，中运用某种光照模型，运行逐象素光照。

值得注意的是，NormalMap存的Normal是基于切线空间的，因此要进行光照计算时，需要把Normal,Light Direction,View direction统一到同一坐标空间中。一般的做法是在VS中把Light Direction和View Direction变换到Tangent Space,通过硬件Rasterrize后，在PS中便统一到切线空间，可以直接计算。Normal Map的Shader网上可以搜出一堆，这里就不贴啦。

5、Parallax Mapping

当使用Normal Mapping技术时，并没有把视线方向考滤进去。在真实世界中，如果物体表面高低不平，当视线方向不同时，看到的效果也不相同。Parallax Mapping就是为了解决此问题而提出的。

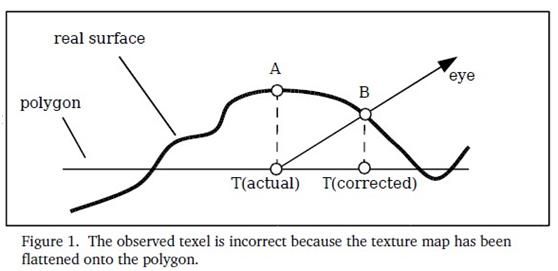
Parallax Mapping首先在一篇名为“Detailed Shape Representation with Parallax Mapping”的文章中提出。它的基本思想如下图示（本图来自Parallax Mapping with Offset Limiting: A PerPixel Approximation of Uneven Surfaces）。在图示的视线方向，如果表面是真正的凹凸不平的，如real surfacer所示，那么能看到的是B点，因此用于采样法线的正确纹理坐是TB而不是TA。

因此，我们需要对纹理坐标作偏移，为了满足实时渲染的要求，采用了取近似偏移的方法（如下图示），这种近似的算法已经可以达到比较好的效果。具体的offset计算可以参考：“Parallax Mapping with Offset Limiting: A PerPixel Approximation of Uneven Surface”，里面有详细的讲解。

 

6、Parallax Occlusion Mapping

Parallax Occlusion Mapping是对Parallax Mapping的改进，DirectX SDK中有个Sample专门讲这个，相关细节可以参看此Sample. Parallax Occlusion Mapping中实现了Self Shadow，还计算了比较精确的offset，复杂度比Parallax Mapping大，但是实现效果更好。

 

7各种Mapping的比较。

 

	高度图	法线图	随视点变化	自阴影	性能
Bump Mapping	需要	不需要	否	无	快
Normal Mapping		需要	否	无	快
Parallax Mapping	需要	需要	是	否	较快
Parallax Occlusion Mapping	需要	需要	是	是	慢

 

第一篇 tangent space--切空间


在做类似normal mapping的时候我们不可避免的要接触到tangent space--切空间；
需要在这个空间里面做光照计算；
自己经常被这些个概念混淆，试图在这篇blog里面弄清楚；
1，tangent space 与 model space
这是两个coordinate，存储normal map信息的时候是按照tangent space来存储；
model space就是一个物体所在的空间，tangent space对于3D object来说就是某一点的vertex的切平面；
而做光照计算的时候，光源是在model space，由于我们要得是夹角，所以可以把一个转换到另外一个中去；
2，转换：
tangent space象model space一样，用三个向量定义，对应x,y,z轴，名字叫tangent,normal，binormal
如果我们已知tangent，normal,binormal在model space中normalize后的值；
那么转换工作就可以通过构建3x3矩阵来实现，如果做向量变换的时候采用矩阵在右的乘法的话，
矩阵可以这样构建：|tx,nx,bx|
    |ty,ny,by|
    |tz,nz,bz|
意义也非常明显，假设vec（x,y,z)做矩阵乘法时候，那么第一项是dot(vec,float3(tx,ty,tz))
就是vec在tangent上的投影大小；
3，tangent matrix是orthogonal的
orthogonal矩阵就是它的转置是它的逆矩阵；
由于tangent,normal,binormal是正交的，而且normalize的，
所以无论推理还是验证都可以得到这个特点；


第二篇 3D中的切线空间


1、 什么是Tangent space?
Tangent space和world space，view space其实是同样的概念，均是代表三维坐标系。在这个坐标系中， X轴对应纹理坐标的U方向，沿着该轴纹理坐标U线性增大。Y轴对应纹理坐标的V方向，沿着该轴纹理坐标V线性增大。Z轴则是UXV，垂直于纹理平面。
2、 为什么需要tangent space？
在normal map等技术中，存储在texture中的值是基于tangent space的法线。因此，当我们sample这些texure中的法线进行光照计算时，必须要统一到同一坐标系下结果才正确，这时候就需要切线空间（就像是所有的local space都要统一到world space一个道理。
那么为什么normal map里面存的法线信息是基于tangent space而不是基于local sapce呢？基于local space理论上是可以的，但是这样的normal map只能用于这一个模型，不同把这个normal map用于其他模型。比如说建模了一个人，并且生成了该模型基于local space的normal map，如果我们建模同样一个人，但是放的位置和角度和之前的不一样，那么之前的normal map就不可用了，因为local space并不一样。但如果我们normal map里存的是tangent space的normal的话，就不存在这个问题，因为办要模型一样，模型上每个点的tangent space就是一样的，所谓是以不变应万变。
3、 怎样计算tangent space?
假设三角形三个坐标点为P1(u1,v1)、P2(u2,v2)、P3(u3,v3)，假设切线空间的三个基为T，B,N(T为切线方向，也就是u方向,B为负法线方向,也就是v方向),其实T和B均在三角形所在的平面上。
 P1*T =u1,P2*T=u2,P3*T=u3
 P1*B=v1,P2*B=v2,P3*B=v3
因为P1(u1,v1)、P2(u2,v2)、P3(u3,v3)均是已知的，因此可以解出T和B向量，由于N=TXB，因此便得到了该三角形的切线空间。
 
在实际编程中，可以直接调D3D的函数由Mesh来生成切线空间，但是知其然，必尽更好些。
（发现要通俗易懂地讲清楚一件事情好难，不仅要耐心，而且还要水平）
 
大家可以参考”Iterative Parallax Mapping with Slope Information”这篇文章，讲得非常清楚，但它的TBN和我求的TBN有些区别，我的是local space到切线空间的TBN,






第二篇 3D中的切线空间


1、 什么是Tangent space?
Tangent space和world space，view space其实是同样的概念，均是代表三维坐标系。在这个坐标系中， X轴对应纹理坐标的U方向，沿着该轴纹理坐标U线性增大。Y轴对应纹理坐标的V方向，沿着该轴纹理坐标V线性增大。Z轴则是UXV，垂直于纹理平面。
2、 为什么需要tangent space？
在normal map等技术中，存储在texture中的值是基于tangent space的法线。因此，当我们sample这些texure中的法线进行光照计算时，必须要统一到同一坐标系下结果才正确，这时候就需要切线空间（就像是所有的local space都要统一到world space一个道理。
那么为什么normal map里面存的法线信息是基于tangent space而不是基于local sapce呢？基于local space理论上是可以的，但是这样的normal map只能用于这一个模型，不同把这个normal map用于其他模型。比如说建模了一个人，并且生成了该模型基于local space的normal map，如果我们建模同样一个人，但是放的位置和角度和之前的不一样，那么之前的normal map就不可用了，因为local space并不一样。但如果我们normal map里存的是tangent space的normal的话，就不存在这个问题，因为办要模型一样，模型上每个点的tangent space就是一样的，所谓是以不变应万变。
3、 怎样计算tangent space?
假设三角形三个坐标点为P1(u1,v1)、P2(u2,v2)、P3(u3,v3)，假设切线空间的三个基为T，B,N(T为切线方向，也就是u方向,B为负法线方向,也就是v方向),其实T和B均在三角形所在的平面上。
 P1*T =u1,P2*T=u2,P3*T=u3
 P1*B=v1,P2*B=v2,P3*B=v3
因为P1(u1,v1)、P2(u2,v2)、P3(u3,v3)均是已知的，因此可以解出T和B向量，由于N=TXB，因此便得到了该三角形的切线空间。
 
在实际编程中，可以直接调D3D的函数由Mesh来生成切线空间，但是知其然，必尽更好些。
（发现要通俗易懂地讲清楚一件事情好难，不仅要耐心，而且还要水平）
 
大家可以参考”Iterative Parallax Mapping with Slope Information”这篇文章，讲得非常清楚，但它的TBN和我求的TBN有些区别，我的是local space到切线空间的TBN,