图象的压缩编码
在介绍图象的压缩编码之前,先考虑一个问题:为什么要压缩?其实这个问题不用我回答,你也能想得到。因为图象信息的数据量实在是太惊人了。举一个例子就明白:一张A4(210mm×297mm)幅面的照片,若用中等分辨率(300dpi)的扫描仪按真彩色扫描,其数据量为多少?让我们来计算一下:共有(300×210/25.4) ×(300×297/25.4)个象素,每个象素占3个字节,其数据量为26M字节,其数据量之大可见一斑了。
如今在Internet上,传统基于字符界面的应用逐渐被能够浏览图象信息的WWW(World Wide Web)方式所取代。WWW尽管漂亮,但是也带来了一个问题:图象信息的数据量太大了,本来就已经非常紧张的网络带宽变得更加不堪重负,使得World Wide Web变成了World Wide Wait。
总之,大数据量的图象信息会给存储器的存储容量,通信干线信道的带宽,以及计算机的处理速度增加极大的压力。单纯靠增加存储器容量,提高信道带宽以及计算机的处理速度等方法来解决这个问题是不现实的,这时就要考虑压缩。
压缩的理论基础是信息论。从信息论的角度来看,压缩就是去掉信息中的冗余,即保留不确定的信息,去掉确定的信息(可推知的),也就是用一种更接近信息本质的描述来代替原有冗余的描述。这个本质的东西就是信息量(即不确定因素)。
压缩可分为两大类:第一类压缩过程是可逆的,也就是说,从压缩后的图象能够完全恢复出原来的图象,信息没有任何丢失,称为无损压缩;第二类压缩过程是不可逆的,无法完全恢复出原图象,信息有一定的丢失,称为有损压缩。选择哪一类压缩,要折衷考虑,尽管我们希望能够无损压缩,但是通常有损压缩的压缩比(即原图象占的字节数与压缩后图象占的字节数之比,压缩比越大,说明压缩效率越高)比无损压缩的高。
图象压缩一般通过改变图象的表示方式来达到,因此压缩和编码是分不开的。图象压缩的主要应用是图象信息的传输和存储,可广泛地应用于广播电视、电视会议、计算机通讯、传真、多媒体系统、医学图象、卫星图象等领域。
压缩编码的方法有很多,主要分成以下四大类:(1)象素编码;(2)预测编码;(3)变换编码;(4)其它方法。
所谓象素编码是指,编码时对每个象素单独处理,不考虑象素之间的相关性。在象素编码中常用的几种方法有:(1)脉冲编码调制(Pulse Code Modulation,简称PCM);(2)熵编码(Entropy Coding);(3)行程编码(Run Length Coding);(4)位平面编码(Bit Plane Coding)。其中我们要介绍的是熵编码中的哈夫曼(Huffman)编码和行程编码(以读取.PCX文件为例)。
所谓预测编码是指,去除相邻象素之间的相关性和冗余性,只对新的信息进行编码。举个简单的例子,因为象素的灰度是连续的,所以在一片区域中,相邻象素之间灰度值的差别可能很小。如果我们只记录第一个象素的灰度,其它象素的灰度都用它与前一个象素灰度之差来表示,就能起到压缩的目的。如248,2,1,0,1,3,实际上这6个象素的灰度是248,250,251,251,252,255。表示250需要8个比特,而表示2只需要两个比特,这样就实现了压缩。
常用的预测编码有Δ调制(Delta Modulation,简称DM);微分预测编码(Differential Pulse Code Modulation,DPCM),具体的细节在此就不详述了。
所谓变换编码是指,将给定的图象变换到另一个数据域(如频域)上,使得大量的信息能用较少的数据来表示,从而达到压缩的目的。变换编码有很多,如(1)离散傅立叶变换(Discrete Fourier Transform,简称DFT);(2)离散余弦变换(Discrete Cosine Transform,简称DCT);(3)离散哈达玛变换(Discrete Hadamard Transform,简称DHT)。
其它的编码方法也有很多,如混合编码(Hybird Coding)、矢量量化(Vector Quantize,VQ)、LZW算法。在这里,我们只介绍LZW算法的大体思想。
值得注意的是,近些年来出现了很多新的压缩编码方法,如使用人工神经元网络(Artificial Neural Network,简称ANN)的压缩编码算法、分形(Fractl)、小波(Wavelet)、基于对象(Object Based)的压缩编码算法、基于模型(Model –Based)的压缩编码算法(应用在MPEG4及未来的视频压缩编码标准中)。这些都超出了本书的范围。
本章的最后,我们将以JPEG压缩编码标准为例,看看上面的几种编码方法在实际的压缩编码中是怎样应用的。
1哈夫曼编码
哈夫曼(Huffman)编码是一种常用的压缩编码方法,是Huffman于1952年为压缩文本文件建立的。它的基本原理是频繁使用的数据用较短的代码代替,较少使用的数据用较长的代码代替,每个数据的代码各不相同。这些代码都是二进制码,且码的长度是可变的。举个例子:假设一个文件中出现了8种符号S0,S1,S2,S3,S4,S5,S6,S7,那么每种符号要编码,至少需要3比特。假设编码成000,001,010,011,100,101,110,111(称做码字)。那么符号序列S0S1S7S0S1S6S2S2S3S4S5S0S0S1编码后变成000001111000001110010010011100101000000001,共用了42比特。我们发现S0,S1,S2这三个符号出现的频率比较大,其它符号出现的频率比较小,如果我们采用一种编码方案使得S0,S1,S2的码字短,其它符号的码字长,这样就能够减少占用的比特数。例如,我们采用这样的编码方案:S0到S7的码字分别01,11,101,0000,0001,0010,0011,100,那么上述符号序列变成011110001110011101101000000010010010111,共用了39比特,尽管有些码字如S3,S4,S5,S6变长了(由3位变成4位),但使用频繁的几个码字如S0,S1变短了,所以实现了压缩。
上述的编码是如何得到的呢?随意乱写是不行的。编码必须保证不能出现一个码字和另一个的前几位相同的情况,比如说,如果S0的码字为01,S2的码字为011,那么当序列中出现011时,你不知道是S0的码字后面跟了个1,还是完整的一个S2的码字。我们给出的编码能够保证这一点。
下面给出具体的Huffman编码算法。
(1) 首先统计出每个符号出现的频率,上例S0到S7的出现频率分别为4/14,3/14,2/14,1/14,1/14,1/14,1/14,1/14。
(2) 从左到右把上述频率按从小到大的顺序排列。
(3) 每一次选出最小的两个值,作为二叉树的两个叶子节点,将和作为它们的根节点,这两个叶子节点不再参与比较,新的根节点参与比较。
(4) 重复(3),直到最后得到和为1的根节点。
(5) 将形成的二叉树的左节点标0,右节点标1。把从最上面的根节点到最下面的叶子节点途中遇到的0,1序列串起来,就得到了各个符号的编码。
上面的例子用Huffman编码的过程如图9.1所示,其中圆圈中的数字是新节点产生的顺序。可见,我们上面给出的编码就是这么得到的。
图9.1 Huffman编码的示意图
产生Huffman编码需要对原始数据扫描两遍。第一遍扫描要精确地统计出原始数据中,每个值出现的频率,第二遍是建立Huffman树并进行编码。由于需要建立二叉树并遍历二叉树生成编码,因此数据压缩和还原速度都较慢,但简单有效,因而得到广泛的应用。
源程序就不给出了,有兴趣的读者可以自己实现。
2 行程编码
行程编码(Run Length Coding)的原理也很简单:将一行中颜色值相同的相邻象素用一个计数值和该颜色值来代替。例如aaabccccccddeee可以表示为3a1b6c2d3e。如果一幅图象是由很多块颜色相同的大面积区域组成,那么采用行程编码的压缩效率是惊人的。然而,该算法也导致了一个致命弱点,如果图象中每两个相邻点的颜色都不同,用这种算法不但不能压缩,反而数据量增加一倍。所以现在单纯采用行程编码的压缩算法用得并不多,PCX文件算是其中的一种。
3 算法的大体思想
LZW是一种比较复杂的压缩算法,其压缩效率也比较高。我们在这里只介绍一下它的基本原理:LZW把每一个第一次出现的字符串用一个数值来编码,在还原程序中再将这个数值还成原来的字符串。例如:用数值0x100代替字符串“abccddeee”,每当出现该字符串时,都用0x100代替,这样就起到了压缩的作用。至于0x100与字符串的对应关系则是在压缩过程中动态生成的,而且这种对应关系隐含在压缩数据中,随着解压缩的进行这张编码表会从压缩数据中逐步得到恢复,后面的压缩数据再根据前面数据产生的对应关系产生更多的对应关系,直到压缩文件结束为止。LZW是无损的。GIF文件采用了这种压缩算法。
要注意的是,LZW算法由Unisys公司在美国申请了专利,要使用它首先要获得该公司的认可。
4 JPEG压缩编码标准
JPEG是联合图象专家组(Joint Picture Expert Group)的英文缩写,是国际标准化组织(ISO)和CCITT联合制定的静态图象的压缩编码标准。和相同图象质量的其它常用文件格式(如GIF,TIFF,PCX)相比,JPEG是目前静态图象中压缩比最高的。我们给出具体的数据来对比一下。例图采用Windows95目录下的Clouds.bmp,原图大小为640*480,256色。用工具SEA(version1.3)将其分别转成24位色BMP、24位色JPEG、GIF(只能转成256色)压缩格式、24位色TIFF压缩格式、24位色TGA压缩格式。得到的文件大小(以字节为单位)分别为:921,654,17,707,177,152,923,044,768,136。可见JPEG比其它几种压缩比要高得多,而图象质量都差不多(JPEG处理的颜色只有真彩和灰度图)。
正是由于JPEG的高压缩比,使得它广泛地应用于多媒体和网络程序中,例如HTML语法中选用的图象格式之一就是JPEG(另一种是GIF)。这是显然的,因为网络的带宽非常宝贵,选用一种高压缩比的文件格式是十分必要的。
JPEG有几种模式,其中最常用的是基于DCT变换的顺序型模式,又称为基线系统(Baseline),以下将针对这种格式进行讨论。
4.1. JPEG的压缩原理
JPEG的压缩原理其实上面介绍的那些原理的综合,博采众家之长,这也正是JPEG有高压缩比的原因。其编码器的流程为:
图9.3 JPEG编码器流程
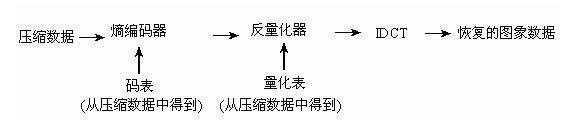
解码器基本上为上述过程的逆过程:
图9.4 解码器流程
8×8的图象经过DCT变换后,其低频分量都集中在左上角,高频分量分布在右下角(DCT变换实际上是空间域的低通滤波器)。由于该低频分量包含了图象的主要信息(如亮度),而高频与之相比,就不那么重要了,所以我们可以忽略高频分量,从而达到压缩的目的。如何将高频分量去掉,这就要用到量化,它是产生信息损失的根源。这里的量化操作,就是将某一个值除以量化表中对应的值。由于量化表左上角的值较小,右上角的值较大,这样就起到了保持低频分量,抑制高频分量的目的。JPEG使用的颜色是YUV格式。我们提到过,Y分量代表了亮度信息,UV分量代表了色差信息。相比而言,Y分量更重要一些。我们可以对Y采用细量化,对UV采用粗量化,可进一步提高压缩比。所以上面所说的量化表通常有两张,一张是针对Y的;一张是针对UV的。
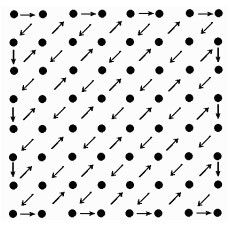
上面讲了,经过DCT变换后,低频分量集中在左上角,其中F(0,0)(即第一行第一列元素)代表了直流(DC)系数,即8×8子块的平均值,要对它单独编码。由于两个相邻的8×8子块的DC系数相差很小,所以对它们采用差分编码DPCM,可以提高压缩比,也就是说对相邻的子块DC系数的差值进行编码。8×8的其它63个元素是交流(AC)系数,采用行程编码。这里出现一个问题:这63个系数应该按照怎么样的顺序排列?为了保证低频分量先出现,高频分量后出现,以增加行程中连续“0”的个数,这63个元素采用了“之”字型(Zig-Zag)的排列方法,如图9.5所示。
图9.5 Zig-Zag
这63个AC系数行程编码的码字用两个字节表示,如图9.6所示。
图9.6 行程编码
上面,我们得到了DC码字和 AC行程码字。为了进一步提高压缩比,需要对其再进行熵编码,这里选用Huffman编码,分成两步:
(1)熵编码的中间格式表示
对于AC系数,有两个符号。符号1为行程和尺寸,即上面的(RunLength,Size)。(0,0)和(15,0)是两个比较特殊的情况。(0,0)表示块结束标志(EOB),(15,0)表示ZRL,当行程长度超过15时,用增加ZRL的个数来解决,所以最多有三个ZRL(3×16+15=63)。符号2为幅度值(Amplitude)。
对于DC系数,也有两个符号。符号1为尺寸(Size);符号2为幅度值(Amplitude)。
(2)熵编码
对于AC系数,符号1和符号2分别进行编码。零行程长度超过15个时,有一个符号(15,0),块结束时只有一个符号(0,0)。
对符号1进行Hufffman编码(亮度,色差的Huffman码表不同)。对符号2进行变长整数VLI编码。举例来说:Size=6时,Amplitude的范围是-63~-32,以及32~63,对绝对值相同,符号相反的码字之间为反码关系。所以AC系数为32的码字为100000,33的码字为100001,-32的码字为011111,-33的码字为011110。符号2的码字紧接于符号1的码字之后。
对于DC系数,Y和UV的Huffman码表也不同。
掉了这么半天的书包,你可能已经晕了,呵呵。举个例子来说明上述过程就容易明白了。
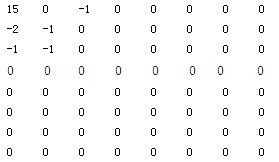
下面为8×8的亮度(Y)图象子块经过量化后的系数。
可见量化后只有左上角的几个点(低频分量)不为零,这样采用行程编码就很有效。
第一步,熵编码的中间格式表示:先看DC系数。假设前一个8×8子块DC系数的量化值为12,则本块DC系数与它的差为3,根据下表
Size Amplitude
0 0
1 –1,1
2 –3,-2,2,3
3 –7~-4,4~7
4 –15~-8,8~15
5 –31~-16,16~31
6 –63~-32,32~63
7 –127~-64,64~127
8 –255~-128,128~255
9 –511~-256,256~511
10 –1023~512,512~1023
11 –2047~-1024,1024~2047
查表得Size=2,Amplitude=3,所以DC中间格式为(2)(3)。
下面对AC系数编码。经过Zig-Zag扫描后,遇到的第一个非零系数为-2,其中遇到零的个数为1(即RunLength),根据下面这张AC系数表:
Size Amplitude
1 –1,1
2 –3,-2,2,3
3 –7~-4,4~7
4 –15~-8,8~15
5 –31~-16,16~31
6 –63~-32,32~63
7 –127~-64,64~127
8 –255~-128,128~255
9 –511~-256,256~511
10 –1023~512,512~1023
查表得Size=2。所以RunLength=1,Size=2,Amplitude=3,所以AC中间格式为(1,2)(-2)。
其余的点类似,可以求得这个8×8子块熵编码的中间格式为
(DC)(2)(3),(1,2)(-2),(0,1)(-1),(0,1)(-1),(0,1)(-1),(2,1)(-1),(EOB)(0,0)
第二步,熵编码:
对于(2)(3):2查DC亮度Huffman表得到11,3经过VLI编码为011;
对于(1,2)(-2):(1,2)查AC亮度Huffman表得到11011,-2是2的反码,为01;
对于(0,1)(-1):(0,1)查AC亮度Huffman表得到00,-1是1的反码,为0;
……
最后,这一8×8子块亮度信息压缩后的数据流为11011, 1101101, 000, 000, 000, 111000,1010。总共31比特,其压缩比是64×8/31=16.5,大约每个象素用半个比特。
可以想见,压缩比和图象质量是呈反比的,以下是压缩效率与图象质量之间的大致关系,可以根据你的需要,选择合适的压缩比。
表4.1 压缩比与图象质量的关系
| 压缩效率(单位:bits/pixel) |
图象质量 |
| 0.25~0.50 |
中~好,可满足某些应用 |
| 0.50~0.75 |
好~很好,满足多数应用 |
| 0.75~1.5 |
极好,满足大多数应用 |
| 1.5~2.0 |
与原始图象几乎一样 |
以上我们介绍了JPEG压缩的原理,其中DC系数使用了预测编码DPCM,AC系数使用了变换编码DCT,二者都使用了熵编码Huffman,可见几乎所有传统的压缩方法在这里都用到了。这几种方法的结合正是产生JPEG高压缩比的原因。顺便说一下,该标准是JPEG小组从很多种不同中方案中比较测试得到的,并非空穴来风。
上面介绍了JPEG压缩的基本原理,下面介绍一下JPEG的文件格式。
2. JPEG的文件格式
JPEG文件大体上可以分成以下两个部分:标记码(Tag)加压缩数据。先介绍标记码部分。
标记码部分给出了JPEG图象的所有信息(有点类似于BMP中的头信息,但要复杂的多),如图象的宽、高、Huffman表、量化表等等。标记码有很多,但绝大多数的JPEG文件只包含几种。标记码的结构为:
SOI
DQT
DRI
SOF0
DHT
SOS
…
EOI
标记码由两个字节组成,高字节为0XFF,每个标记码之前可以填上个数不限的填充字节0XFF。
下面介绍一些常用的标记码的结构及其含义。
(1)SOI(Start of Image)
标记结构 字节数
0XFF 1
0XD8 1
可作为JPEG格式的判据(JFIF还需要APP0的配合)
(2)APP0(Application)
标记结构 字节数 意义
0XFF 1
0XE0 1
Lp 2 APP0标记码长度,不包括前两个字节0XFF,0XE0
Identifier 5 JFIF识别码 0X4A,0X46,0X49,0X46,0X00
Version 2 JFIF版本号可为0X0101或者0X0102
Units 1 单位,等于零时表示未指定,为1表示英寸,为2表示
厘米
Xdensity 2 水平分辨率
Ydensity 2 垂直分辨率
Xthumbnail 1 水平点数
Ythumbnail 1 垂直点数
RGB0 3 RGB的值
RGB1 3 RGB的值
…
RGBn 3 RGB的值,n=Xthumbnail*Ythumbnail
APP0是JPEG保留给Application所使用的标记码,而JFIF将文件的相关信息定义在此标记中。
(3)DQT(Define Quantization Table)
标记结构 字节数 意义
0XFF 1
0XDB 1
Lq 2 DQT标记码长度,不包括前两个字节0XFF,0XDB
(Pq,Tq) 1 高四位Pq为量化表的数据精确度,Pq=0时,Q0~Qn的
值为8位,Pq=1时,Qt的值为16位,Tq表示量化表的
编号,为0~3。在基本系统中,Pq=0,Tq=0~1,也就是
说最多有两个量化表。
Q0 1或2 量化表的值,Pq=0时;为一个字节,Pq=1时,为两个
字节
Q1 1或2 量化表的值,Pq=0时;为一个字节,Pq=1时,为两个
字节
…
Qn 1或2 量化表的值,Pq=0时,为一个字节;Pq=1时,为两个
字节。n的值为0~63,表示量化表中64个值(之字形排
列)
(4)DRI(Define Restart Interval)
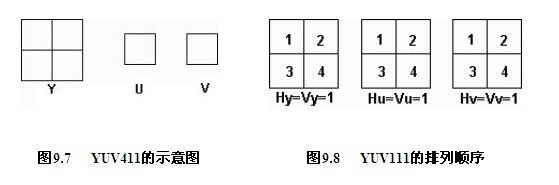
此标记需要用到最小编码单元(MCU,Minimum Coding Unit)的概念。前面提到,Y分量数据重要,UV分量的数据相对不重要,所以可以只取UV的一部分,以增加压缩比。目前支持JPEG格式的软件通常提供两种取样方式YUV411和YUV422,其含义是YUV三个分量的数据取样比例。举例来说,如果Y取四个数据单元,即水平取样因子Hy乘以垂直取样因子Vy的值为4,而U和V各取一个数据单元,即Hu×Vu=1,Hv×Vv=1。那么这种部分取样就称为YUV411。如图9.7所示:
易知YUV411有50%的压缩比(原来有12个数据单元,现在有6个数据单元),YUV422有33%的压缩比(原来有12个数据单元,现在有8个数据单元)。
那么你可能会想,YUV911,YUV1611压缩比不是更高嘛?但是要考虑到图象质量的因素。所以JPEG标准规定了最小编码单元MCU,要求Hy×Vy+Hu×Vu+Hv×Vv≤10。
MCU中块的排列方式与H,V的值有密切关系,如图9.8、图9.9、图9.10所示。
标记结构 字节数 意义
0XFF 1
0XDD 1
Lr 2 DRI标记码长度,不包括前两个字节0XFF,0XDD
Ri 2 重入间隔的MCU个数,Ri必须是一MCU行中MCU
个数的整数,最后一个零头不一定刚好是Ri个MCU。
每个重入间隔各自独立编码。
(5)SOF(Start of Frame)在基本系统中,只处理SOF0
标记结构 字节数 意义
0XFF 1
0XC0 1
Lf 2 SOF标记码长度,不包括前两个字节0XFF,0XC0
P 1 基本系统中,为0X08
Y 2 图象高度
X 2 图象宽度
Nf 1 Frame中的成分个数,一般为1或3,1代表灰度图,3
代表真彩图
C1 1 成分编号1
(H1,V1) 1 第一个水平和垂直采样因子
Tq1 1 该量化表编号
C2 1 成分编号2
(H2,V2) 1 第二个水平和垂直采样因子
Tq2 1 该量化表编号
…
Cn 1 成分编号n
(Hn,Vn) 1 第n个水平和垂直采样因子
Tqn 1 该量化表编号
(6)DHT(Define Huffman Table)
标记结构 字节数 意义
0XFF 1
0XC4 1
Lh 2 DHT标记码长度,不包括前两个字节0XFF,0XC4
(Tc,Th) 1
L1 1
L2 1
…
L16 1
V1 1
V2 1
…
Vt 1
Tc为高4位,Th为低4位。在基本系统中,Tc为0或1,为0时,指DC所用的Huffman表,为1时,指AC所用的Huffman表。Th表示Huffman表的编号,在基本系统中,其值为0或1。所以,在基本系统中,最多有4个Huffman表,如下所示:
Tc Th Huffman表编号(2×Tc+Th)
0 0
1 1
0 2
1 1 3
Ln表示每个n比特的Huffman码字的个数,n=1~16
Vt表示每个Huffman码字所对应的值,也就是我们前面所讲的符号1,对DC来说该值为(Size),对AC来说该值为(RunLength,Size)。
t=L1+L2+…L16
(7)SOS(Start of Scan)
标记结构 字节数 意义
0XFF 1
0XDA 1
Ls 2 DHT标记码长度,不包括前两个字节0XFF,0XDA
Ns 1
Cs1 1
(Td1,Ta1) 1
Cs2 1
(Td2,Ta2) 1
…
CsNs 1
(TdNs,TaNs) 1
Ss 1
Se 1
(Ah,Al) 1
Ns为Scan中成分的个数,在基本系统中,Ns=Nf(Frame中成分个数)。CSNs为在Scan中成分的编号。TdNs为高4位,TaNs为低4位,分别表示DC和AC编码表的编号。在基本系统中Ss=0,Se=63,Ah=0,Al=0。
(8)EOI(End of Image) 结束标志
标记结构 字节数 意义
0XFF 1
0XD9 1
3. JPEG基本系统解码器的实现
笔者曾经实现了一个Windows下JPEG基本系统的解码器,限于篇幅,这里就不给源程序了,只给出大体上的程序流程图(见图9.11)。
由于没有用到什么优化算法,该解码器的速度并不高,在用VC的性能评测工具Profile评测该程序时我发现最耗时的地方是反离散余弦变换(IDCT)那里,其实这是显然的,浮点数的指令条数要比整数的多得多,因此采用一种快速的IDCT算法能很大的提高性能,我这里采用是目前被认为比较好的一种快速IDCT算法,其主要思想是把二维IDCT分解成行和列两个一维IDCT。图9.12是程序运行时的画面。