【原】biginteger。大数乘法。大数运算。“无限大数字”乘法。大数乘法两种方法对比

最近在看笔试题，得知大数运算是个经常考的题目。所以有兴趣试了试。

一开始按照笔算方法自己写了个，但是时间复杂度是o(n3)。

参考了网上的算法之后，修改了自己的算法，时间复杂度变成o(n2)。

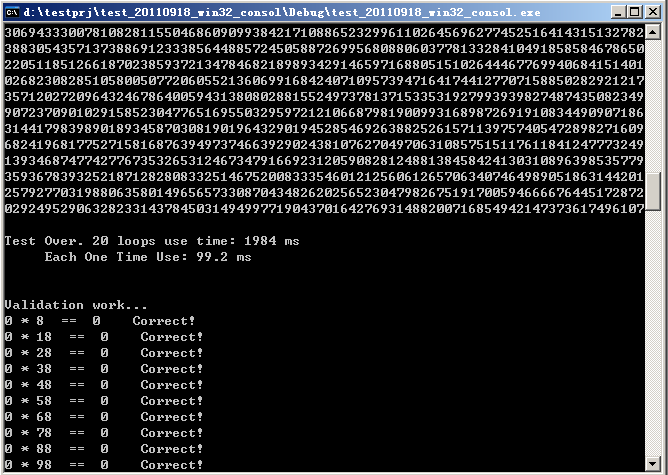
下面的测试结果中，两个2000位的数字（阿拉伯数字的位数）相乘，耗时90多毫秒。

200位，1毫秒。可以看到，复杂度的确是N的平方级别。

自己写的笨办法，每次累加之后都要判断是否有进位。但是安全。

网上有个高效的算法，使用int存储临时结果，不用每次累加后都判断一次进位。等

所有的累加都完成之后再判断，所以时间复杂度降低了一个数量级。

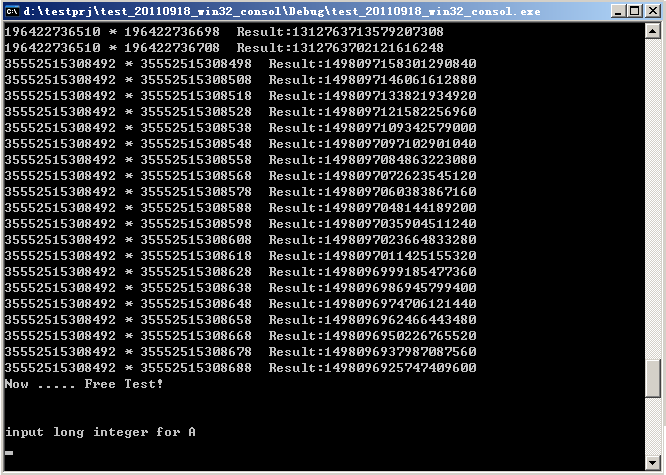
但是这样也有个坏处，就是int早晚有溢出的时候，当整数的位数足够多，

也就是达到了2的29、30、31、32次方位（当然这种情况基本没可能发生），这种方法的运算结果就是错误的了。

 

 下面是算法对应的函数。

char* BigIntMultiply ( const char * const a, const char * const b , char* const lresult)
{
	int i,j;
	int la = strlen(a);
	int lb = strlen(b);
	int rlen = la+lb;
	int* r = (int*)calloc( rlen, sizeof(int) );

	for(i = 0;i < lb; i++)
		for(j = 0; j < la; j++)
			r[rlen - 1 - i - j] += (b[lb - i - 1] - '0') * (a[la - j - 1] - '0');

	//then is there carry on current number
	for(j = rlen - 1; j >= 1; j--)
		if(r[j] > 9)
		{
			r[j-1] += r[j] / 10;
			r[j] %= 10;
		}
	//find first none_zero_index
	for(i = 0; 0 == r[i]; i++){}
		
	//mem cpy
	for(j=0; i< rlen; i++,j++)
		lresult[j] = r[i]+'0';
	lresult[j]='\0';

	free(r);
	return lresult;
}

 

 

 

下面的代码在Visual Studio 2008里面编译运行，没有问题。 Linux上没有 SYSTEMTIME，

没有atoi，itoa，GetLocalTime。所以要在Linux运行，得相应的修改一下。

#include <iostream>
#include <assert.h>
#include <stdio.h>
#include <time.h>
#include <windows.h>
#include <malloc.h>


using namespace std;

const int MAX = 2001;

char num1[MAX];
char num2[MAX];
char result[2*MAX];


void  SafeGetNumFromStr ( char* num, char* str);
char* BigIntMultiply ( const char * const a, const char * const b , char* const lresult);
void  multiply( const char *a, const char *b);

int main(int argc, char *argv[])
{
	//test speed
	cout<<"\n\nspeed test... Number of digits is : "<<MAX-1<<"\n";
	int i;
	const int TEST_TIME = 20;
	srand((unsigned)time(NULL));
	for(i = 0;i<MAX;i++)
	{
		num1[i] = 0;
		num2[i] = 0;
	}
	//create data with random
	for(i = 0; i< MAX - 1; i++)
	{
		num1[i] = rand()%10 + '0';
		num2[i] = rand()%10 + '0';
	}

	SYSTEMTIME wtm;
	GetLocalTime(&wtm);
	long long time_start = wtm.wMilliseconds + wtm.wSecond * 1000;
	cout<<num1<<endl;
	cout<<"*\n";
	cout<<num2<<endl;
	for(i = 0; i<TEST_TIME; i++)
	{
		BigIntMultiply(num1,num2,result);
	}
	GetLocalTime(&wtm);
	cout<<"Result is:\n";
	cout<<result<<endl;
	double tmv = (double)(wtm.wMilliseconds + wtm.wSecond * 1000 - time_start);
	cout<<"Test Over. "<<TEST_TIME<<" loops use time: "<<tmv<<" ms\n";
	cout<<"     Each One Time Use: "<<tmv/(double)TEST_TIME<<" ms\n\n\n";
	


	//test validation
	cout<<"Validation work...\n";
	long long  testNum1;
	long long  testNum2;
	int testI;
	for(testNum1 = 0;testNum1<1000000000000000;testNum1 = (testNum1+1)*181+1)
		for(testI= 0;testI<200; testI++)
		{
			char a[2*MAX];
			char b[2*MAX];
			testNum2 = (testNum1+testI)<0?0:testNum1+testI;
			for(i = 0;i<MAX;i++)
			{
				num1[i] = 0;
				num2[i] = 0;
			}
			itoa(testNum1,a,10);
			itoa(testNum2,b,10);
			SafeGetNumFromStr(num1,a);
			SafeGetNumFromStr(num2,b);
			BigIntMultiply(num1,num2,result);

			if(8 == testNum2%10)
				if(testNum1*testNum2 == atoi(result))
					cout<<testNum1<<" * "<<testNum2<<"  ==  "<<testNum1*testNum2<<"    Correct!\n";
				else
					cout<<testNum1<<" * "<<testNum2<<"  Result:"<<result<<"\n";
		}
	
	
	

	//free test
	cout<<"Now ..... Free Test!\n";

	while(1)
	{
		char a[2*MAX];
		char b[2*MAX];
		cout<<"\n\ninput long integer for A"<<endl;
		cin>>a;
		cout<<"input long integer for B"<<endl;
		cin>>b;

		//get data
		SafeGetNumFromStr(num1,a);
		SafeGetNumFromStr(num2,b);
		cout<<endl<<endl;
		cout<<num1;
		cout<<"  *  ";
		cout<<num2;
		cout<<endl;
		BigIntMultiply(num1,num2,result);
		cout<<"Result is:"<<endl;
		cout<<result;
	}

	system("pause");
	return 0;
}



void SafeGetNumFromStr( char* num, char* str)
{
	memset(num,0,sizeof(num[0])*MAX);
	int i;
	int index = 0;
	for(i=0;i<2*MAX && index < MAX;i++)
	{
		if(str[i] <= '9' && str[i] >='0')
			num[index++] = str[i];
		if('\0'==str[i])
			break;
	}
	assert( 0 != index );
}



char* BigIntMultiply ( const char * const a, const char * const b , char* const lresult)
{
	int i,j;
	int la = strlen(a);
	int lb = strlen(b);
	int rlen = la+lb;
	int* r = (int*)calloc( rlen, sizeof(int) );

	for(i = 0;i < lb; i++)
		for(j = 0; j < la; j++)
			r[rlen - 1 - i - j] += (b[lb - i - 1] - '0') * (a[la - j - 1] - '0');

	//then is there carry on current number
	for(j = rlen - 1; j >= 1; j--)
		if(r[j] > 9)
		{
			r[j-1] += r[j] / 10;
			r[j] %= 10;
		}
	//find first none_zero_index
	for(i = 0; 0 == r[i]; i++){}
		
	//mem cpy
	for(j=0; i< rlen; i++,j++)
		lresult[j] = r[i]+'0';
	lresult[j]='\0';

	free(r);
	return lresult;
}