算法之美——排序算法总结

原文：http://blog.csdn.net/sangni007/article/details/7995644

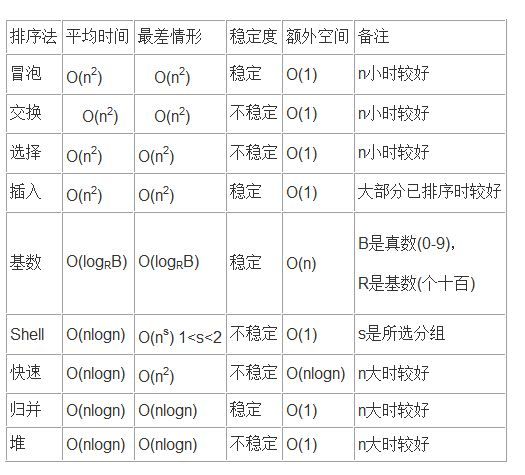
各种排序算法的简单比较

1.稳定性比较

插入排序、冒泡排序、二叉树排序、二路归并排序及其他线形排序是稳定的

选择排序（从代码看，有位置置换）、希尔排序、快速排序、堆排序是不稳定的

2.时间复杂性比较

插入排序、冒泡排序、选择排序的时间复杂性为O(n2)

其它非线形排序的时间复杂性为O(nlog2n)

线形排序的时间复杂性为O(n);

3.辅助空间的比较

线形排序、二路归并排序的辅助空间为O(n),其它排序的辅助空间为O(1);

4.其它比较

插入、冒泡排序的速度较慢，但参加排序的序列局部或整体有序时，这种排序能达到较快的速度。

反而在这种情况下，快速排序反而慢了。

当n较小时，对稳定性不作要求时宜用选择排序，对稳定性有要求时宜用插入或冒泡排序。

若待排序的记录的关键字在一个明显有限范围内时,且空间允许是用桶排序。

当n较大时，关键字元素比较随机，对稳定性没要求宜用快速排序。

当n较大时，关键字元素可能出现本身是有序的，对稳定性有要求时，空间允许的情况下。

宜用归并排序。

当n较大时，关键字元素可能出现本身是有序的，对稳定性没有要求时宜用堆排序。

*************************************************************************************

重温经典排序思想--常用排序全解  
/* 
============================================================================= 
相关知识介绍（所有定义只为帮助读者理解相关概念，并非严格定义）： 
1、稳定排序和非稳定排序 
简单地说就是所有相等的数经过某种排序方法后，仍能保持它们在排序之前的相对次序，我们就 
说这种排序方法是稳定的。反之，就是非稳定的。 
比如：一组数排序前是a1,a2,a3,a4,a5，其中a2=a4，经过某种排序后为a1,a2,a4,a3,a5， 
则我们说这种排序是稳定的，因为a2排序前在a4的前面，排序后它还是在a4的前面。假如变成a1,a4, 
a2,a3,a5就不是稳定的了。

2、内排序和外排序

在排序过程中，所有需要排序的数都在内存，并在内存中调整它们的存储顺序，称为内排序； 
在排序过程中，只有部分数被调入内存，并借助内存调整数在外存中的存放顺序排序方法称为外排序。

3、算法的时间复杂度和空间复杂度

所谓算法的时间复杂度，是指执行算法所需要的计算工作量。 
一个算法的空间复杂度，一般是指执行这个算法所需要的内存空间。

 

时间复杂度与空间复杂度详细讲解

 

**********************************************************************

//快速排序的优化

**********************************************************************

 

代码：

sort.h:

 #ifndef SORT_H
 #define SORT_H

 #include <vector>
 #include "stdlib.h"

 using namespace std;

 namespace itlab
 {
     template<typename Type> void bubbleSort(vector<Type>&, int, int);
     template<typename Type> void selectSort(vector<Type>&, int, int);
     template<typename Type> void insertSort(vector<Type>&, int, int);
     template<typename Type> void quickSort(vector<Type>&, int, int);
     template<typename Type> void mergSort(vector<Type>&, int, int);
     template<typename Type> void heapSort(vector<Type>&, int, int);

     template<typename Type> const Type& median3(vector<Type>&, int, int);
     template<typename Type> void merg(vector<Type>&, int, int, int, int);
     template<typename Type> void filterDown(vector<Type>&, int, int);

     #include "Sort_impl.h"


 }

 #endif

sort_impl.h

 /**
  * Bubble sort algorithm.
  * "a"      ---->   array of Comparable items.
  * "left"   ---->   the left-most index of the subarray.
  * "right"  ---->   the right-most index of the subarray.
  */
 template<typename Type>
 void bubbleSort( vector<Type> &a, int left, int right )
 {
     for (int i=left; i<right; i++)
     {
         //若array有序，遍历一次，则sorted=true，直接跳出函数即可;
         bool sorted = true;
         for (int j=right; j>i; j--)
         {
             if (a[j] < a[j-1])
             {
                 swap(a[j],a[j-1]);
                 sorted = false;
             }
         }
         if (sorted)
         {
             return;
         }
     }
 }

 /**
  * selection sort algorithm.
  * "a"      ---->   array of Comparable items.
  * "left"   ---->   the left-most index of the subarray.
  * "right"  ---->   the right-most index of the subarray.
  */
 template<typename Type>
 void selectSort( vector<Type> &a, int left, int right )
 {
     for (int i=left; i<right; i++)
     {
         int minPos = i;
         for (int j=i+1; j<right; j++)
         {
             if (a[j]<a[minPos])
             {
                 minPos = j;
             }
         }

         if (i!=minPos)
         {
             swap(a[i],a[minPos]);
         }
     }
 }

 /**
  * Insertion sort algorithm.
  * "a"      ---->   array of Comparable items.
  * "left"   ---->   the left-most index of the subarray.
  * "right"  ---->   the right-most index of the subarray.
  */
 template<typename Type>
 void insertSort( vector<Type> &a, int left, int right )
 {

     for (int i=left+1; i<=right; i++)//one insertion;
     {
         Type tmp = a[i];
         int j;
 //      for (j=i-1; j>=left && a[j]>tmp; j--)// insert a[i];
 //      {
 //          a[j+1] = a[j];
 //      }
 //      a[j+1]=tmp;
         for (j=i; j>left && a[j-1]>tmp; j--)
         {
             a[j] = a[j-1];
         }
         a[j] = tmp;
     }
 }

 /**
  * Internal quicksort method that makes recursive calls.
  * Uses median-of-three partitioning and a cutoff of 20.
  * "a"      ---->   array of Comparable items.
  * "left"   ---->   the left-most index of the subarray.
  * "right"  ---->   the right-most index of the subarray.
  */
 template <typename Type>
 void quickSort( vector<Type> &a, int left, int right )
 {
     if ( left+20 <= right)
     {
         Type pivot = median3(a, left, right);

         //begin partitioning
         int i = left, j = right-1;
         for(;;)
         {
             while (a[++i] < pivot){ }
             while (pivot < a[--j]){ }

             if (i < j)
                 swap(a[i], a[j]);
             else
                 break;
         }
         //Restore pivot
         swap(a[i], a[right-1]);//restore pivot;pivot的位置已经确定！下一步只对除a[i]外的两个子序列排序。i指向的肯定是第一个大于pivot的值

         //sort small elements
         quickSort(a, left, i-1);
         //sort large elements
         quickSort(a, i+1, right);

     }
     else
         insertSort(a,left,right);
 }

 /**
  * Return median of left, center, and right.
  * Order these and hide the pivot.
  */
 template <typename Type>
 const Type& median3( vector<Type> &a, int left, int right )
 {
     int center = (left + right) / 2;
     //顺序不能错;
     if (a[left] > a[center])
     {
         swap(a[left], a[center]);
     }
     if (a[left] > a[right])
     {
         swap(a[left], a[right]);
     }
     if (a[center] > a[right])
     {
         swap(a[center], a[right]);
     }

     swap( a[center], a[right-1] );///////////////////////////

     return a[right-1];

 }

 /**
  * Merg sort algorithm (nonrecursion).
  * "a"      ---->   array of Comparable items.
  * "left"   ---->   the left-most index of the subarray.
  * "right"  ---->   the right-most index of the subarray.
  */
 template <typename Type>
 void mergSort( vector<Type> &a, int left, int right )
 {
     int left1, right1, left2, right2,
         n = right - left + 1,
         size = 1;

     while( size < n )
     {
         left1 = left;

         while( left1+size < n )
         {
             left2 = left1+size;
             right1 = left2-1;
             if( left2+size > n )
                 right2 = right;
             else
                 right2 = left2+size-1;

             merg( a, left1, right1, left2, right2 );

             left1 = right2+1;
         }

         size *= 2;
     }


 }

 /**
  * Merg two subsequence to a bigger one.
  * The first subsequence is a[left1] ... a[right1], and
  * The second subsqeuence is a[left2] ... a[right2].
  */
 template <typename Type>
 void merg( vector<Type> &a, int left1, int right1, int left2, int right2 )
 {
     int k = 0,
         i = left1,
         j = left2,
         n1 = right1-left1+1,
         n2 = right2-left2+1;

     Type *tmp = new Type[n1+n2];
 //开始并排
     while( i <= right1 && j <= right2 )
         if( a[i] < a[j] )
             tmp[k++] = a[i++];
         else
             tmp[k++] = a[j++];
 //合并完成后，有个子序列还没排完
     while( i <= right1 )
         tmp[k++] = a[i++];
     while( j <= right2 )
         tmp[k++] = a[j++];
 //重新放回序列
     for( int i=0; i<n1; ++i )
         a[left1++] = tmp[i];
     for( int i=0; i<n2; ++i )
         a[left2++] = tmp[n1+i];

     delete []tmp;
 }

 /**
  * Heap sort algorthm.
  * "a"      ---->   array of Comparable items.
  * "left"   ---->   the left-most index of the subarray.
  * "right"  ---->   the right-most index of the subarray.
  */
 template <typename Type>
 void heapSort(vector<Type> &a, int left, int right)
 {
     int n = right-left+1;
     vector<Type> tmp(n);
     //assign value to tmp[]; sorting tmp[];
     for ( int i=0; i<n; i++)
     {
         tmp[i] = a[left+i];
     }
     //从第一个拥有孩子节点的位置n/2,开始排序,
     //从下向上，形成一个大根堆;
     for (int i=n/2; i>=0; i--)
     {
         filterDown(tmp, i, n);
     }
     //每循环一次,把大根与末尾元素互换;
     //然后从上到下排序一次，再次形成一个大根堆
     for (int j=n-1; j>=0; j--)
     {
         swap(tmp[0], tmp[j]);
         filterDown(tmp,0,j);
     }
     //assign sorted value to array
     for (int i=0; i<n; i++)
     {
         a[left+i] = tmp[i];
     }
 }

 /**
  * Percolate down the heap.
  * "i"  ---->  the position from which to percolate down.
  * "n"  ---->  the logical size of the binary heap.
  */
 template <typename Type>
 void filterDown( vector<Type> &a, int i, int n )//a为待排序列，i为某个排序父节点位置，n为待排序列元素个数；
 {
     int child;
     Type tmp;

     for (tmp=a[i]; 2*i+1<n; i=child)
     {
         child = 2*i+1;
         if (child!=n-1 && a[child]<a[child+1])
         {
             child++;//找出孩子节点中最大的一个
         }
         if (tmp < a[child])
         {
             //a[i] = a[child];
             swap(a[i],a[child]);//若父节点小于孩子节点，则互换
         }
         else
             break;
     }
 }

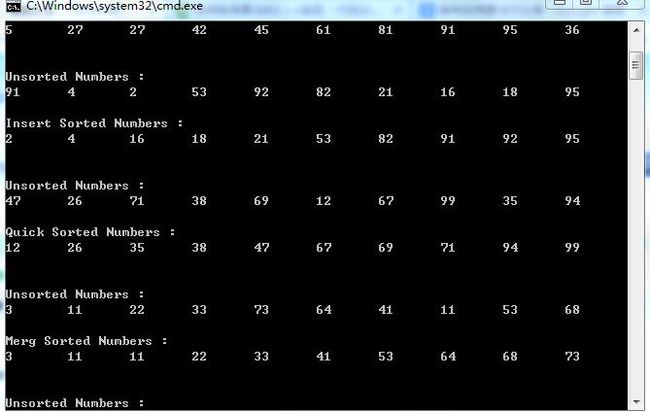
sort.cpp

其中，C/C++生成随机数。

 /*****************************************************************************
  *                                sort_test.cpp
  *
  * Sorting algorithm testing.
  *
  *
  *****************************************************************************/


 #include <iostream>
 #include<stdlib.h>
 #include "sort.h"

 #include <random>

 using namespace std;
 using namespace itlab;


 #define random(x) (rand()%x)



 const int SIZE = 10;


 template <typename Type>
 void printVector( const vector<Type> &a )
 {
     vector<int>::const_iterator itr = a.begin();
     while( itr != a.end() )
         cout << *itr++ << "\t";

     cout << endl;
 }


 int main()
 {
     vector<int> a( SIZE );

     cout << "Unsorted Numbers : " << endl;
     for( unsigned i=0; i<a.size(); ++i )
         a[i] = random(100);
     printVector( a );
     cout << "Bubble Sorted Numbers : " << endl;
     bubbleSort( a, 0, a.size()-1 );
     printVector( a );
     cout << endl;

     cout << "Unsorted Numbers : " << endl;
     for( unsigned i=0; i<a.size(); ++i )
         a[i] = random(100);
     printVector( a );
     cout << "Select Sorted Numbers : " << endl;
     selectSort( a, 0, a.size()-1 );
     printVector( a );
     cout << endl;

     cout << "Unsorted Numbers : " << endl;
     for( unsigned i=0; i<a.size(); ++i )
         a[i] = random(100);
     printVector( a );
     cout << "Insert Sorted Numbers : " << endl;
     insertSort( a, 0, a.size()-1 );
     printVector( a );
     cout << endl;

     cout << "Unsorted Numbers : " << endl;
     for( unsigned i=0; i<a.size(); ++i )
         a[i] = random(100);
     printVector( a );
     cout << "Quick Sorted Numbers : " << endl;
     quickSort( a, 0, a.size()-1 );
     printVector( a );
     cout << endl;

     cout << "Unsorted Numbers : " << endl;
     for( unsigned i=0; i<a.size(); ++i )
         a[i] = random(100);
     printVector( a );
     cout << "Merg Sorted Numbers : " << endl;
     mergSort( a, 0, a.size()-1 );
     printVector( a );
     cout << endl;

     cout << "Unsorted Numbers : " << endl;
     for( unsigned i=0; i<a.size(); ++i )
         a[i] = random(100);
     printVector( a );
     cout << "Heap Sorted Numbers : " << endl;
     heapSort( a, 0, a.size()-1 );
     printVector( a );
     cout << endl;

     return 0;
 }