每天学一点算法-DFS

DFS

深度优先算法

定义

深度优先搜索算法（Depth-First-Search），是搜索算法的一种。它沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所有边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。DFS 属于盲目搜索。

　　深度优先搜索是图论中的经典算法，利用深度优先搜索算法可以产生目标图的相应拓扑排序表，利用拓扑排序表可以方便的解决很多相关的图论问题，如最大路径问题等等。一般用堆数据结构来辅助实现 DFS 算法。

步骤

1.访问顶点v；

2.  依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问；

3.  若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

上述描述可能比较抽象，举个实例：

　　DFS 在访问图中某一起始顶点 v 后，由 v 出发，访问它的任一邻接顶点 w1；再从 w1 出发，访问与 w1 邻 接但还没有访问过的顶点 w2；然后再从 w2 出发，进行类似的访问，… 如此进行下去，直至到达所有的邻接顶点都被访问过的顶点 u 为止。

　　接着，退回一步，退到前一次刚访问过的顶点，看是否还有其它没有被访问的邻接顶点。如果有，则访问此顶点，之后再从此顶点出发，进行与前述类似的访问；如果没有，就再退回一步进行搜索。重复上述过程，直到连通图中所有顶点都被访问过为止。

使用于找出一条走出迷宫的路问题。

时间复杂度

当用二维数组表示邻接矩阵作图的存储结构时，查找每个顶点的邻接点所需时间为

O(n^2),

其中n为顶点数．

而当以邻接表作图的存储结构时，找邻接点所需时间为O(e),其中e为无向图中边的数或有向图中弧的数。

由此，当以邻接表作存储结构时，深度优先搜索遍历图的时间复杂度为

O(n+e).

代码

有向图

public class DFS {

	static Map<Integer, String> points = new HashMap<Integer, String>();

	static {
		points.put(0, "A");
		points.put(1, "B");
		points.put(2, "C");
		points.put(3, "D");
		points.put(4, "E");

	}

	public static void main(String[] args) {
		// 邻接矩阵表示图的存储结构
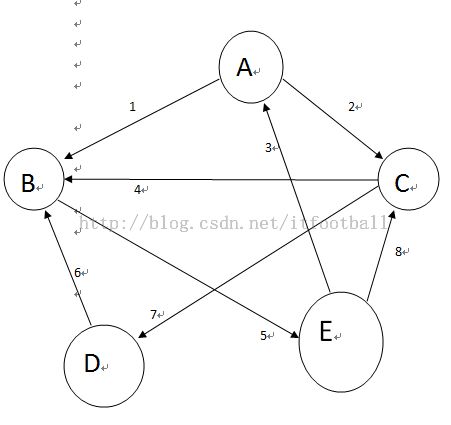
		int[][] datas = { { min, 1, 2, max, max },// A点到其他点的距离
				{ max, min, max, max, 5 },// B点到其他点的距离
				{ max, 4, min, 7, max },// C点到其他点的距离
				{ max, 6, max, min, max },// D点到其他点的距离
				{ 3, max, 8, max, min } // E点到其他点的距离
		};
		DFS dfs = new DFS();
		Scanner scanner = new Scanner(System.in);
		while (true) {
			System.out.println("请输入起始点: ");
			Integer index = scanner.nextInt();
			System.out.println(points.get(index) + "点到各条有效路径长分别为 : ");
			dfs.traverse_DFS(datas, index);
		}

	}

	// 自己与自己的距离
	static int min = 0;
	// 没有有向图的节点之间的距离
	static int max = Integer.MAX_VALUE;
	private static int[][] arcs;
	// 保存已遍历的节点,索引代表节点号,值代表是否已被所遍历
	private static boolean[] hasVisit;

	private void traverse_DFS(int[][] datas, int begin) {
		if (datas == null || datas.length == 0
				|| datas[0].length != datas.length) {
			System.out.println("邻接矩阵有问题,退出！");
			return;
		}
		arcs = datas;
		hasVisit = new boolean[datas.length];
		for (int i = 0; i < datas.length; i++) {
			hasVisit[i] = false;
		}
		recur_DFS(begin);
		{
			sum();
		}
	}

	static List<Integer> path = new ArrayList<Integer>();

	private void recur_DFS(int begin) {
		hasVisit[begin] = true;
		System.out.println("添加顶点: " + points.get(begin));
		path.add(begin);
		if (begin == 0) {
			System.out.println("start");
		}
		for (int i = 0; i < arcs.length; i++) {
			int num = arcs[begin][i];
			boolean flag = hasVisit[i];
			if (min != num && max != num && !flag) {
				recur_DFS(i);
			}
		}
	}

	private int sum() {
		System.out.println("=================start=======================");
		int sum = 0;
		for (int i = 0; i < path.size(); i++) {
			System.out.println("经过顶点 : " + points.get(path.get(i)));
			if (i > 0) {
				System.out.println("顶点" + points.get(path.get(i - 1)) + "与顶点"
						+ points.get(path.get(i)) + "的距离为 : "
						+ arcs[path.get(i - 1)][path.get(i)]);
				if (arcs[path.get(i - 1)][path.get(i)] == max
						|| arcs[path.get(i - 1)][path.get(i)] == min) {
					System.out.println("无法遍历所有顶点,该方法不可行");
					path.clear();
					return 0;
				}
				sum += arcs[path.get(i - 1)][path.get(i)];
			}
		}
		if (sum != 0)
			System.out.println("路线的权值和为 : " + sum);
		System.out.println("========================================");
		path.clear();
		return sum;
	}
}

请输入起始点: 
2
C点到各条有效路径长分别为 : 
添加顶点: C
添加顶点: B
添加顶点: E
添加顶点: A
start
添加顶点: D
=================start=======================
经过顶点 : C
经过顶点 : B
顶点C与顶点B的距离为 : 4
经过顶点 : E
顶点B与顶点E的距离为 : 5
经过顶点 : A
顶点E与顶点A的距离为 : 3
经过顶点 : D
顶点A与顶点D的距离为 : 2147483647
无法遍历所有顶点,该方法不可行
请输入起始点: 
1
B点到各条有效路径长分别为 : 
添加顶点: B
添加顶点: E
添加顶点: A
start
添加顶点: C
添加顶点: D
=================start=======================
经过顶点 : B
经过顶点 : E
顶点B与顶点E的距离为 : 5
经过顶点 : A
顶点E与顶点A的距离为 : 3
经过顶点 : C
顶点A与顶点C的距离为 : 2
经过顶点 : D
顶点C与顶点D的距离为 : 7
路线的权值和为 : 17
========================================
请输入起始点: 
0
A点到各条有效路径长分别为 : 
添加顶点: A
start
添加顶点: B
添加顶点: E
添加顶点: C
添加顶点: D
=================start=======================
经过顶点 : A
经过顶点 : B
顶点A与顶点B的距离为 : 1
经过顶点 : E
顶点B与顶点E的距离为 : 5
经过顶点 : C
顶点E与顶点C的距离为 : 8
经过顶点 : D
顶点C与顶点D的距离为 : 7
路线的权值和为 : 21
========================================
请输入起始点: 

无向无权图

public class DFS2 {
	static Map<Integer, String> points = new HashMap<Integer, String>();

	static {
		points.put(0, "A");
		points.put(1, "B");
		points.put(2, "C");
		points.put(3, "D");
		points.put(4, "E");
		points.put(5, "F");
		points.put(6, "G");
		points.put(7, "H");
		points.put(8, "I");

	}
	boolean[] hasVisits;
	int[][] arcs;

	public void search(int[][] args) throws InterruptedException {
		if (args == null || args.length == 0 || args.length != args[0].length) {
			System.out.println("邻接矩阵有问题,退出");
			return;
		}
		arcs = args;
		hasVisits = new boolean[args.length];
		for (int j = 0; j < args.length; j++) {
			hasVisits[j] = false;
		}
		for (int i = 0; i < args.length; i++) {
			System.out.println("============ " + points.get(i));
			if (!hasVisits[i])
				recur_DFS(i);
		}
	}

	private void recur_DFS(int begin) {
		hasVisits[begin] = true;
		System.out.println("经过顶点 : " + points.get(begin));
		for (int i = 0; i < arcs.length; i++) {
			if (arcs[begin][i] == 1 && !hasVisits[i])
				recur_DFS(i);
		}
	}

	public static void main(String[] args) {
		DFS2 dfs2 = new DFS2();
		// 无向图,无权值,用邻接矩阵表示如下
		int[][] datas = { { 0, 1, 0, 0, 0, 1, 0, 0, 0 },// A点矩阵
				{ 1, 0, 1, 0, 0, 0, 1, 0, 1 },// B点矩阵
				{ 0, 1, 0, 1, 0, 0, 0, 0, 1 },// C点矩阵
				{ 0, 0, 1, 0, 1, 0, 1, 1, 1 },// D点矩阵
				{ 0, 0, 0, 1, 0, 1, 0, 1, 0 },// E点矩阵
				{ 1, 0, 0, 0, 1, 0, 1, 0, 0 },// F点矩阵
				{ 0, 1, 0, 1, 0, 1, 0, 1, 0 },// G点矩阵
				{ 0, 0, 0, 1, 1, 0, 1, 0, 0 },// H点矩阵
				{ 0, 1, 1, 1, 0, 0, 0, 0, 0 },// I点矩阵
		};
		try {
			dfs2.search(datas);
		} catch (InterruptedException e) {
			e.printStackTrace();
		}
	}

}

输出

============ A
经过顶点 : A
经过顶点 : B
经过顶点 : C
经过顶点 : D
经过顶点 : E
经过顶点 : F
经过顶点 : G
经过顶点 : H
经过顶点 : I
============ B
经过顶点 : B
经过顶点 : A
经过顶点 : F
经过顶点 : E
经过顶点 : D
经过顶点 : C
经过顶点 : I
经过顶点 : G
经过顶点 : H
============ C
经过顶点 : C
经过顶点 : B
经过顶点 : A
经过顶点 : F
经过顶点 : E
经过顶点 : D
经过顶点 : G
经过顶点 : H
经过顶点 : I
============ D
经过顶点 : D
经过顶点 : C
经过顶点 : B
经过顶点 : A
经过顶点 : F
经过顶点 : E
经过顶点 : H
经过顶点 : G
经过顶点 : I
============ E
经过顶点 : E
经过顶点 : D
经过顶点 : C
经过顶点 : B
经过顶点 : A
经过顶点 : F
经过顶点 : G
经过顶点 : H
经过顶点 : I
============ F
经过顶点 : F
经过顶点 : A
经过顶点 : B
经过顶点 : C
经过顶点 : D
经过顶点 : E
经过顶点 : H
经过顶点 : G
经过顶点 : I
============ G
经过顶点 : G
经过顶点 : B
经过顶点 : A
经过顶点 : F
经过顶点 : E
经过顶点 : D
经过顶点 : C
经过顶点 : I
经过顶点 : H
============ H
经过顶点 : H
经过顶点 : D
经过顶点 : C
经过顶点 : B
经过顶点 : A
经过顶点 : F
经过顶点 : E
经过顶点 : G
经过顶点 : I
============ I
经过顶点 : I
经过顶点 : B
经过顶点 : A
经过顶点 : F
经过顶点 : E
经过顶点 : D
经过顶点 : C
经过顶点 : G
经过顶点 : H