压缩感知的常见稀疏基名称及离散傅里叶变换基
题目:压缩感知的常见稀疏基名称及离散傅里叶变换基
一、首先看九篇文献中有关稀疏基的描述:
[1]喻玲娟,谢晓春.压缩感知介绍[J]. 电视技术,2008,32(12):16-18.
常用的稀疏基有:正(余)弦基、小波基、chirplet基以及curvelet基等
[2]李树涛,魏丹.压缩传感综述[J]. 自动化学报,2009,35(11):1369-1377.
信号的稀疏表示就是将信号投影到正交变换基时,绝大部分变换系数的绝对值很小,所得到的变换向量是稀疏或者近似稀疏的,可以将其看作原始信号的一种简洁表达,这是压缩传感的先验条件,即信号必须在某种变换下可以稀疏表示,通常变换基可以根据信号本身的特点灵活选取,常用的有离散余弦变换基、快速傅里叶变换基、离散小波变换基、Curvelet基、Gabor基以及冗余字典等。
[3]杨海蓉,张成,丁大为,韦穗. 压缩传感理论与重构算法[J]. 电子学报,2011,39(1):142-148.
CS理论的三个组成要素是信号的稀疏变换(目前的稀疏变换有离散余弦变换(DCT)、小波(wavelet)、curvelet、过完备原子分解(overcomplete atomdecomposition)等)
[4]王强,李佳,沈毅.压缩感知中确定性测量矩阵构造算法综述[J]. 电子学报,2013,41(10):2041-2050.
压缩感知理论所研究的对象是可稀疏表示或可压缩的信号,常用的正交基有DCT基、FFT基、DWT基等
[5]张颖超,茅丹,胡凯.压缩传感理论在心电图信号恢复问题上的研究[J]. 计算机研究发展,2014,51(5):1018-1027.
紧支集正交小波(DbN)、近似对称的紧支集双正交小波(SymN)、Coifmant小波(CoifN)、双正交样条小波(BiorN)、快速傅里叶变换(FFT)
[6]焦李成,杨淑媛,刘芳,侯彪. 压缩感知回顾与展望[J]. 电子学报,2011,39(7):1651-1662.
从不同的角度,我们可以将字典进行不同的分类。例如按照字典中原子是否正交可以分为正交基字典和过完备冗余字典,按照字典中原子的来源又可以分为正交变换字典、框架字典和统计学习获得的字典等。本节将讨论如下几种情况下的稀疏表示:正交基字典(标准正交基字典一般由一个正交变换得到,如Fourier变换、DCT变换、沃尔什变换、小波变换等)、正交级联字典、框架字典、字典学习。
[7]石光明,刘丹华,高大化,刘哲,林杰,王良君. 压缩感知理论及其研究进展[J]. 电子学报,2009,37(5):1070-1081.
从傅里叶变换到小波变换再到后来兴起的多尺度几何分析(Ridgelet, Curvelet,Bandelet, Contourlet)
文献[8]指出光滑信号的Fourier系数、小波系数、有界变差函数的全变差范数、振荡信号的Gabor系数及具有不连续边缘的图像信号的Curvelet系数等都具有足够的稀疏性。
从冗余字典的构成角度业讲,文献[16]中提出使用局部Cosine基来刻画声音信号的局部频域特性;利用bandlet基来刻画图像中的几何边缘,还可以把其它的具有不同形状的基函数归入字典,如适合刻画纹理的Gabor基、适合刻画轮廓的Curvelet基等等。
[8]戴琼海,付长军,季向阳.压缩感知研究[J].计算机学报,2011,34(3):425-434.
Harr小波基、DaubechiesD4&D8小波
[9]李坤,马彩文,李艳,陈萍.压缩感知重构算法综述[J]. 红外与激光工程,2013,42(z1):225-232.
变换基可以为某种已被广泛应用的基,如小波基、傅里叶基、局部傅里叶基等,基中关于正交基的选择可以参考文献[1][7].另外可以使用紧框架(原子字典)来对信号进行稀疏表示,如曲线波Curvelets和轮廓波Contourlets,这两类变换基具有更好的方向性,并且各向异性,少量系数即可有效地捕捉图像的边缘轮廓,在边缘表示方面优于小波。
二、把以上九篇文献中提到的稀疏基归纳分类一下:
1、正(余)弦基、离散余弦变换基、离散余弦变换(DCT)、DCT基、DCT变换
2、小波基、离散小波变换基、小波(wavelet)、紧支集正交小波(DbN)、近似对称的紧支集双正交小波(SymN)、Coifmant小波(CoifN)、双正交样条小波(BiorN)、小波变换、小波系数、Harr小波基、DaubechiesD4&D8小波、小波基
3、chirplet基
4、curvelet基、Curvelet基、curvelet、Curvelet系数、曲线波Curvelets
5、快速傅里叶变换基、FFT基、快速傅里叶变换(FFT)、Fourier变换、Fourier系数、傅里叶基、局部傅里叶基
6、Gabor基、Gabor系数
7、DWT基
8、沃尔什变换
9、bandlet基
10、Contourlet、轮廓波Contourlets
11、其它:全变差范数、冗余字典、过完备原子分解、正交级联字典、框架字典、字典学习
注:上面分类中,第一类除第1个外其它都指的DCT;第二类应该大类是小波基,只是小波基分了不同的种类;第三类至第十类应该各自指的都是一个内容,第十一类感觉比较抽象不好说明白就不说了。其中第五类局部傅里叶基还不清楚和傅里叶基有什么区别(看名字应该是傅里叶基的部分列向量组成的???待考证!)。
三、什么是稀疏基
这里仅说正交变换基吧,稀疏基其实就是指的某种正交变换的变换矩阵列向量组成的基。下面说离散傅里叶变换基,也就是第五类,这样更容易说清楚。
四、离散傅里叶变换基
离散傅里叶变换(Discrete Fourier Transform, DFT)的正变换公式如下:

可将变换写为矩阵形式:

即 X=WNx
变换矩阵:
这里的变换矩阵WN的列向量不是单位向量,因此变换矩阵WN不是正交矩阵(正交阵是自身与自身的转置相乘等于单位阵),将变换矩阵WN除以一个系数使其变为正交矩阵可得离散傅里叶变换基(矩阵):
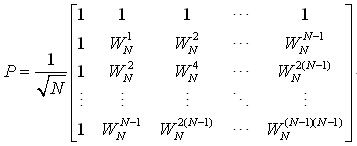
这个矩阵各列向是是单位向量且两两正交,因此称为规范正交基或标准正交基。
正交变换是有优点的,如同济线性代数第五版第116页:

维基百科的词条离散傅里叶变换矩阵中也有提及:
其实就是保持变换前后的能量一致。
五、如何得到离散傅里叶变换基
在Matlab中可以通过函数dftmtx(N)来得到,这个命令得到的是变换矩阵WN,再对其除上一个根号N即可:dftmtx(N)/sqrt(N)
如果打开dftmtx的Matlab的源文件就可以知道这个函数就包括一条指令:D = fft(eye(n));
因此也可以直接用这条命令来得到离散傅里叶变换基:fft(eye(N))/sqrt(N)
例如,沙威的压缩感知开源代码中就是用fft(eye(N))/sqrt(N)得到的离散傅里叶变换基(代码注释中注为傅里叶正变换矩阵),可参见本人的博文或Rachel Zhang的博文。