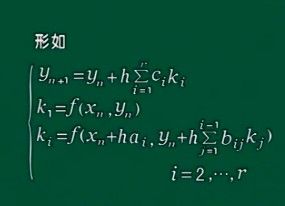龙格库塔C 语言编程实现

最新一直在学一门很苦逼的课程《数值分析》，哎，高等数学没学好现在后悔了呀，哎回来再恶补，现在说正事。

龙格库塔很牛掰的名字，是两个国外数学家的名字的合并，应该又是两个大牛。

这个方法主要是用来解决微分方程的解，大体思路就是用差分代替微分。细节我就不说了，大家可以去百度，我这里直接给出龙格库塔家族的通式：

这个是龙格库塔家族的通式，如果我们取累加和中的r为4则可以得到如下公式：

这就是四阶龙格库塔方程，据说这里的精度很好，可以精确到小数点后6位。

方程组中的h为差分的步长。

下面给出c语言实现的代码：

#include<stdlib.h> 
#include<stdio.h> 
/*n表示几等分，n+1表示他输出的个数*/ 
int RungeKutta(double y0,double a,double b,int n,double *x,double *y,int style,double (*function)(double,double)) 
{ 
	double h=(b-a)/n,k1,k2,k3,k4; 
	int i; 
	x[0]=a; 
	y[0]=y0; 
	switch(style) 
	{ 
	case 2: 
		for(i=0;i<n;i++) 
		{ 
			x[i+1]=x[i]+h; 
			k1=function(x[i],y[i]); 
			k2=function(x[i]+h/2,y[i]+h*k1/2); 
			y[i+1]=y[i]+h*k2; 
		} 
		break; 
	case 3: 
		for(i=0;i<n;i++) 
		{ 
			x[i+1]=x[i]+h; 
			k1=function(x[i],y[i]); 
			k2=function(x[i]+h/2,y[i]+h*k1/2); 
			k3=function(x[i]+h,y[i]-h*k1+2*h*k2); 
			y[i+1]=y[i]+h*(k1+4*k2+k3)/6; 
		} 
		break; 
	case 4: 
		for(i=0;i<n;i++) 
		{ 
			x[i+1]=x[i]+h; 
			k1=function(x[i],y[i]); 
			k2=function(x[i]+h/2,y[i]+h*k1/2); 
			k3=function(x[i]+h/2,y[i]+h*k2/2); 
			k4=function(x[i]+h,y[i]+h*k3); 
			y[i+1]=y[i]+h*(k1+2*k2+2*k3+k4)/6; 
		} 
		break; 
	default: 
		return 0; 
	} 
	return 1; 
} 
double function(double x,double y) 
{ 
	return y-2*x/y; 
} 
//例子求y'=y-2*x/y(0<x<1);y0=1; 

int main() 
{ 
	double x[6],y[6]; 
	printf("用二阶龙格-库塔方法\n"); 
	RungeKutta(1,0,1,5,x,y,2,function); 
	for(int i=0;i<6;i++) 
		printf("x[%d]=%f,y[%d]=%f\n",i,x[i],i,y[i]); 
	printf("用三阶龙格-库塔方法\n"); 
	RungeKutta(1,0,1,5,x,y,3,function); 
	for(i=0;i<6;i++) 
		printf("x[%d]=%f,y[%d]=%f\n",i,x[i],i,y[i]); 
	printf("用四阶龙格-库塔方法\n"); 
	RungeKutta(1,0,1,5,x,y,4,function); 
	for(i=0;i<6;i++) 
		printf("x[%d]=%f,y[%d]=%f\n",i,x[i],i,y[i]); 
	return 1;
}

结果为：