迪杰斯特拉算法

       迪杰斯特拉算法不懂？看严蔚敏的书还是看不懂？就看这篇文章吧，博主我一大优点就是表述能力比较强。也就是说，要么我自己不懂，我懂了以后一定能让别人弄懂。

1，迪杰斯特拉算法介绍（转载自：http://gelivable.blog.51cto.com/2250777/427009）

迪杰斯特拉算法是典型最短路径算法，用于计算图或网中某个特定顶点到其他所有顶点的最短路径。主要特点是以起始点为中心向外，层层扩展，直到扩展覆盖所有顶点。

2，迪杰斯特拉算法思想

设G=(V,E)为一个带全有向图，把图中顶点集合V分成两组。第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将所到达最短路径的顶点加入到集合S中，直到全部顶点都加入到S中）。第二组为其余未确定最短路径的顶点集合（用U表示，U=V-S，U中的顶点不断的加入到S中，直到U为空，S=V）。在U加入S的过程中，始终保持源点到S中各顶点的最短路径长度小于或等于源点到U中任意顶点的最短路径长度。

3，迪杰斯特拉算法执行步骤

设 n 为图 G=(V,E) 中的顶点数，dist[n] 存放从源点到每个终点当前最短路径的长度，path[n] 存放相应路径，S 为已求得最短路径的终点的集合，U为V-S,初始为不含有源点的所有顶点。

（1）初始化已求的最短路径的集合S为只含有元素源点a，S=｛a｝。

（2）从U中选取一个距离源点v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

（3）以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u（u U）的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值为顶点k的距离加上顶点k到u边上的权。

（4）重复步骤（2）和（3）直到所有顶点都包含在S中。

4，迪杰斯特拉算法举例说明

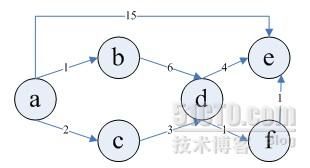
（1）有向图如下，以a为源点，求源点a到其他各顶点的最短路径。

（2）算法详细步骤如下表：

步骤	S集合中	U集合中
初始化	选入a，此时s={a} 此时最短路径有a->a=0 以a为中间点，从a开始找	U={b,c,d,e,f} a->b=1 a->c=2 a->e=15 a->其他U中顶点为无穷
1	从U={b,c,d,e,f}中发现路径a->b=1最短 选入b，S={a,b} 此时最短路径有a->a=0,a->b=1 以b为中间点，从a->b=1这条最短路径开始找	U={c,d,e,f} (a->b->d=7)<初始的无穷 改写a->b->d=无穷为当前的a->b->d=7 a-> b->其他U中顶点为无穷
2	从U={c,d,e,f}中发现路径a->c=2最短 选入c，S={a,b,c} 此时最短路径有 a->a=0,a->b=1,a->c=2 以b为中间点，从a->c=2这条最短路径开始找	U={d,e,f} (a->c->d=5)<已有的7 改写为a->c->d=5
3	从U={d,e,f}中发现路径a->c->d=5最短 选入d，S={a,b,c,d} 此时最短路径有 a->a=0,a->b=1,a->c=2,a->c->d=5 以d为中间点，从a->c->d=5这条最短路径开始找	U={e,f} (a->c->d->e=9)<步骤1中的15 改写为a->c->d->e=9 (a->c->d->f=6)<初始的无穷 改写为a->c->d->f=6
4	从U={e,f}中发现路径a->c->d->f=6最短 选入f，S={a,b,c,d,f} 此时最短路径有 a->a=0,a->b=1,a->c=2,a->c->d=5 a->c->d->f=6 以f为中间点，从a->c->d->f=6这条最短路径开始找	U={e} (a->c->d->f->e=7)<步骤3中改写成的9 改写为a->c->d->f->e=7
5	从U={f}中发现路径a->c->d->f->e=7最短 选入f，S={a,b,c,d,f,e} 此时最短路径有 a->a=0,a->b=1,a->c=2,a->c->d=5 a->c->d->f=6,a->c->d->f->e=7	U集合已空，查找完毕。

参考文献：

[1], http://2728green-rock.blog.163.com/blog/static/43636790200901211848284/

[2],严蔚敏，数据结构（电子版），清华大学出版社。

算法如下：（下载自百度文库，略微修改）

/*迪杰斯特拉算法算法步骤：

（1）初始时， S只包含源点。

（2）从U中选取一个距离v最小的顶点k加入S中（该选定的距离就是v到k的最短路径长度）。

（3）以k为新考虑的中间点， 修改U中各顶点的距离；若从源点v到顶点u（u U）的距离（经过顶点k）比原来距离（不经过顶点k）短， 则修改顶点u的距离值， 修改后的距离值的顶点k的距离加上边上的权。

（4）重复步骤（2）和（3）直到所有顶点都包含在S中。

*/
#include<iostream>
#include<string.h>
#include<stdlib.h>
using namespace std; 
#define M 999


int cost[ 6 ][ 6 ] = {
	{M,  M, 10, M, 30, 100}, 
	{M, M, M,  M,  M, M  }, 
	{M, 5, M,  50, M, M  }, 
	{M, M, M,  M,  M, 10 }, 
	{M, M, M,  20, M, 60 }, 
	{M, M, M,  M,  M, M  }
}; 

//edge，严蔚敏书上所说的向量D
typedef struct edge{
	int adjvex; 		//边的一个顶点
	int cost;       //权值（从起点到当前顶点的权值）
}edge; 

void main(){
	int total = 0;   //计数变量， 计算共选择节点多少个
	int adjvex[ 6 ]; //保存依次被选中的节点
	int i = 0; 
	edge lowpathcost[ 6 ]; //初始值为矩阵的第一行。
	char path[ 6 ][ 10 ] = {"0", "", "", "", "", ""}; //以0为初始节点开始计算最短路径 (路径)

	for(i = 1; i < 6; i++)
	{
		lowpathcost[ i ].cost = cost[ 0 ][ i ]; //初始化为M， 最短路径长度为矩阵的第一行权值
		if(cost[ 0 ][ i ] != M)
		{
			lowpathcost[ i ].adjvex = 0; //有数据则adjvex置为0
			//cout<<"初始存在路径的是"<<0<<"----"<<i<<endl; 
		}
	}
	int min; //保存最小权值
	int minvex; //保存最小权值边的另一顶点
	int selected[ 6 ] = {0}; //次变量是作为控制已输出的节点不再参与的判断参数

	//cout<<endl<<"开始选择顶点："<<endl; 

	for(int num = 1; num <= 5; num++)  //要选择的次数, 共6个顶点, 除掉起点
	{
		min = M; 
		for(i = 1; i <= 5; i++)
			if(min > lowpathcost[ i ].cost && !selected[ i ])
			{
				min = lowpathcost[ i ].cost; //第一次查找为10 即第一行中最小的值
				minvex = i; //此时i=2

			}
			adjvex[ ++total ] = minvex; //此时adjvex[1]为2， 存放依次选出的顶点
			//adjvex[2]=1
			if(min != M)
			{
				cout << "第 " << num << " 次被选择的顶点是:" << minvex << " .  " <<"对应的边上的权值是 " << min << endl; 
			}

			selected[ minvex ] = 1;     //已参与的节点就置为1
			for(i = 0; i < 6; i++)//这一个循环是算法步骤的第三步， D[j] + arcs[j][k] < D[k]
				if( !selected[ i ] && lowpathcost[ i ].cost > min + cost[ minvex ][ i ]  && min + cost[ minvex ][ i ] < M )//3项都要满足
				{
					lowpathcost[ i ].cost = min + cost[ minvex ][ i ]; 
					lowpathcost[ i ].adjvex = minvex; 
				}	
	}
	for(i = 1; i <= 5; i++)
		cout<<"  "<<lowpathcost[i].adjvex; 

	int eadjvex, sadjvex;   //当前顶点， 当前顶点的前驱顶点
	char ep[ 2 ]; //将当前顶点变为字符串
	for(i = 1; i <= total; i++)
	{
		eadjvex = adjvex[ i ]; 
		sadjvex = lowpathcost[ eadjvex ].adjvex; 
		ep[ 0 ] = '0' + eadjvex;
		ep[ 1 ] = '\0'; 
		char tmp[ 10 ]; 
		strcpy(tmp, path[ sadjvex ]); 
		strcpy(path[ eadjvex ], strcat(tmp, ep)); //    path[e]=sp+ep; 
		cout << "0 到顶点 " << eadjvex << " 的最短路径经历的节点依次是：" << path[ eadjvex ] << "  长度是：" << lowpathcost[ eadjvex ].cost << endl; 
	}
}