矩阵求导——Numerator Layout & Denominator Layout
突然想起这个问题了,刚刚看到有人在问某个的公式,自己闷头想了想居然都忘的差不多了,于是乎稍微整理一下供以后参考。
其实,关于矩阵求导讲的最详细的还是wiki上的页面面http://en.wikipedia.org/wiki/Matrix_calculus#Layout_conventions
关于矩阵求导,很多地方会有不同的表现形式,说到底是这么一回事,一个m维的向量 y 对n维的向量 x 求导 ∂y∂x ,得到的结果应该是m乘n还是n乘以m。具体内容可以看wikipedia。
y 的元素以列的形式布局, x 以行的形式,或是反过来,这就导致了不同的可能性:
分子布局(numerator layout):根据 y 或者 xT 来布局,也叫Jacobian formulation
分母布局(denominator layout):根据 yT 或者 x 来布局,也叫Hessian formulation
A third possibility sometimes seen is to insist on writing the derivative as ∂y∂x′ , (i.e. the derivative is taken with respect to the transpose of x) and follow the numerator layout. This makes it possible to claim that the matrix is laid out according to both numerator and denominator. In practice this produces results the same as the numerator layout.
When handling the [[gradient]] ∂y∂x and the opposite case ∂y∂x, we have the same issues. To be consistent, we should do one of the following:
If we choose numerator layout for ∂y∂x, we should lay out the [[gradient]] ∂y∂x as a row vector, and ∂y∂x as a column vector.
If we choose denominator layout for ∂y∂x, we should lay out the [[gradient]] ∂y∂x as a column vector, and ∂y∂x as a row vector.
In the third possibility above, we write ∂y∂x′ and ∂y∂x, and use numerator layout.
Not all math textbooks and papers are consistent in this respect throughout the entire paper. That is, sometimes different conventions are used in different contexts within the same paper. For example, some choose denominator layout for gradients (laying them out as column vectors), but numerator layout for the vector-by-vector derivative ∂y∂x.
Similarly, when it comes to scalar-by-matrix derivatives ∂y∂X and matrix-by-scalar derivatives ∂Y∂x, then consistent numerator layout lays out according to ” Y ”’ and ‘ XT ”, while consistent denominator layout lays out according to ” YT ”and ”X”. In practice, however, following a denominator layout for ∂Y∂x, and laying the result out according to ” YT ”, is rarely seen because it makes for ugly formulas that do not correspond to the scalar formulas. As a result, the following layouts can often be found:
”Consistent numerator layout”, which lays out ∂Y∂x according to ” Y′ ’ and ∂y∂X according to ” XT ”.
”Mixed layout”, which lays out ∂Y∂x according to ” Y ” and ∂y∂X according to ”’X”’.
Use the notation ∂y∂XT, with results the same as consistent numerator layout.
In the following formulas, we handle the five possible combinations ∂y∂x,∂y∂x,∂y∂x,∂y∂X and ∂Y∂x separately. We also handle cases of scalar-by-scalar derivatives that involve an intermediate vector or matrix. (This can arise, for example, if a multi-dimensional [[parametric curve]] is defined in terms of a scalar variable, and then a derivative of a scalar function of the curve is taken with respect to the scalar that parameterizes the curve.) For each of the various combinations, we give numerator-layout and denominator-layout results, except in the cases above where denominator layout rarely occurs. In cases involving matrices where it makes sense, we give numerator-layout and mixed-layout results. As noted above, cases where vector and matrix denominators are written in transpose notation are equivalent to numerator layout with the denominators written without the transpose.
Keep in mind that various authors use different combinations of numerator and denominator layouts for different types of derivatives, and there is no guarantee that an author will consistently use either numerator or denominator layout for all types. Match up the formulas below with those quoted in the source to determine the layout used for that particular type of derivative, but be careful not to assume that derivatives of other types necessarily follow the same kind of layout.
When taking derivatives with an aggregate (vector or matrix) denominator in order to find a maximum or minimum of the aggregate, it should be kept in mind that using numerator layout will produce results that are transposed with respect to the aggregate. For example, in attempting to find the [[maximum likelihood]] estimate of a [[multivariate normal distribution]] using matrix calculus, if the domain is a ”k”x1 column vector, then the result using the numerator layout will be in the form of a 1x”k” row vector. Thus, either the results should be transposed at the end or the denominator layout (or mixed layout) should be used.
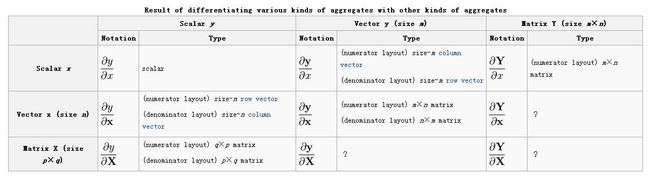
The results of operations will be transposed when switching between numerator-layout and denominator-layout notation.
=== Numerator-layout notation ===
Using numerator-layout notation, we have:Minka, Thomas P. “Old and New Matrix Algebra Useful for Statistics.” December 28, 2000. [http://research.microsoft.com/en-us/um/people/minka/papers/matrix/]
:
The following definitions are only provided in numerator-layout notation:
===Denominator-layout notation===
Using denominator-layout notation, we have:[http://www.colorado.edu/engineering/CAS/courses.d/IFEM.d/IFEM.AppD.pdf]