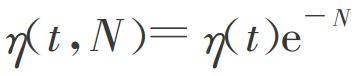自组织特征映射神经网络（SOFM）

        1981年芬兰 Helsink 大学的 T·Kohonen 教授提出一种自组织特征映射网 （Self-Organizing Feature Map ， SOFM ）， 又称 Kohonen 网 。 Kohonen 认为 ，一个神经网络接受外界输入模式时， 将会分为不同的对应区域， 各区域对输入模式具有不同的响应特征，而且这个过程是自动完成的。 自组织特征映射正是根据这一看法提出来的 ，其特点与人脑的自组织特性相类似。

一、SOFM网生物学基础

        生物学研究表明，在人脑感觉通道上，神经元的组织原理是有序排列的，输入模式接近，对应的兴奋神经元也相近。大脑皮层中神经元这种相应特点不是先天形成的，而是后天的学习自组织形成的。

         对于某一图形或某一频率的特定兴奋过程是自组织特征映射网中竞争机制的生物学基础。神经元的有序排列以及对外界信息的连续映像在自组织特征映射网中也有反映，当外界输入不同的样本时，网络中哪个位置的神经元兴奋在训练开始时时随机的。但自组织训练后会在竞争层形成神经元的有序排列，功能相近的神经元非常靠近，功能不同的神经元离的较远。这一特点与人脑神经元的组织原理十分相似。

二、SOFM网的拓扑结构与权值调整域

1. 拓扑结构

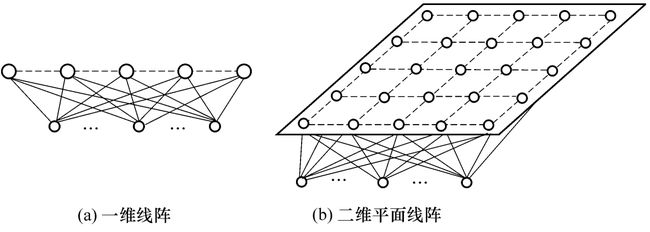
SOFM网共有两层，输入层个神经元通过权向量将外界信息汇集到输出层的个神经元。输入层的神经元数与样本维数相等。输出层为竞争网络中的竞争层。神经元的排列有多种形式，如一维线阵、二维平面阵和三维栅格阵，常见的是一维和二维。一维是最简单的，结构特点如下图所示，每个竞争层的神经元之间都有侧向连接。输出按照二维平面组织是SOFM网最典型的组织方式，更具有大脑皮层形象，输出层每个神经元同它周围的其他神经元侧向连接，排列成棋盘状平面，结构如下图右所示：

2. 权值调整域

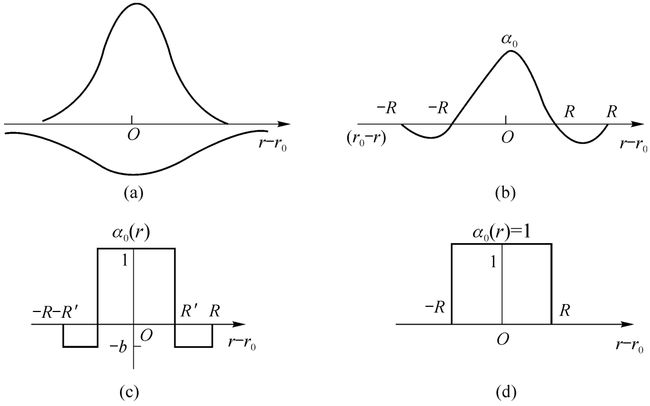
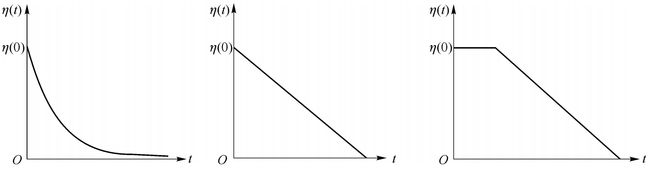
SOFM网采用的学习算法称为Kohonen算法，是在胜者为王算法基础上加以改进而成的，其主要的区别在于调整权向量与侧抑制的方式不同。在胜者为王学习规则中，只有竞争获胜神经元才能调整权向量，其他任何神经元都无权调整权向量，因此它对周围所有神经元的抑制是“封杀”式的。而SOFM网的获胜神经元对其学习算法中不仅获胜神经元本身要调整权向量，它周围的神经元在其影响下也要程度不同地调整权向量。这种调整可用下图所示的三种函数表示，其中（b）中的函数曲线是由（a）中的两个正态曲线组合而成的。

b-d中的3中函数沿中心轴旋转后可形成形状似帽子的空间曲面，按顺序分别为墨西哥帽函数、大礼帽函数和厨师帽函数。墨西哥帽函数是Kohonen提出的，它表明获胜神经元有最大的权值调整量，邻近的神经元有稍小的调整量，离获胜神经元距离越大，权的调整量越小，直到某一距离R时，权值调整量为0,。当距离再远一些时，权值调整量略负，更远时又回到0。墨西哥帽函数表现出的特点与生物系统的十分相似，但计算上的复杂性影响了网络训练的收敛性。因此，在SOFM网络中常使用与墨西哥函数类似的简化函数，如大礼帽函数和进一步简化后的厨师帽函数。

以获胜神经元为中心设定一个邻域半径，该半径圈定的范围称为优胜邻域。在SOFM网学习网络算法中，优胜邻域内所有神经元均按其离开获胜神经元的距离远近不同程度地调整权值。优胜邻域开始定得很大，但其大小随着训练次数的增加不断收缩，最终收缩到半径为零。

三、自组织特征映射网的运行原理与学习算法

1. 运行原理

SOFM网的运行分训练和工作两个阶段。在训练阶段，对网络随机输入训练集中的样本，对某个特定的输入模式，输出层会有某个神经元产生最大响应而获胜，而在训练开始阶段，输出层哪个位置的神经元将对那类输入模式产生最大响应是不确定的。当输入模式的类别改变时，二维平面的获胜神经元也会改变。获胜神经元周围的神经元因侧向相互兴奋作用产生较大响应，于是获胜神经元以及其优胜邻域内的所有神经元所连接的权向量均向输入向量的方向作程度不同的调整，调整力度依邻域内各神经元距获胜神经元的远近而逐渐衰减。网络通过自组织方式，用大量训练样本调整网络的权值，最后使输出层各神经元成为特定模式类敏感的神经细胞，对应的内星权向量成为各输入模式类的中心向量。并且当两个模式类的特征接近时，代表这两类的神经元在位置也接近。从而在输出层形成能够反映样本模式类分布情况的有序特征图。

SOFM网训练结束后，输出层各神经元与各输入模式类的特定关系就完全确定了，因此可用作模式分类器。当输入一个模式时，网络输出层代表该模式类的特定神经元将产生最大响应，从而将该输入自动归类。应当指出的是，当向网络输入的模式不属于网络训练时见过的任何模式类时，SOFM网只能将它归入最接近的模式类。

2. 学习算法

Kohonen算法

（1）初始化

对输出层各权向量赋值小随机数，并进行归一化处理。建立初始优胜邻域；学习率赋值初始值。

（2） 接受输入

从训练集中随机选取一个输入模式并进行归一化处理。

（3） 寻找获胜神经元

计算输入模式与内星权向量的点积，从中选出点积最大的获胜神经元；

（4） 定义优胜邻域

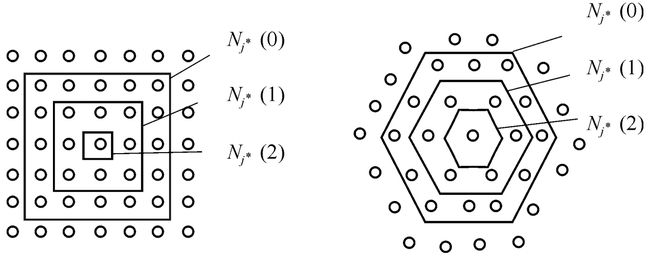
以获胜神经元为中心确定t时刻的权值调整域，一般初始邻域N较大，训练过程中N随着训练时间逐渐收缩。示意图如下所示：

（5） 调整权值

对优胜邻域内所有神经元调整权值。如下图：

式中，η（t，N）是训练时间t和邻域内第j个神经元与获胜神经元j*之间的拓扑距离N的函数，该函数一般有以下规律：

t ↑ → η↓ ，N↑ → η ↓

很多函数都能满足以上规律，例如可构造如下函数：

η（t）可采用t的单调下降函数，如下图所示，这种随着时间单调下降的函数称为退火函数。

（6） 结束检查

SOFM网的训练不存在类似BP网中输出误差概念，因为是非监督学习，训练何时结束时以学习速率η（t）是否衰减到0或某个预定的正小数为条件，不满足结束条件则回到步骤（2）。

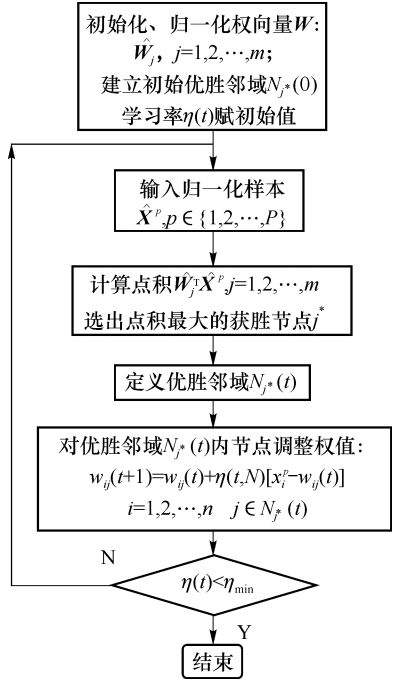
完整的流程如下图所示：

3. 功能分析

(1) 功能一:保序映射

SOFM网的功能特点之一是保序映射，即能将输入空间的样本模式类有序地映射在输出层。

下面举例说明：

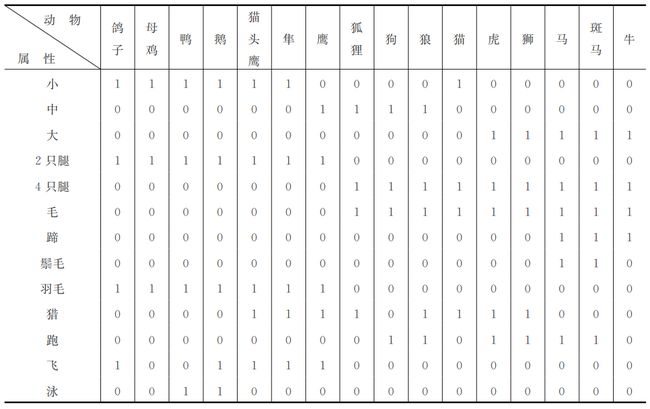
将不同动物按其属性特征映射到两维输出平面上，使得相似的动物在SOFM网输出平面上的位置也相近。该训练集16种动物，每种动物用29维向量表示，其中前16个分量构成符号向量，对不同的动物进行16取1编码，后13个分量构成属性向量，描述动物的13种属性，用1或0表示某种动物属性的有或无。如下表所示：

SOFM网的输出平面有10x10个神经元，用16个动物模式轮番输入进行训练，最后输出平面出现如下图所示的情况，可以看出属性相似的动物在输出平面上的位置相邻，实现了特征的保序分布。

(2) 功能二:数据压缩

SOFM网的功能特点之二是数据压缩。

数据压缩是将高纬空间的样本在保持拓扑结构不变的条件下映射到低纬空间。在这方面，SOFM网具有明显的优势。无论输入样本空间是多少维的，其模式样本都可以在SOFM网输出层的某个区域得到响应。SOFM网经过训练后，在高维空间相近的输入样本，其输出层响应神经元的位置也接近。因此对于任意n维输入空间的样本，均可通过映射到SOFM网的一维或二维输出层上完成数据压缩。如上例中的输入样本空间为29维，通过SOFM网后压缩为二维平面的数据。

（3）功能三:特征抽取

SOFM网的功能之三是特征抽取。

从特征抽取的角度看高纬空间样本向低维空间的映射，SOFM网的输出层相当于低维特征空间。在高维模式空间，很多模式的分布具有复杂的结构，从数据观测很难发现其内在规律。当通过SOFM网络映射到低维输出空间后，其规律往往一目了然，因此这种映射就是一种特征抽取。高维空间的向量经过特征抽取后可以在低维特征空间更加清晰地表达，因此映射的意义不仅仅是单纯的数据压缩，更是一种规律发现。

下面通过字符排序为例进行分析：

用32个字符作为SOFM网的输入样本，包括26个英文字母和6个数字（1-6）。每个字符对应于五维向量，各字符与相应向量X的5个分量的对应关系如下表所示：

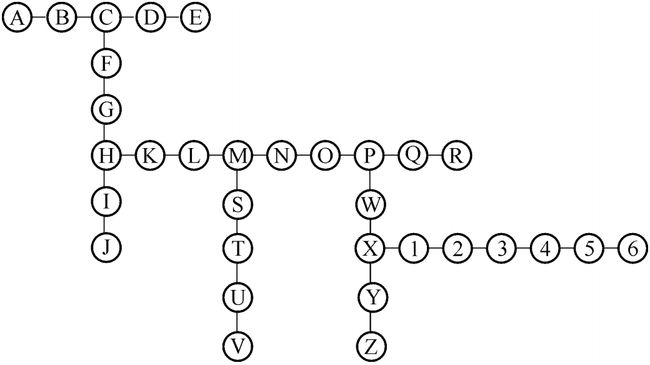
从表中可以看出代表A-B-C-D-E的各个向量中有四个分量是相同的，因此代表一类，以此类推，可将对应的字符标在下图所示的树形结构图中：

SOFM网络输出阵列为二维平面阵，该阵列由70个神经元组成，每个神经元用五维内星权向量与五维输入模式相连。将训练集中代表各字符的输入向量X随机送入网络中进行训练，经过10000步训练，各权向量趋于稳定，此时可对该网络输出进行校准，即根据输出阵列神经元与训练集的已知模式向量的对应关系贴标号。例如当输入向量B时，输出平面的左上角神经元在整个阵列中产生最强的响应，于是该神经元被标为B。在输出层的70个神经元中，有32个神经元有标号，而另外38个为未用神经元。

下图为通过自组织学习后的输出结果。SOFM网完成训练后，对每个输入字符，输出平面都有一个特定的神经元对其最为敏感，这种输入-输出的映射关系在输出特征平面中表现得非常清楚。SOFM网输出平面各个字符之间的位置关系与上图树形结构相当类似，两者结构特征上的一致性是非常明显的。输出平面上的点号“·”表示处于自由状态的神经元，它们对任何输入样本都不发生兴奋。

*********************************

2015-8-14

艺少