对偶传播神经网络（CPN）

1987年，美国学者Robert Hecht-Nielsen提出了对偶传播神经网络模型 （Counter Propagation Network，CPN），CPN最早是用来实现样本选择匹配系统的。CPN 网能存储二进制或模拟值的模式对，因此这种网络模型也可用于联想存储、模式分类、函数逼近、统计分析和数据压缩等用途。

1.    网络结构与运行原理

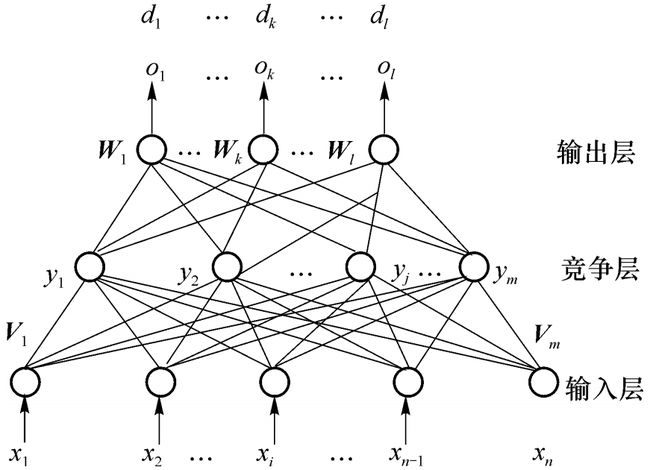
网络结构如图所示，各层之间的神经元全互联连接。从拓扑结构看，CPN网与三层BP网络相近，但实际上CPN是由自组织网和Grossberg外星网组合而成。隐层为竞争层，采用无导师的竞争学习规则，而输出层为Grossberg层，采用有导师信号的Widrow-Hoff规则或Grossberg规则学习。

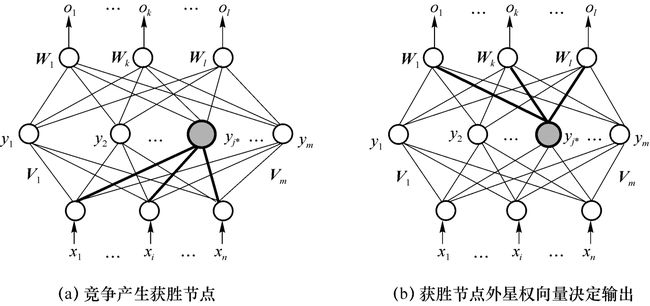
网络各层按两种学习规则训练好之后，运行阶段首先向网络送入输入变量，隐含层对这些输入进行竞争计算，获胜者成为当前输入模式类的代表，同时该神经元成为如下图(a)所示的活跃神经元，输出值为1而其余神经元处于非活跃状态，输出值为0。竞争取胜的隐含神经元激励输出层神经元，使其产生如下图(b)所示的输出模式。由于竞争失败的神经元输出为0，不参与输出层的整合。因此输出就由竞争胜利的神经元的外星权重确定。

2.    学习算法

网络学习分为两个阶段：第一阶段是竞争学习算法对隐含层神经元的内星权向量进行训练；第二阶段是采用外星学习算法对隐含层的神经元的外星权向量进行训练。

因为内星权向量采用的是竞争学习规则，跟前几篇博文所介绍的算法步骤基本类似，这里不做介绍，值得说明的是竞争算法并不设置优胜临域，只对获胜神经元的内星权向量进行调节。

下面重点介绍一下外星权向量的训练步骤:

（1）   输入一个模式以及对应的期望输入，计算网络隐节点净输入，隐节点的内星权向量采用上一阶段中训练结果。

（2）   确定获胜神经元使其输出为1。

（3）   调整隐含层到输出层的外星权向量，调整规则如下：

β为外星规则学习速率，为随时间下降的退火函数。O(t)为输出层神经元的输出值。

    由以上规则可知，只有获胜神经元的外星权向量得到调整，调整的目的是使外星权向量不断靠近并等于期望输出，从而将该输出编码到外星权向量中。

3.    改进CPN网

（1）   双获胜神经元CPN

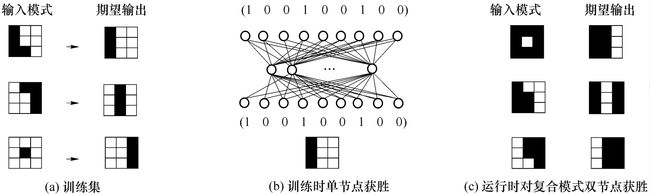
指的是在完成训练后的运行阶段允许隐层有两个神经元同时竞争获得胜利，这两个获胜神经元均取值为1，其他神经元则取值为0。于是有两个获胜神经元同时影响网络输出。下图给出了一个例子，表明了CPN网能对复合输入模式包含的所有训练样本对应的输出进行线性叠加，这种能力对于图像的叠加等应用十分合适。

（2）   双向CPN网

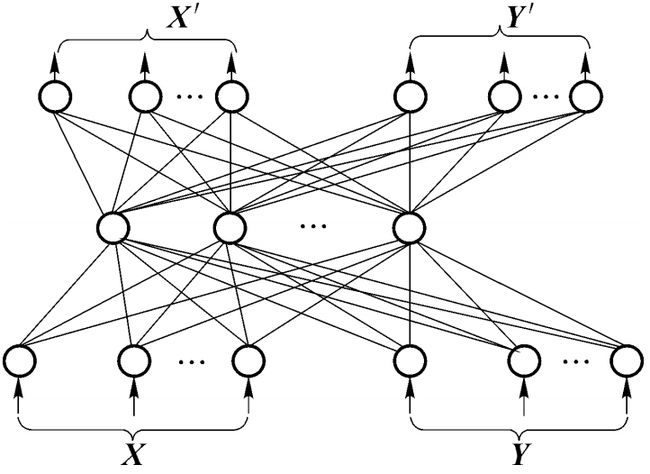
将CPN网的输入层和输出层各自分为两组，如下图所示。双向CPN网的优点是可以同时学习两个函数，例如：Y＝f （X）；X′＝f （Y′）

当两个函数互逆时，有X ＝X′，Y ＝Y′。双向CPN可用于数据压缩与解压缩，可将其中一个函数f作为压缩函数，将其逆函数g作为解压缩函数。

事实上，双向CPN网并不要求两个互逆函数是解析表达的，更一般的情况是f和g是互逆的映射关系，从而可利用双向CPN实现互联想。

4.    CPN网应用

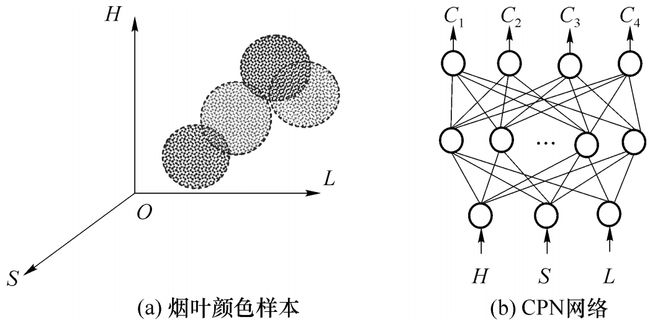
下图给出了CPN网用于烟叶颜色模式分类的情况，输入样本分布在下图(a)所示的三维颜色空间中，该空间的每个点用一个三维向量表示，各分量分别代表烟叶的平均色调H，平均亮度L和平均饱和度S。可以看出颜色模式分为4类，分别对应红棕色，橘黄色，柠檬色和青黄色。下图(b)给出了CPN网络结构，隐层共设了10个神经元，输出层设4个神经元，学习速率为随训练时间下降的函数，经过2000次递归之后，网络分类的正确率达到96%。

 

 *************************************

2015-8-15

艺少