GDAL使用DEM数据计算山体阴影（Hillshade）

零、        前言

说起Hillshade，其实就是模拟太阳光照射地形所引起的明暗对比，然后来对地形图进行渲染，使之看起来具有立体效果的一种方式，常用于地图的渲染，如表1所示，具体的可以参考文献[1]，表1中的图均来自参考文献[1]。

表1 DEM、山体阴影以及应用对比

DEM图像（使用颜色渲染）	从左图的DEM图像中计算的山体阴影图
Paper Map Without Hillshade	Paper Map With Hillshade
Satellite Image Without Hillshade	Satellite Image With Hillshade

从表1中的图可以看出，使用山体阴影对地图和卫星图像进行渲染后，视觉效果得到了很大的提升，具有很明显的立体感。下面就对如何实现山体阴影进行一个说明。

一、        山体阴影原理简介

山体阴影通过为栅格中的每个像元指定太阳高度等信息，来计算表面的假定亮度值。通过设置假定光源的位置和计算与相邻像元相关的每个像元的亮值，即可得出假定亮度度。进行分析或图形显示时，特别是使用透明度后，“山体阴影”可大大增强表面的可视化。

默认情况下，阴影和光线是与介于 0 和 255 之间的整数相关的灰度梯度（从黑色渐变为白色）。【摘自参考文献[4,5]】。

山体阴影计算的时候，需要指定太阳在天空中的位置，这个位置可以用下面两个参数来进行描述。

1、太阳方位角

太阳方向角指的是太阳的角度方向，是以北为基准方向，在0度到360度范围内按顺时针进行测量的。90º的方位角为东。默认方向角为 315º (NW，西北方向)。如图1所示，图中黄色圆圈代表太阳。

2、太阳高度角

太阳高度角指的是太阳高出地平线的角度或坡度。高度的单位为度，范围为0度（位于地平线上）到 90度（位于头顶上）之间。默认值为45度。如图2所示，途中黄色圆圈代表太阳。

               

图1 太阳方位角示意图                图2 太阳高度角示意图

二、        计算方法

在计算山体阴影的公式如式（1）所示，详情参考文献[6]。式（1）中的Zenith表示太阳天顶角，Azimuth表示太阳方位角，Slope和Aspect分别表示坡度和坡向。后缀_rad表示所有的角度都是以弧度为单位的。

 Hillshade = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) + (sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad)))（1）

通过上式计算山体阴影时，计算的结果可能是小于0的值，此时应该将该值设置为0。下面对计算山体阴影的过程进行拆分说明，主要有下面几个步骤：

1、计算太阳入射角度

指定太阳的高度角必须大于地平线的角度（也就是0度）。但是，用于计算山体阴影值的公式要求以弧度为单位表示角度并且要求是从垂直方向偏转的角度。将垂直于地表面的方向（头顶正上方）标注为天顶。天顶角是从天顶点到太阳的方向测之间的角度，也就是太阳高度角的余角（即90度减去太阳高度角）。要计算太阳入射角度，第一步是将太阳高度角转换为天顶角。第二步是将天顶角转换为弧度。

将太阳高度角转换为天顶角：

Zenith_deg = 90 - Altitude   （2）

转换为弧度：

Zenith_rad = Zenith * pi / 180.0  （3）

2、计算太阳方位角

山体阴影公式要求方位角采用弧度作为单位。首先，将天顶角从地理单位（罗盘方向）转换为数学单位（直角）。然后再将方位角转换为弧度。具体见公式（4）（5）（6）。

转换太阳方位角的方法：

Azimuth_math = 360.0 - Azimuth + 90  (4)

请注意，如果，Azimuth_math >= 360.0 则：

Azimuth_math = Azimuth_math - 360.0  (5)

转换为弧度：

   Azimuth_rad = Azimuth_math * pi / 180.0   (6)

3、计算坡度坡向

关于坡度坡向的计算方法这里就不说了，可以参考前面两篇博客，具体参考这里《GDAL使用DEM数据计算坡度坡向》，参考文献[7]。需要注意的是，要将计算的坡度和坡向转为弧度单位。

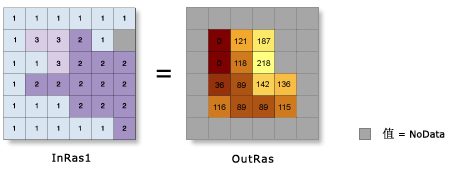
至此，所有的变量都计算出来了，然后带入公式（1）即可求得山体阴影的值。图3是一个山体阴影计算的示意图，太阳方位角为99度，太阳高度角为33度的计算结果。

图3 山体阴影计算示例

三、        算法编写

由于计算山体阴影还是一个3×3的窗口，所以我们继续用之前的那个3×3的算法作为基础，这里只实现算法部分即可。在计算的过程中需要考虑到像元的大小和高程的单位，如果两者的单位不一致，需要做一个转换，此外还有的时候需要对高程进行一个夸大，目的是为了更突出地形信息。

首先是山体阴影的算法结构体，在算法结构体中对输入的参数提前进行了一系列的处理，比如角度直接计算出正弦和余弦值，这样就会在后面的算法中直接使用，而不用再次计算，提高算法的效率，当然都是些小的细节问题。

/**
* @brief 山体阴影算法结构体
*/
typedef struct
{
         /*! 南北方向分辨率 */
         double nsres;
         /*! 东西方向分辨率 */
         double ewres;
         /*! 方位角的正弦值 */
         doublesin_altRadians;
         /*! 方位角的余弦值乘以Z缩放比 */
         doublecos_altRadians_mul_z_scale_factor;
         /*! 太阳高度角 */
         doubleazRadians;
         /*! z缩放比平方 */
         doublesquare_z_scale_factor;
} GDALHillshadeAlgData;

接下来是算法实现函数，这个函数基本就是按照上面的公式来写的，没啥难度。

float GDALHillshadeAlg (float* afWin, floatfDstNoDataValue, void* pData)
{
         GDALHillshadeAlgData*psData = (GDALHillshadeAlgData*)pData;
         double x, y,aspect, xx_plus_yy, cang;
 
         // 计算坡度
         x =((afWin[0] + afWin[3] + afWin[3] + afWin[6]) -
                   (afWin[2]+ afWin[5] + afWin[5] + afWin[8])) / psData->ewres;
 
         y =((afWin[6] + afWin[7] + afWin[7] + afWin[8]) -
                   (afWin[0]+ afWin[1] + afWin[1] + afWin[2])) / psData->nsres;
 
         xx_plus_yy =x * x + y * y;
 
         // 计算坡向
         aspect =atan2(y, x);
 
         // 计算山体阴影值
         cang =(psData->sin_altRadians -
                   psData->cos_altRadians_mul_z_scale_factor* sqrt(xx_plus_yy) *
                   sin(aspect- psData->azRadians)) /
                   sqrt(1+ psData->square_z_scale_factor * xx_plus_yy);
 
         if (cang<= 0.0)
                   cang= 1.0;
         else
                   cang= 1.0 + (254.0 * cang);
 
         return(float)cang;
}

最后还需要一个创建算法所需参数的一个函数，这个函数输入的有图像的六参数，用于获取图像的分辨率；z是高程的缩放比例，就是有的时候地形比较平坦，出来的效果不太好，可以使用z值来进行一个夸大；sacle是水平像素单位和高程单位的一个换算系数，有的时候像素单位是按照经纬度的，而高程单位一般是米，这时就需要设置sacle了；最后两个参数就是上面说的方位角和高度角。

void* GDALCreateHillshadeData(double* adfGeoTransform,
                                                                    double z,
                                                                    double scale,
                                                                    double alt,
                                                                    double az)
{
         GDALHillshadeAlgData*pData =
                   (GDALHillshadeAlgData*)CPLMalloc(sizeof(GDALHillshadeAlgData));
 
         const doubledegreesToRadians = M_PI / 180.0;
         pData->nsres= adfGeoTransform[5];
         pData->ewres= adfGeoTransform[1];
         pData->sin_altRadians= sin(alt * degreesToRadians);
         pData->azRadians= az * degreesToRadians;
         doublez_scale_factor = z / (8 * scale);
         pData->cos_altRadians_mul_z_scale_factor=
                   cos(alt* degreesToRadians) * z_scale_factor;
         pData->square_z_scale_factor= z_scale_factor * z_scale_factor;
         return pData;
}

最后在网上有一个使用Matlab编写的计算山体阴影的m文件，具体参考文献[2]。有兴趣的可以下载下来用Matlab试试。

四、        处理结果

最后没啥好说的，贴张处理后的图给大家看看（方位角为315度，高度角为45度）。希望对大家有用。

图4 DEM数据

图5 DEM渲染后的数据

图5 高程缩放为1时的效果

图5 高程缩放为2时的效果

图4 高程缩放为10时的效果

五、        参考文献

[1] http://www.gichd.org/fileadmin/pdf/IMSMA/fact-sheets/GICHDFactSheet-Hillshade%20Imagery.PDF(Hillshade的一个说明)

[2] http://www.mathworks.ch/matlabcentral/fileexchange/14863-hillshade/content/hillshade.m(MatLab的版本)

[3]http://download.osgeo.org/ossim/tutorials/pdfs/HillShade.pdf（OSSIM软件中的使用说明）

[4]http://help.arcgis.com/en/arcgisdesktop/10.0/help/index.html#/na/009z000000v0000000/

[5]http://help.arcgis.com/en/arcgisdesktop/10.0/help/index.html#/How_Hillshade_works/009z000000z2000000/

[6]Burrough, P. A. and McDonell, R. A.,1998. Principles of Geographical Information Systems (OxfordUniversity Press, New York), 190 pp.

[7] http://blog.csdn.net/liminlu0314/article/details/8498985（GDAL计算坡度坡向）

[8] http://www.aubreyrhea.net/gis/index.php/tag/hillshade/（ArcMap软件中的使用说明）