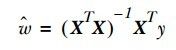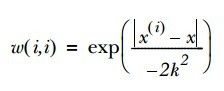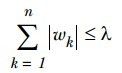机器学习理论与实战（八）回归

       按照《机器学习实战》的主线，结束有监督学习中关于分类的机器学习方法，进入回归部分。所谓回归就是数据进行曲线拟合，回归一般用来做预测，涵盖线性回归（经典最小二乘法）、局部加权线性回归、岭回归和逐步线性回归。先来看下线性回归，即经典最小二乘法，说到最小二乘法就不得说下线性代数，因为一般说线性回归只通过计算一个公式就可以得到答案，如（公式一）所示：

（公式一）

       其中X是表示样本特征组成的矩阵，Y表示对应的值，比如房价，股票走势等，（公式一）是直接通过对（公式二）求导得到的，因为（公式二）是凸函数，导数等于零的点就是最小点。

（公式二）

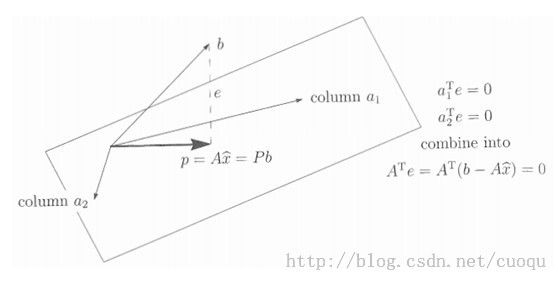
         不过并不是所有的码农能从（公式二）求导得到（公式一）的解，因此这里给出另外一个直观的解，直观理解建立起来后，后续几个回归就简单类推咯。从初中的投影点说起，如（图一）所示：

（图一）

       在（图一）中直线a上离点b最近的点是点b在其上的投影，即垂直于a的交点p。p是b在a上的投影点。试想一下，如果我们把WX看成多维的a,即空间中的一个超面来代替二维空间中的直线，而y看成b,那现在要使得（公式二）最小是不是就是寻找（图一）中的e,即垂直于WX的垂线，因为只有垂直时e才最小。下面来看看如何通过寻找垂线并最终得到W。要寻找垂线，先从（图二）中的夹角theta 说起吧，因为当cos(theta)=0时，他们也就垂直了。下面来分析下直线或者向量之间的夹角，如（图二）所示：

（图二）

       在（图二）中， 表示三角形 的斜边，那么：

       角beta也可以得到同样的计算公式，接着利用三角形和差公式得到（公式三）：

（公式三）

        （公式三）表示的是两直线或者两向量之间的夹角公式，很多同学都学过。再仔细看下，发现分子其实是向量a,b之间的内积（点积），因此公式三变为简洁的（公式四）的样子：

（公式四）

接下来继续分析（图一）中的投影，为了方便观看，增加了一些提示如（图三）所示：

（图三）

        在（图三）中，假设向量b在向量a中的投影为p（注意，这里都上升为向量空间，不再使用直线，因为（公式四）是通用的）。投影p和a 在同一方向上（也可以反方向），因此我们可以用一个系数乘上a来表示p,比如（图三）中的 ，有了投影向量p，那么我们就可以表示向量e,因为根据向量法则， ，有因为a和e垂直，因此 ，展开求得系数x,如（公式五）所示：

（公式五）

（公式五）是不是很像（公式一）？只不过（公式一）的分母写成了另外的形式，不过别急，现在的系数只是一个标量数字，因为a,b都是一个向量，我们要扩展一下，把a从向量扩展到子空间，因为（公式一）中的X是样本矩阵，矩阵有列空间和行空间，如（图四）所示：

（图四）

        （图四）中的A表示样本矩阵X，假设它有两个列a1和a2,我们要找一些线性组合系数来找一个和（图三）一样的接受b 投影的向量，而这个向量通过矩阵列和系数的线性组合表示。求解的这个系数的思路和上面完全一样，就是寻找投影所在的向量和垂线e的垂直关系，得到系数，如（公式六）所示：

（公式六）

       这下（公式六）和（公式一）完全一样了，基于最小二乘法的线性回归也就推导完成了，而局部加权回归其实只是相当于对不同样本之间的关系给出了一个权重，所以叫局部加权，如（公式七）所示：

（公式七）

       而权重的计算可通过高斯核（高斯公式）来完成，核的作用就是做权重衰减，很多地方都要用到，表示样本的重要程度，一般离目标进的重要程度大些，高斯核可以很好的描述这种关系。如（公式八）所示，其中K是个超参数，根据情况灵活设置：

（公式八）

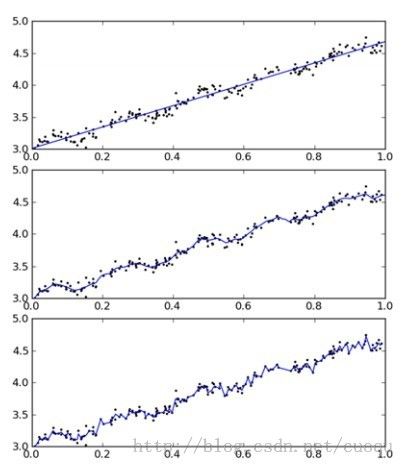
       （图五）是当K分别为1.0, 0.01,0.003时的局部加权线性回归的样子，可以看出当K=1.0时，和线性回归没区别：

（图五）

  而岭回归的样子如（公式九）所示：

（公式九）

        岭回归主要是解决的问题就是当XX’无法求逆时，比如当特征很多，样本很少，矩阵X不是满秩矩阵，此时求逆会出错，但是通过加上一个对角为常量lambda的矩阵，就可以很巧妙的避免这个计算问题，因此会多一个参数lambda,lambda的最优选择由交叉验证（cross-validation）来决定，加上一个对角不为0的矩阵很形象的在对角上抬高了，因此称为岭。不同的lambda会使得系数缩减，如（图六）所示：

（图六）

         说到系数缩减大家可能会觉得有奇怪，感觉有点类似于正则，但是这里只是相当于在（公式六）中增大分母，进而缩小系数，另外还有一些系数缩减的方法，比如直接增加一些约束，如（公式十）和（公式十一）所示：

（公式十）

（公式十一）

        当线性回归增加了（公式十）的约束变得和桥回归差不多，系数缩减了，而如果增加了（公式十一）的约束时就是稀疏回归咯，（我自己造的名词，sorry）,系数有一些0。

有了约束后，求解起来就不像上面那样直接计算个矩阵运算就行了，回顾第五节说中支持向量机原理，需要使用二次规划求解，不过仍然有一些像SMO算法一样的简化求解算法，比如前向逐步回归方法：

前向逐步回归的伪代码如（图七）所示，也不难，仔细阅读代码就可以理解：

（图七）

 

     下面直接给出上面四种回归的代码：

     

from numpy import *

def loadDataSet(fileName):      #general function to parse tab -delimited floats
    numFeat = len(open(fileName).readline().split('\t')) - 1 #get number of fields 
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat,labelMat

def standRegres(xArr,yArr):
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T*xMat
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T*yMat)
    return ws

def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye((m)))
    for j in range(m):                      #next 2 lines create weights matrix
        diffMat = testPoint - xMat[j,:]     #
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws

def lwlrTest(testArr,xArr,yArr,k=1.0):  #loops over all the data points and applies lwlr to each one
    m = shape(testArr)[0]
    yHat = zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat

def lwlrTestPlot(xArr,yArr,k=1.0):  #same thing as lwlrTest except it sorts X first
    yHat = zeros(shape(yArr))       #easier for plotting
    xCopy = mat(xArr)
    xCopy.sort(0)
    for i in range(shape(xArr)[0]):
        yHat[i] = lwlr(xCopy[i],xArr,yArr,k)
    return yHat,xCopy

def rssError(yArr,yHatArr): #yArr and yHatArr both need to be arrays
    return ((yArr-yHatArr)**2).sum()

def ridgeRegres(xMat,yMat,lam=0.2):
    xTx = xMat.T*xMat
    denom = xTx + eye(shape(xMat)[1])*lam
    if linalg.det(denom) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = denom.I * (xMat.T*yMat)
    return ws
    
def ridgeTest(xArr,yArr):
    xMat = mat(xArr); yMat=mat(yArr).T
    yMean = mean(yMat,0)
    yMat = yMat - yMean     #to eliminate X0 take mean off of Y
    #regularize X's
    xMeans = mean(xMat,0)   #calc mean then subtract it off
    xVar = var(xMat,0)      #calc variance of Xi then divide by it
    xMat = (xMat - xMeans)/xVar
    numTestPts = 30
    wMat = zeros((numTestPts,shape(xMat)[1]))
    for i in range(numTestPts):
        ws = ridgeRegres(xMat,yMat,exp(i-10))
        wMat[i,:]=ws.T
    return wMat

def regularize(xMat):#regularize by columns
    inMat = xMat.copy()
    inMeans = mean(inMat,0)   #calc mean then subtract it off
    inVar = var(inMat,0)      #calc variance of Xi then divide by it
    inMat = (inMat - inMeans)/inVar
    return inMat

def stageWise(xArr,yArr,eps=0.01,numIt=100):
    xMat = mat(xArr); yMat=mat(yArr).T
    yMean = mean(yMat,0)
    yMat = yMat - yMean     #can also regularize ys but will get smaller coef
    xMat = regularize(xMat)
    m,n=shape(xMat)
    #returnMat = zeros((numIt,n)) #testing code remove
    ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy()
    for i in range(numIt):
        print ws.T
        lowestError = inf; 
        for j in range(n):
            for sign in [-1,1]:
                wsTest = ws.copy()
                wsTest[j] += eps*sign
                yTest = xMat*wsTest
                rssE = rssError(yMat.A,yTest.A)
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        #returnMat[i,:]=ws.T
    #return returnMat

#def scrapePage(inFile,outFile,yr,numPce,origPrc):
#    from BeautifulSoup import BeautifulSoup
#    fr = open(inFile); fw=open(outFile,'a') #a is append mode writing
#    soup = BeautifulSoup(fr.read())
#    i=1
#    currentRow = soup.findAll('table', r="%d" % i)
#    while(len(currentRow)!=0):
#        title = currentRow[0].findAll('a')[1].text
#        lwrTitle = title.lower()
#        if (lwrTitle.find('new') > -1) or (lwrTitle.find('nisb') > -1):
#            newFlag = 1.0
#        else:
#            newFlag = 0.0
#        soldUnicde = currentRow[0].findAll('td')[3].findAll('span')
#        if len(soldUnicde)==0:
#            print "item #%d did not sell" % i
#        else:
#            soldPrice = currentRow[0].findAll('td')[4]
#            priceStr = soldPrice.text
#            priceStr = priceStr.replace('$','') #strips out $
#            priceStr = priceStr.replace(',','') #strips out ,
#            if len(soldPrice)>1:
#                priceStr = priceStr.replace('Free shipping', '') #strips out Free Shipping
#            print "%s\t%d\t%s" % (priceStr,newFlag,title)
#            fw.write("%d\t%d\t%d\t%f\t%s\n" % (yr,numPce,newFlag,origPrc,priceStr))
#        i += 1
#        currentRow = soup.findAll('table', r="%d" % i)
#    fw.close()
    
from time import sleep
import json
import urllib2
def searchForSet(retX, retY, setNum, yr, numPce, origPrc):
    sleep(10)
    myAPIstr = 'AIzaSyD2cR2KFyx12hXu6PFU-wrWot3NXvko8vY'
    searchURL = 'https://www.googleapis.com/shopping/search/v1/public/products?key=%s&country=US&q=lego+%d&alt=json' % (myAPIstr, setNum)
    pg = urllib2.urlopen(searchURL)
    retDict = json.loads(pg.read())
    for i in range(len(retDict['items'])):
        try:
            currItem = retDict['items'][i]
            if currItem['product']['condition'] == 'new':
                newFlag = 1
            else: newFlag = 0
            listOfInv = currItem['product']['inventories']
            for item in listOfInv:
                sellingPrice = item['price']
                if  sellingPrice > origPrc * 0.5:
                    print "%d\t%d\t%d\t%f\t%f" % (yr,numPce,newFlag,origPrc, sellingPrice)
                    retX.append([yr, numPce, newFlag, origPrc])
                    retY.append(sellingPrice)
        except: print 'problem with item %d' % i
    
def setDataCollect(retX, retY):
    searchForSet(retX, retY, 8288, 2006, 800, 49.99)
    searchForSet(retX, retY, 10030, 2002, 3096, 269.99)
    searchForSet(retX, retY, 10179, 2007, 5195, 499.99)
    searchForSet(retX, retY, 10181, 2007, 3428, 199.99)
    searchForSet(retX, retY, 10189, 2008, 5922, 299.99)
    searchForSet(retX, retY, 10196, 2009, 3263, 249.99)
    
def crossValidation(xArr,yArr,numVal=10):
    m = len(yArr)                           
    indexList = range(m)
    errorMat = zeros((numVal,30))#create error mat 30columns numVal rows
    for i in range(numVal):
        trainX=[]; trainY=[]
        testX = []; testY = []
        random.shuffle(indexList)
        for j in range(m):#create training set based on first 90% of values in indexList
            if j < m*0.9: 
                trainX.append(xArr[indexList[j]])
                trainY.append(yArr[indexList[j]])
            else:
                testX.append(xArr[indexList[j]])
                testY.append(yArr[indexList[j]])
        wMat = ridgeTest(trainX,trainY)    #get 30 weight vectors from ridge
        for k in range(30):#loop over all of the ridge estimates
            matTestX = mat(testX); matTrainX=mat(trainX)
            meanTrain = mean(matTrainX,0)
            varTrain = var(matTrainX,0)
            matTestX = (matTestX-meanTrain)/varTrain #regularize test with training params
            yEst = matTestX * mat(wMat[k,:]).T + mean(trainY)#test ridge results and store
            errorMat[i,k]=rssError(yEst.T.A,array(testY))
            #print errorMat[i,k]
    meanErrors = mean(errorMat,0)#calc avg performance of the different ridge weight vectors
    minMean = float(min(meanErrors))
    bestWeights = wMat[nonzero(meanErrors==minMean)]
    #can unregularize to get model
    #when we regularized we wrote Xreg = (x-meanX)/var(x)
    #we can now write in terms of x not Xreg:  x*w/var(x) - meanX/var(x) +meanY
    xMat = mat(xArr); yMat=mat(yArr).T
    meanX = mean(xMat,0); varX = var(xMat,0)
    unReg = bestWeights/varX
    print "the best model from Ridge Regression is:\n",unReg
    print "with constant term: ",-1*sum(multiply(meanX,unReg)) + mean(yMat)

以上各种回归方法没有考虑实际数据的噪声，如果噪声很多，直接用上述的回归不是太好，因此需要加上正则，然后迭代更新权重

参考文献：

         [1] machine learning in action.Peter Harrington 

       [2]Linear Algebra and Its Applications_4ed.Gilbert_Strang

转载请注明来源：http://blog.csdn.net/cuoqu/article/details/9387305