斯坦福大学公开课 :机器学习课程(Andrew Ng)——13、无监督学习:Principal Component Analysis (PCA)
1)问题起源
2)主成分分析Principal Component Analysis (PCA)
2.0)主成分分析理论基础——最大方差理论
2.1)主成分分析预处理2.2)主成分分析举例说明
3)总结和讨论
1)问题起源
真实的训练数据总是存在各种各样的问题:
1、 比如拿到一个汽车的样本,里面既有以“千米/每小时”度量的最大速度特征,也有“英里/小时”的最大速度特征,显然这两个特征有一个多余。
2、 拿到一个数学系的本科生期末考试成绩单,里面有三列,一列是对数学的兴趣程度,一列是复习时间,还有一列是考试成绩。我们知道要学好数学,需要有浓厚的兴趣,所以第二项与第一项强相关,第三项和第二项也是强相关。那是不是可以合并第一项和第二项呢?
回顾我们之前介绍的《learning theory》中提到过Feature Selection,但在那篇中要剔除的特征主要是和类标签无关的特征。比如“学生的名字”就和他的“成绩”无关,使用的是互信息的方法。而这里的特征很多是和类标签有关的,但里面存在噪声或者冗余。在这种情况下,需要一种特征降维的方法来减少特征数,减少噪音和冗余,减少过度拟合的可能性。
下面探讨一种称作主成分分析(PCA)的方法来解决部分上述问题。PCA的思想是将n维特征映射到k维上(k<n),这k维是全新的正交特征。这k维特征称为主元,是重新构造出来的k维特征,而不是简单地从n维特征中去除其余n-k维特征。
2)主成分分析Principal Component Analysis (PCA)
2.0)主成分分析理论基础——最大方差理论
假设我们想要将原本n维的特征映射到k(k<n)维新的特征上,我们认为,最好的k个维度应该具有这样的性质:将n维特征样本点转换为k维特征样本点后,仅利用这k维特征仍然能够很好的区分样本点,即,映射后,原来数据之间的差异性仍然要尽可能大的保存,也就是说在k维特征上的每一维,样本方差都很大。
例如下面的图片,我们更希望按照第一幅图来映射:
对“映射”的理解可以参考下图:
红色点表示样例![]() ,蓝色点表示
,蓝色点表示![]() 在u上的投影,u是直线的斜率也是直线的方向向量,而且是单位向量。蓝色点是
在u上的投影,u是直线的斜率也是直线的方向向量,而且是单位向量。蓝色点是![]() 在u上的投影点,它离原点的距离是
在u上的投影点,它离原点的距离是![]() (即
(即![]() 或者
或者![]() )。由于红色样本点的每一维特征均值都为0(预处理过程会保证这一点,见下一节预处理部分介绍),因此投影到u上的样本点的均值仍然是0。
)。由于红色样本点的每一维特征均值都为0(预处理过程会保证这一点,见下一节预处理部分介绍),因此投影到u上的样本点的均值仍然是0。
回到上面左右图中的左图,我们要求的是最佳的u,使得投影后的样本点方差最大,即下面的式子取值最小(投影后均值为0):
中间那部分正是样本特征的协方差矩阵( 用![]() 来表示
来表示![]() ,
,![]() 表示
表示![]() ,那么上式写作
,那么上式写作![]() 。
。
由于u是单位向量,即![]() ,上式两边都左乘u得,
,上式两边都左乘u得,![]() ,即
,即![]() 。
。
![]() 告诉我们:
告诉我们: ![]() 就是
就是![]() 的特征值,u是特征向量。要想使上面的式子取值最大,即令
的特征值,u是特征向量。要想使上面的式子取值最大,即令![]() 取值最大,最佳的投影直线的单位向量u应该是特征值
取值最大,最佳的投影直线的单位向量u应该是特征值![]() 最大时对应的特征向量才好,其次是
最大时对应的特征向量才好,其次是![]() 第二大对应的特征向量,依次类推。
第二大对应的特征向量,依次类推。
其中的第j维就是![]() 在
在![]() 上的投影。通过选取最大的k个u,使得方差较小的特征(如噪声)被丢弃。
上的投影。通过选取最大的k个u,使得方差较小的特征(如噪声)被丢弃。
2.1)主成分分析预处理
第(1-2)步是让每个原始数据减去数据的均值,如果提前知道数据的均值为0(例如x服从正态分布时),可以省去(1-2)步。第(3-4)步是让每个坐标(训练样本的每个特征分量)有相同的方差(例如一个特征是汽车速度(0到100),一个是汽车的座位数(2到6),显然第二个的方差比第一个小,这是就很有必要预处理),如果提前知道不同的特征分量有相同的方差(例如每一个训练样本点都表示灰度图片,即每个特征分量只能取{0,1,...,255}时),可以省去(3-4)步。
2.2)主成分分析举例说明
原始数据(2维):
第一步,预处理(过程同上描述,但省略(3-4)步):
第二步,求训练样本的特征的协方差矩阵![]() =
= ![]()
对角线上分别是x和y的方差,非对角线上是协方差。协方差大于0表示x和y若有一个增,另一个也增;小于0表示一个增,一个减;协方差为0时,两者独立。协方差绝对值越大,两者对彼此的影响越大,反之越小。
第三步,求协方差矩阵的特征值和特征向量
上面是两个特征值,下面是对应的特征向量,特征值0.0490833989对应特征向量为![]() ,这里的特征向量都归一化为单位向量。
,这里的特征向量都归一化为单位向量。
第四步,选择前k大特征值对应的特征向量分别作为列向量组成特征向量矩阵
将特征值按照从大到小的顺序排序,选择其中最大的k个,然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。这里特征值只有两个,我们选择其中最大的那一个,这里是1.28402771,对应的特征向量是![]() 。
。
第五步,将样本点投影到选取的特征向量上
假设样例数为m,特征数为n,预处理之后的样本矩阵为DataAdjust(m*n),协方差矩阵是n*n,选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为
![]()
这里是
FinalData(10*1) = DataAdjust(10*2矩阵)×特征向量![]()
得到结果是
经过上面五步,就将原始样例的n维特征变成了k维,这k维就是原始特征在k维上的投影。整个PCA过程非常简单,就是求训练样本的特征的协方差矩阵3)总结和讨论
主成分分析除了可以通过最大方差理论进行推导,还可以使用点到直线的距离d’来度量,具体方法参考:http://www.cnblogs.com/jerrylead/archive/2011/04/18/2020216.html。
PCA技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序,根据需要取前面最重要的部分,将后面的维数省去,可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。
PCA技术的一个很大的优点是,它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。 但是,这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高。有一类根据先验知识对数据预先进行非线性转换的方法就成为kernel-PCA,它扩展了PCA能够处理的问题的范围,又可以结合一些先验约束,是比较流行的方法。
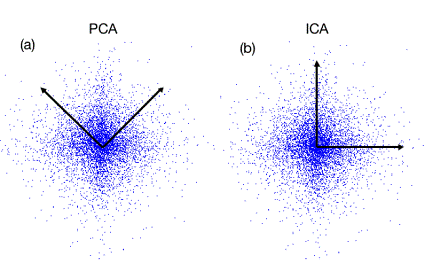
有时数据的分布并不是满足高斯分布。如下图所示,在非高斯分布的情况下,PCA方法得出的主元可能并不是最优的。在寻找主元时不能将方差作为衡量重要性的标准。要根据数据的分布情况选择合适的描述完全分布的变量,然后根据概率分布式![]() 来计算两个向量上数据分布的相关性。等价的,保持主元间的正交假设,寻找的主元同样要使
来计算两个向量上数据分布的相关性。等价的,保持主元间的正交假设,寻找的主元同样要使![]() 。这一类方法被称为独立主元分解(ICA)。
。这一类方法被称为独立主元分解(ICA)。
数据的分布并不满足高斯分布,呈明显的十字星状。 这种情况下,方差最大的方向并不是最优主元方向。
![clip_image028[4] 斯坦福大学公开课 :机器学习课程(Andrew Ng)——13、无监督学习:Principal Component Analysis (PCA)_第1张图片](http://img.e-com-net.com/image/info5/e517de517f9a4b69ad7f5bb933846fa3.jpg)

![clip_image042[4] 斯坦福大学公开课 :机器学习课程(Andrew Ng)——13、无监督学习:Principal Component Analysis (PCA)_第3张图片](http://img.e-com-net.com/image/info5/1748e690fd7f4e5f8eee784cb7db580c.jpg)
![clip_image059[4] 斯坦福大学公开课 :机器学习课程(Andrew Ng)——13、无监督学习:Principal Component Analysis (PCA)_第4张图片](http://img.e-com-net.com/image/info5/21df545a1663402ebe88b48771bef5f5.jpg)
![clip_image017[4] 斯坦福大学公开课 :机器学习课程(Andrew Ng)——13、无监督学习:Principal Component Analysis (PCA)_第5张图片](http://img.e-com-net.com/image/info5/7a46b72f931f4bbc959ae6a4b1222673.jpg)
![clip_image001[4] 斯坦福大学公开课 :机器学习课程(Andrew Ng)——13、无监督学习:Principal Component Analysis (PCA)_第6张图片](http://img.e-com-net.com/image/info5/c8adeeed6afb4dae90349990ed60c702.png)
![clip_image002[4] 斯坦福大学公开课 :机器学习课程(Andrew Ng)——13、无监督学习:Principal Component Analysis (PCA)_第7张图片](http://img.e-com-net.com/image/info5/da0aaab0b2324895a85a8489a0d76aa5.png)
![clip_image004[4] clip_image004[4]](http://img.e-com-net.com/image/info5/e65b2ceb3edf44cba56ec2cc9e57cd67.png)
![clip_image005[4] 斯坦福大学公开课 :机器学习课程(Andrew Ng)——13、无监督学习:Principal Component Analysis (PCA)_第8张图片](http://img.e-com-net.com/image/info5/9700d581e9b644b99e2b3269cc331216.png)
![clip_image012[4] 斯坦福大学公开课 :机器学习课程(Andrew Ng)——13、无监督学习:Principal Component Analysis (PCA)_第9张图片](http://img.e-com-net.com/image/info5/a67f877293e248a1be167af0e5cd9c9e.png)