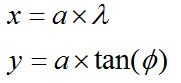理解墨卡托投影原理
背景介绍
墨卡托投影思想是GIS的基石,GPS设备采集的数据是标准的wgs84坐标,各家地图从数据提供商拿到的经纬度数据经过国测局gcj02加密的结果。地球的纬度不可能取到+-90,范围在-85-85。
地图数据处理、渲染都需要转化成平面的笛卡尔坐标系。而墨卡托投影则定义了如何从球面坐标系投影到二维的平面。二维的单位是米,也可以是像素。
投影原理
魔卡托投影思路:用一个平面包围成圆柱体,正好与地球相接,地球近似成正球体处理。从球内打射线,跟球面和圆柱面都有唯一的交点。如下图,从球内放置灯光,光线向外,跟球面交点为P,与外接圆柱面的交点为P1,P的经纬度分别为λ,φ。
按照一般四维,投影后的P1和P的经纬度关系是:
投影后的x值正好是弧长(最终投影后的正方形是由圆柱展开得到的,x轴正好是圆柱的圆周面上,所以投影后点的x值正好是弧长)。但是y值正比于tan值,当纬度φ趋向于两极,无限接近正负90°时,tan增长速度非常快,tan函数导数变化很大。最终结果是两极附近的距离被无限放大。
反畸变处理
魔卡托投影最最精妙地地方是y值的处理:用一个奇妙的函数替换了常规的tan函数。
替换后结果为
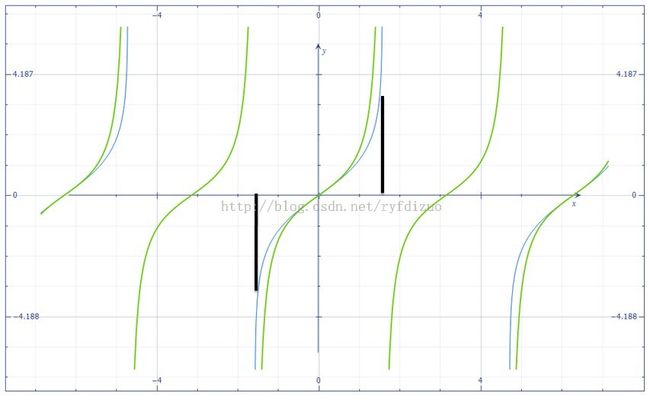
F(Φ) = ln[ tan(π/4 +Φ/2 ) ] 与T(Φ) = tan(Φ)的函数曲线如下:
绿色为T函数,蓝色为F函数,对比发现,当原点附近F函数与y=x函数曲线非常接近,当Φ无限趋近正负π/2时候,tan函数已经趋于无穷,而F函数值仍然处于设定值范围内。F函数趋向无穷的条件值被推迟。
Φ的取值范围为-π/2,π/2,即[-1.57,1.57],地球经纬度近似-85,85,所以最终Φ的取值为-1.5,1.5,即上图中黑色粗线指向的区间。此时F函数值正好位于-π,π。
通过F函数,处理后的纬度值跟经度值范围一致。
从上图可以看出F(Φ) = ln( tan(π/4 + Φ/2) ) 也是关于原点对称的,F(Φ) = -F(-Φ)。通过三角函数可以证明。
参考资料
百度百科:http://baike.baidu.com/view/301981.htm
WIKI:http://en.wikipedia.org/wiki/Scale_(map)