HDU 4285 circuits 解题报告(插头DP)
circuits
Time Limit: 30000/15000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 622 Accepted Submission(s): 185
Problem Description
Given a map of N * M (2 <= N, M <= 12) , '.' means empty, '*' means walls. You need to build K circuits and no circuits could be nested in another. A circuit is a route connecting adjacent cells in a cell sequence, and also connect the first cell and the last cell. Each cell should be exactly in one circuit. How many ways do we have?
Input
The first line of input has an integer T, number of cases.
For each case:
The first line has three integers N M K, as described above.
Then the following N lines each has M characters, ‘.’ or ‘*’.
For each case:
The first line has three integers N M K, as described above.
Then the following N lines each has M characters, ‘.’ or ‘*’.
Output
For each case output one lines.
Each line is the answer % 1000000007 to the case.
Each line is the answer % 1000000007 to the case.
Sample Input
2 4 4 1 **.. .... .... .... 4 4 1 .... .... .... ....
Sample Output
2 6
解题报告:调试了N久的一道题。
最后的做法是将环数看成另外一维= =。
对于环嵌套的判定使用的仍然是网上大家说的,判断一下当前格左边的插头数量,是偶数就可以,奇数就放弃此状态。
奇数肯定会嵌套大家都能理解,偶数为什么就不会嵌套了,一直没搞懂。现在写博客时却忽然明了了。
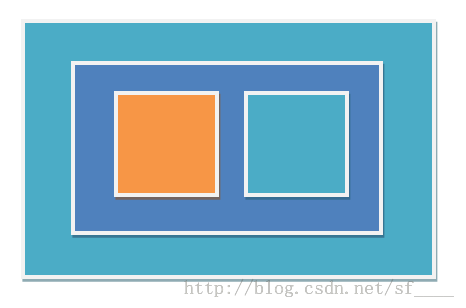
如下图:
黄色的环如果想成环,是可以的,因为左边的插头数为2,偶数。而蓝色的却肯定不能成环,因为它左边的插头数是奇数。蓝色为了不成环,导致外面绿色的也不能成环,他们会相连。
换句话说,嵌套环中,大环内部的小环的插头数一定是奇数。如果所有的环外面都是偶数个插头,就一定不会嵌套。
代码如下,2500MS多。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=29989;
const int MOD=1000000007;
const int L=2;
int now,pre;
int n,m,K,t;
int maze[14][14];
struct Node
{
int H[maxn];
int S[maxn];
int N[maxn];
int size;
void init()
{
size=0;
memset(H,-1,sizeof(H));
}
void push(int SS,int num)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS)
s=(s+1)%maxn;
if( ~H[s] )
{
N[H[s]]+=num;
if(N[H[s]]>=MOD) N[H[s]]-=MOD;
}
else
{
S[size]=SS;
N[size]=num;
H[s]=size++;
}
}
int get(int SS)
{
int s=SS%maxn;
while( ~H[s] && S[H[s]]!=SS)
s=(s+1)%maxn;
if( ~H[s] )
return N[H[s]];
return 0;
}
} dp[2][37];
int get(int S,int p)
{
return (S>>(p*L))&((1<<L)-1);
}
void set(int&S,int p,int v)
{
S^=get(S,p)<<(p*L);
S^=v<<(p*L);
}
void init()
{
t=0;
scanf("%d%d%d",&n,&m,&K);
memset(maze,0,sizeof(maze));
for(int i=0;i<n;i++)
{
char str[100];
scanf("%s",str);
for(int j=0;j<m;j++)
{
if(str[j]=='.')
maze[i][j]=1,t++;
}
}
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
init();
int now=1;
int pre=0;
for(int i=0;i<=K;i++)
dp[now][i].init();
dp[now][0].push(0,1);
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
swap(now,pre);
for(int k=0;k<=K;k++)
dp[now][k].init();
for(int k=0;k<=K;k++)
{
for(int s=0;s<dp[pre][k].size;s++)
{
int S=dp[pre][k].S[s];
int N=dp[pre][k].N[s];
int p=get(S,j);
int q=get(S,j+1);
if(maze[i][j]==0)
{
if(p==0 && q==0)
dp[now][k].push(S,N);
continue;
}
if(p==0 && q==0)
{
if(maze[i][j+1] && maze[i+1][j])
{
set(S,j,1);
set(S,j+1,2);
dp[now][k].push(S,N);
}
}
else if((p>0)^(q>0))
{
if(maze[i+(p>0)][j+(q>0)])
dp[now][k].push(S,N);
set(S,j,q);
set(S,j+1,p);
if(maze[i+(q>0)][j+(p>0)])
dp[now][k].push(S,N);
}
else if(p==2 && q==1)
{
set(S,j,0);
set(S,j+1,0);
dp[now][k].push(S,N);
}
else if(p==1 && q==1)
{
int find=1;
for(int l=j+2;l<=m;l++)
{
int v=get(S,l);
if(v==1) find++;
if(v==2) find--;
if(find==0)
{
set(S,j,0);
set(S,j+1,0);
set(S,l,1);
dp[now][k].push(S,N);
break;
}
}
}
else if(p==2 && q==2)
{
int find=1;
for(int l=j-1;l>=0;l--)
{
int v=get(S,l);
if(v==2) find++;
if(v==1) find--;
if(find==0)
{
set(S,j,0);
set(S,j+1,0);
set(S,l,2);
dp[now][k].push(S,N);
break;
}
}
}
else if(p==1 && q==2)
{
if(k>=K) continue;
int find=0;
for(int l=j-1;l>=0;l--) if(get(S,l)>0)
find++;
if(find%2==0)
{
set(S,j,0);
set(S,j+1,0);
dp[now][k+1].push(S,N);
}
}
}
}
}
for(int k=0;k<=K;k++)
for(int s=0;s<dp[now][k].size;s++)
dp[now][k].S[s]<<=L;
}
printf("%d\n",dp[now][K].get(0));
}
}
最小表示法:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int maxn=29989;
const int mod=1000000007;
const int L=3;
int now,pre;
int maze[15][15];
int code[15],ch[15];
int n,m,K;
struct Node
{
int h[maxn];
LL s[maxn];
int n[maxn];
int size;
void init()
{
memset(h,-1,sizeof(h));
size=0;
}
void push(LL ss,int num)
{
int i=ss%maxn;
for(;~h[i] && s[h[i]]!=ss;i++,i=(i>=maxn?i-maxn:i));
if( ~h[i] )
{
n[h[i]]+=num;
if(n[h[i]]>=mod) n[h[i]]-=mod;
}
else
{
s[size]=ss;
n[size]=num;
h[i]=size++;
}
}
int get(LL ss)
{
int i=ss%maxn;
for(;~h[i] && s[h[i]]!=ss;i++,i=(i>=mod?i-mod:i));
if( ~h[i] )
return n[h[i]];
return 0;
}
} dp[2][37];
void decode(LL s)
{
for(int i=0;i<=m;i++)
code[i]=s&((1<<L)-1),s>>=L;
}
LL encode()
{
memset(ch,-1,sizeof(ch));
ch[0]=0;
int cnt=1;
LL s=0;
for(int i=m;i>=0;i--)
{
if(ch[code[i]]==-1)
ch[code[i]]=cnt++;
code[i]=ch[code[i]];
s<<=L;
s|=code[i];
}
return s;
}
void shift()
{
for(int k=0;k<=K;k++) for(int s=0;s<dp[now][k].size;s++)
dp[now][k].s[s]<<=L;
}
void merge(int a,int b)
{
for(int i=0;i<=m;i++) if(code[i]==a)
code[i]=b;
}
void dpGrid(int i,int j)
{
for(int k=0;k<=K;k++) for(int s=0;s<dp[pre][k].size;s++)
{
decode(dp[pre][k].s[s]);
int num=dp[pre][k].n[s];
int left=code[j];
int up=code[j+1];
int ma=max(left,up);
int mi=min(left,up);
if(maze[i][j]==0)
{
if(ma==0)
dp[now][k].push(encode(),num);
continue;
}
if(ma==0)
{
if(maze[i][j+1] && maze[i+1][j])
{
code[j]=code[j+1]=13;
dp[now][k].push(encode(),num);
}
}
else if(mi==0)
{
if(maze[i+1][j])
{
code[j]=ma;
code[j+1]=0;
dp[now][k].push(encode(),num);
}
if(maze[i][j+1])
{
code[j]=0;
code[j+1]=ma;
dp[now][k].push(encode(),num);
}
}
else if(left==up)
{
code[j]=code[j+1]=0;
if(k<K)
{
int v=0;
for(int c=0;c<j;c++)
if(code[c]>0) v++;
if(v%2==0) dp[now][k+1].push(encode(),num);
}
}
else
{
code[j]=code[j+1]=0;
merge(left,up);
dp[now][k].push(encode(),num);
}
}
}
void solve()
{
now=1,pre=0;
for(int k=0;k<=K;k++) dp[now][k].init();
dp[now][0].push(0,1);
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
swap(now,pre);
for(int k=0;k<=K;k++) dp[now][k].init();
dpGrid(i,j);
}
shift();
}
}
void init()
{
scanf("%d%d%d",&n,&m,&K);
memset(maze,0,sizeof(maze));
for(int i=0;i<n;i++)
{
char str[20];
scanf("%s",str);
for(int j=0;j<m;j++)
if(str[j]=='.')
maze[i][j]=1;
}
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
init();
if(K>m*n/4) {puts("0");continue;}
solve();
printf("%d\n",dp[now][K].get(0));
}
}