投影矩阵与最小二乘（一）

投影矩阵与最小二乘二者有什么必然的联系么，当我开始写这篇文章的时候我也这样问自己。如果Strang教授没有教授这堂课亦或者讲的这堂课没有被放到网上被别人所下载观看，那么...

好在一切都是那么的幸运

先说说投影吧，这个想必大家都知道，高中的知识了。一个向量(b)在另一个向量(a)上的投影：

实际上就是寻找在a上离b最近的点。如果我们把p看作是a的估计值，那么我们定义e = b - p，称e为误差(error)。

现在，我们的任务是找到这样的p，我们可以规定p = xa（x是某个数），那么e = b - xa，因为e与p也就是a垂直，所以有aT(b - xa) = 0，展开化简得到：

将x代入到p中，得到：

我们发现，如果改变b，那么p相对应改变，然而改变a，p无变化。

有了上面的背景知识，我们可以正式进入主题了，投影矩阵(projection matrix)：

p = Pb，

显然这里有：

这里我们最需要关注的是投影矩阵的两个性质：

1）P' = P;

2）P ^ 2 = P;

对于第一个，很容易理解，因为P本身就是个对称阵。第二个，直观的理解就是投影到a上后再投影一次，显然投影并没有改变，也就是二次投影还是其本身。

这个投影到底有什么用呢，从线性代数的角度来说，Ax = b并不一定总有解，这在实际情况中会经常遇到（m > n）。所以我们就把b投影到向量p上，求解Ax = p。

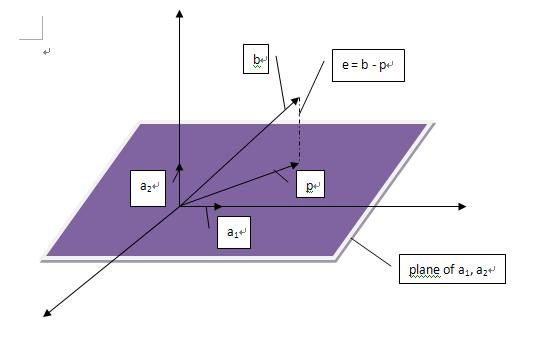
接下来，我们可以考虑更高维度的投影，三维空间的投影是怎么样的呢，我们可以想象一个三维空间内的向量在该空间内的一个平面上的投影：

我们假设这个平面的基(basis)是a1, a2.那么矩阵A = [a1 a2]的列空间就是该平面。假设一个不在该平面上的向量b在该平面上的投影是p，那么我们就有下面这个表达式 p = x1a1 + x2a2 = Ax， 我们的任务就是找到这样的x。这里有一个关键的地方：e = b - Ax与该平面垂直，所以a1'(b - Ax) = 0且a2' (b- Ax) = 0.用矩阵的形式表达就是：

A'(b - Ax) = 0.

从上面这个式子我们可以得到e(e = b - Ax)等于N(A')。回忆之前的四个空间的关系：假设矩阵(m * n)的秩为r，行空间（维度r）与零空间（维度n - r）互相垂直，列空间(维度r)与左零空间(维度为m - r)互相垂直。所以，我们可以得到e垂直于C(A)。

我们把上边式子展开，得到A'Ax = A'b => x = (A'A)-1A'b， p = Ax = A(A'A)-1A'。类似在二维情况下，在三维情况下我们依然有：

1）p' = p;

2）p ^ 2 = p。

好了，在此我们先暂别“投影”。下面，开始说一下最小二乘的故事吧：

在实际应用中，线性回归是经常用到的，我们可以在一张散列点图中作一条直线（暂时用直线）来近似表述这些散列点的关系。比如：

给定二维平面的三个点：(1, 1), (2, 2), (3, 2)。我们想寻求一条直线(y = C + Dt)来逼近这些点。假设这些点都在该直线上，我们有：

C + D = 1

C + 2D = 2

C + 3D = 2.写成矩阵的形式如下：

实际上，这条直线是不存在的。从线性代数的角度来看，就是A的列向量的线性组合无法充满整个列空间，而b恰恰就是一个例外。所以，我们就借助了投影矩阵，我们这么干：

A'Ax = A'b。