hdu 4359 codeforces 9D 组合 二叉树 DP
感觉hdu 4359 跟 codeforces 9D就是差不多的题啊,
比赛时没能回想起来以前是怎么做的,赛后赶紧补习
codeforces 9D ,要求当前点左子树的所有点权都小于当前点的点权,当前点的点权小于右子树的所有点权,问你n个点深度>=h的树共有多少种不同的形状
如样例
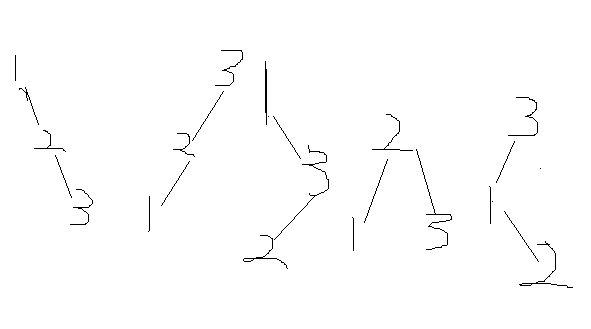
3个点 深度大于等于2
如下图
套用一下codeforces的题解
Denote by tnh the number of binary search trees on n nodes with height equal to h. We will derive a recurrent formula for tnh. For the base case note that t00 = 1 (empty tree), and ti0 = t0i = 0 if i>0.
Now take any binary search tree on n nodes with height equal to h. Let m be the number written at its root, 1 ≤ m ≤ n. The left subtree is a binary search tree on m-1 nodes, and the right subtree is a binary search tree on n-m nodes. The maximal of their heights must be equal to h-1. Consider 2 subcases:
1. The height of the left subtree is equal to h-1. There are tm - 1, h - 1 such trees. The right subtree can have any height from 0 to h-1, so there are such trees. Since we can choose left and right subtrees independently, we have variants in this case.
2. The height of the left subtree is less than h-1. There are such trees, and the right subtree must have height exactly h-1, which gives us totally variants.
So the recurrent formula is the following: .
All the values tnh can be calculated by dynamic programming. The answer, then, is .
很好懂,但是也有另一中方法
dp[i][j]表示i个点组成高度小于等于j的树的总数,写法也自然略微简单了
my code
#include<cstdio>
#include<cstring>
typedef __int64 lld;
lld dp[36][36];
int main()
{
for(int i=0;i<=35;i++) dp[0][i]=1;
for(int i=1;i<=35;i++)
{
for(int j=1;j<=35;j++)
{
for(int k=0;k<i;k++)
{
dp[i][j]+=dp[k][j-1]*dp[i-k-1][j-1];
//printf("i=%d j=%d %I64d\n",i,j,dp[j][j]);
}
}
}
int n,h;
scanf("%d%d",&n,&h);
printf("%I64d\n",dp[n][35]-dp[n][h-1]);
return 0;
}
hdu 4359
注意到当前的根节点可以随便取,因为题目只要求左子树的和小于右子树,那么只要左子树的最大值小于右子树的最大值即可,因为2^0+2^1+2^p-1<2^p。
所以在求dp[i][j]的时候,
1:要么子树的中n-1个点权在左子树,要么全在右子树,因为这样的话就没用条件限制
了
2:如果左右子树都有,那么最大的肯定要放在右子树上,所以除了当前根和最大的点,其他点(总共i-2个)随便取 ,枚举左子树最多放几个,右子树最多放几个就知道了
转移为:
dp[i][j]+=C[i-2][k]*dp[k][j-1]*dp[i-1-k][j-1];这样子做比标称简单不少(代码目前hdu最短),但尤其要注意初始化的细节
dp[i][j]:i个点深度小于等于j时总的树的数量
#include<cstdio>
#include<cstring>
const int mod = 1000000007;
typedef __int64 lld;
const int N = 360;
lld dp[361][361];
lld C[361][361];
int main(){
C[0][0]=1;
for(int i=1;i<=N;i++){
C[i][0]=C[i][i]=1;
for(int j=1;j<i;j++)
C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
}
memset(dp,0,sizeof(dp));
for(int i=0;i<=N;i++) dp[0][i]=1;
for(int i=1;i<=N;i++) dp[1][i]=1;
for(int i=2;i<=N;i++){
for(int j=1;j<=N;j++){
dp[i][j]+=dp[i-1][j-1]*2%mod;
dp[i][j]%=mod;
for(int k=1;k<=i-2;k++){
dp[i][j]+=(C[i-2][k]*dp[k][j-1])%mod*dp[i-1-k][j-1]%mod;
dp[i][j]%=mod;
}
dp[i][j]*=i;
dp[i][j]%=mod;
}
}
int n,h,t,ca=1;
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&h);
printf("Case #%d: %I64d\n",ca++,((dp[n][h]-dp[n][h-1])%mod+mod)%mod);
}
return 0;
}