matlab实现k-means聚类

聚类算法，不是分类算法。

分类算法是给一个数据，然后判断这个数据属于已分好的类中的具体哪一类。

聚类算法是给一大堆原始数据，然后通过算法将其中具有相似特征的数据聚为一类。

这里的k-means聚类，是事先给出原始数据所含的类数，然后将含有相似特征的数据聚为一个类中。

所有资料中还是Andrew Ng介绍的明白。

首先给出原始数据{x1,x2,...,xn}，这些数据没有被标记的。

初始化k个随机数据u1,u2,...,uk。这些xn和uk都是向量。

根据下面两个公式迭代就能求出最终所有的u,这些u就是最终所有类的中心位置。

公式一：

意思就是求出所有数据和初始化的随机数据的距离，然后找出距离每个初始数据最近的数据。

公式二：

意思就是求出所有和这个初始数据最近原始数据的距离的均值。

然后不断迭代两个公式，直到所有的u都不怎么变化了，就算完成了。

先看看一些结果：

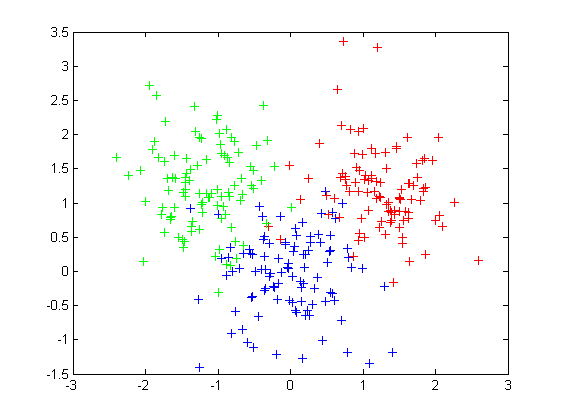
用三个二维高斯分布数据画出的图：

通过对没有标记的原始数据进行kmeans聚类得到的分类，十字是最终迭代位置：

下面是Matlab代码，这里我把测试数据改为了三维了，函数是可以处理各种维度的。

clear all;
close all;
clc;

%第一类数据
mu1=[0 0 0];  %均值
S1=[0.3 0 0;0 0.35 0;0 0 0.3];  %协方差
data1=mvnrnd(mu1,S1,100);   %产生高斯分布数据

%%第二类数据
mu2=[1.25 1.25 1.25];
S2=[0.3 0 0;0 0.35 0;0 0 0.3];
data2=mvnrnd(mu2,S2,100);

%第三个类数据
mu3=[-1.25 1.25 -1.25];
S3=[0.3 0 0;0 0.35 0;0 0 0.3];
data3=mvnrnd(mu3,S3,100);

%显示数据
plot3(data1(:,1),data1(:,2),data1(:,3),'+');
hold on;
plot3(data2(:,1),data2(:,2),data2(:,3),'r+');
plot3(data3(:,1),data3(:,2),data3(:,3),'g+');
grid on;

%三类数据合成一个不带标号的数据类
data=[data1;data2;data3];   %这里的data是不带标号的

%k-means聚类
[u re]=KMeans(data,3);  %最后产生带标号的数据，标号在所有数据的最后，意思就是数据再加一维度
[m n]=size(re);

%最后显示聚类后的数据
figure;
hold on;
for i=1:m 
    if re(i,4)==1   
         plot3(re(i,1),re(i,2),re(i,3),'ro'); 
    elseif re(i,4)==2
         plot3(re(i,1),re(i,2),re(i,3),'go'); 
    else 
         plot3(re(i,1),re(i,2),re(i,3),'bo'); 
    end
end
grid on;

KMeans.m

%N是数据一共分多少类
%data是输入的不带分类标号的数据
%u是每一类的中心
%re是返回的带分类标号的数据
function [u re]=KMeans(data,N)   
    [m n]=size(data);   %m是数据个数，n是数据维数
    ma=zeros(n);        %每一维最大的数
    mi=zeros(n);        %每一维最小的数
    u=zeros(N,n);       %随机初始化，最终迭代到每一类的中心位置
    for i=1:n
       ma(i)=max(data(:,i));    %每一维最大的数
       mi(i)=min(data(:,i));    %每一维最小的数
       for j=1:N
            u(j,i)=ma(i)+(mi(i)-ma(i))*rand();  %随机初始化，不过还是在每一维[min max]中初始化好些
       end      
    end
   
    while 1
        pre_u=u;            %上一次求得的中心位置
        for i=1:N
            tmp{i}=[];      % 公式一中的x(i)-uj,为公式一实现做准备
            for j=1:m
                tmp{i}=[tmp{i};data(j,:)-u(i,:)];
            end
        end
        
        quan=zeros(m,N);
        for i=1:m        %公式一的实现
            c=[];
            for j=1:N
                c=[c norm(tmp{j}(i,:))];
            end
            [junk index]=min(c);
            quan(i,index)=norm(tmp{index}(i,:));           
        end
        
        for i=1:N            %公式二的实现
           for j=1:n
                u(i,j)=sum(quan(:,i).*data(:,j))/sum(quan(:,i));
           end           
        end
        
        if norm(pre_u-u)<0.1  %不断迭代直到位置不再变化
            break;
        end
    end
    
    re=[];
    for i=1:m
        tmp=[];
        for j=1:N
            tmp=[tmp norm(data(i,:)-u(j,:))];
        end
        [junk index]=min(tmp);
        re=[re;data(i,:) index];
    end
    
end

转自：http://www.cnblogs.com/tiandsp/archive/2013/04/24/3040883.html