动态规划 (Dynamic Programming) 之 矩阵链乘法(Matrix Chain Multiplication)

这个问题是动态规划的基础的问题，也是算法导论中讨论过的问题。在这里先简单描述一下。假定有一组矩阵需要做乘法操作。但是我们知道首先矩阵乘法满足了结合律。所以可以按照不同的顺序做乘法。而且不同顺序做乘法最后的乘法次数是不同的。比如〈A₁, A₂, A₃〉分别是10 × 100, 100 × 5, 和 5 × 50。如果按照((A₁ A₂) A₃)的顺序来计算,就是7500次，但是如果(A₁ (A₂ A₃))这样的顺序，那结果就是75000次！！！这里有10倍的差距。所以这个题目的意思就是找到一个方案使得需要做乘法的次数最少。

现在我们尝试用大白话来继续一下。问题的解决方案侧重在两个方面。一个是最少乘法的次数，另一个就是最小乘法次数的流程。在代码中我们分别用m,s来表示。先说一下m的含义。m是个二维数组，m[i,j]表示从矩阵i到矩阵j的最小乘法次数。也就是A[i],A[i+1]....A[j]的最小乘法次数。可以发现，这个次数应该等于A[i],A[i+1]...A[k] * A[k+1]....A[j-1]A[j]的次数，这里的k是输入i到j这个开区间的某个数。找到这个数字，我们也就找到了最小乘法次数。

那怎么找到这个数字呢？简单的说就是把所有的可能性都列举出一遍k=i, i+1, i+2...j都尝试一遍。比较最小值就可以了。有了这个思路我们可以把递归公式写成:

这里的p就是你的矩阵维数的数组。

根据这个公式，我们可以写出下面的代码：

 

#include "stdafx.h" #include <vector> #include <limits> #include <iostream> typedef std::vector< std::vector<int> > intMatrix; /** * Description: Calulate the matrix chain multiplication order *@param p, order of the matrix demension; *@param m, output value, Save the number of the multiplication for specific i,j. * for instance, the number for n matrix will be stored in m[0][n-1]. *@param s, output value, Save the order of multiplication * for instance, s[i,j]=k, means matrix need to multiple in order m[i...k]*m[k+1....j]; *@return number of the multiplication times. */ int matrixChainOrder (const std::vector<int>& p, std::vector < std::vector<int> >& m, std::vector < std::vector<int> >&s) { int n = (int)p.size()-1; m.resize(n); for (int i=0;i<n;i++) m[i].resize(n); s.resize(n); for (int i=0;i<n;i++) s[i].resize(n); for (int l=2;l<=n;l++) { // length of the chain is l for (int i=0;i<n-l+1;i++) { int j=i+l-1; m[i][j] = std::numeric_limits<int>::max(); for (int k=i;k<j;k++) { int q=m[i][k]+m[k+1][j]+p[i]*p[k+1]*p[j+1]; if(q<m[i][j]) { m[i][j]=q; s[i][j]=k; } } } } return m[0][n-1]; } void printSequence(const intMatrix& s, int i, int j) { if (i<j) { std::cout<<"("; printSequence(s, i, s[i][j]); printSequence(s, s[i][j]+1,j); std::cout<<")"; } else std::cout<< "M["<<i<<"]"; } int _tmain(int argc, _TCHAR* argv[]) { int k[]={30,35,15,5,10,20,25}; std::vector<int> p(k,k+sizeof(k)/sizeof(k[0])); intMatrix m; intMatrix s; // number of multiplication std::cout<<"Minimum multiplication times is "<<matrixChainOrder(p, m, s)<<std::endl; // backtrack the sequence printSequence(s, 0,(int)p.size()-2); getchar(); return 0; }

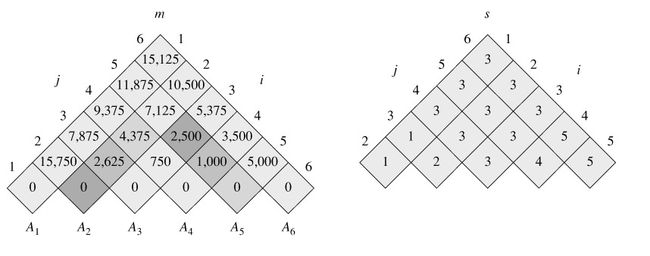
需要注意的问题是，这个算法的复杂度在O(n∧3)。而且这个算法和算法导论等地方的伪码比有些细微的差异体现在数组从0开始还是1开始上。大体上还是一致的。这里的空间复杂度也到了O(n∧2)。大致的计算顺序就是通过这个函数中的l来控制。l=2的时候，依次计算矩阵A[0]*A[1], A[1]*A[2], A[2]*A[3]...的次数。l=3的时候就开始计算A[0]*A[1]*A[2], A[1]*A[2]*A[3]..的次数。用更形象的话来说就是倒三角的顺序。下面的这个图就是对上面流程的描述：

 

最后说一句，这个矩阵链问题是相对独立的一个问题，和其他的知名的问题都没有太大的关联。以后的总结可能有很多不同的变形。