全排序vs八皇后问题vs三角八皇后
假设要求字符串/数组的全排序,例如:"123"的全排序,第1位有3种选择,第2位有2种选择,第3位1种选择,时间复杂度显然是3!.实际上容易知道,对于n个字符,全排序一共有n!种可能,是n!时间复杂度的.我们需要找一个算法求出所有的可能的排序,最好的办法是递归,如果选用循环,需要n层嵌套,不太现实.假设我们已经拥有一个函数 FullPermutation(A[n])能将数组A[n]全排序,于是,我们可以将A[n]分为A[1]和A[n-1]两个子问题,其中,A[1]可以有n种选择,选择办法是:将A[1]和A[i]交换,其中,i=1,2,3,4.......记得交换后,需要复原.A[n-1]的全排序可以通过调用FullPermutation()完成.
递推公式:
F(n): = Done n=1
= n*F(n-1) n>1
一看到这道题,自然反应就是这道题:http://acm.hdu.edu.cn/showproblem.php?pid=1030,这一道题的思路是三维坐标绝对值之和.但是,上面的这一道题是经典的算法实现简单得难以置信,但是原理却是博大精深型的.
递推公式:
F(n): = Done n=1
= n*F(n-1) n>1
由上面的分析和递推公式就很容易写出代码了:
#include<iostream>
using namespace std;
void Full_permutation(int* A,int beg,int end)
{
if(beg == end)
{
for(int i=0;i<=end;++i)
cout<<A[i]<<' ';
cout<<endl;
return ;
}
for(int i=beg;i <= end; ++i)//A[1]有n种选择,需要n次循环
{
swap(A[beg],A[i]); //选择beg的值
Full_permutation(A,beg+1,end);//求解n-1子问题
swap(A[beg],A[i]);
}
}
int main()
{
int A[8]={0,1,2,3,4,5,6,7};
Full_permutation(A,0,7);
return 0;
}
扩展:由时间复杂度为(n!),我们容易联想到n皇后问题,最经典的八皇后问题:在8×8的国际象棋上摆放八个皇后,使其不能相互攻击,即任意两个皇后不得处在同一行、同一列或者同一对角斜线上。我们可以这么分析,先从行入手,第1个皇后可以在第1行上选择8个位置,第2个皇后可以在第2行选择7个位置(只要不和第1个皇后同列),第3个皇后可以在第1行上选择6个位置(只要不和第1,2个皇后同列).如果不考虑对角线的攻击方向,那么n皇后问题可以有n!个解,和上面的全排列一样.同样,我们可以先考虑行和列的n!种所有情况,然后排除对角线冲突的情况,进而缩小范围,就可以找出8皇后的解.基于这个想法,八皇后问题并不难.现在,我们还剩下最后一个问题?用什么数据结构保存皇后的二维坐标,其实很容易,用(i,A[i])就可以保存皇后的位置,即一个数组,索引i表示行,A[i]表示列.定义一个A[8]就可以表示八皇后.由这个思路,代码:
#include<iostream>
using namespace std;
bool isLegalQueens(int* A,int end)
{
for(int i=0; i<=end; ++i)
{
for(int j=i+1; j <=end; ++j)
{
if( A[j]-A[i] == j-i || A[j]-A[i] == i-j )//两点的斜率如果为1或-1,则为不合法
return false;
}
}
return true;
}
void Full_permutation(int* A,int beg,int end)
{
if(beg == end)
{
if(isLegalQueens(A,end))
{
for(int i=0;i<=end;++i)
cout<<A[i]<<' ';
cout<<endl;
}
return ;
}
for(int i=beg;i <= end; ++i)//A[1]有n种选择,需要n次循环
{
swap(A[beg],A[i]);//选择beg的值
Full_permutation(A,beg+1,end);//求解n-1子问题
swap(A[beg],A[i]);
}
}
int main()
{
int A[8]={0,1,2,3,4,5,6,7};
Full_permutation(A,0,7);
return 0;
}
实训:http://acm.hdu.edu.cn/showproblem.php?pid=2804
Queens
Problem Description
Everyone knows about the "eight queens problem", but today you will solve a different one.
We are given triangle lattice of side n, as shown in the Figure below. A queen on the lattice can move along a straight line parallel to any of the sides of the triangle. How many queens can be placed on the lattice at most, without any two queens attacking each other?
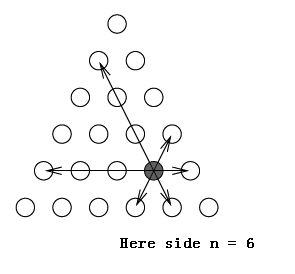
We are given triangle lattice of side n, as shown in the Figure below. A queen on the lattice can move along a straight line parallel to any of the sides of the triangle. How many queens can be placed on the lattice at most, without any two queens attacking each other?

有这么一个结论:
4、一边有 n 个圈的正三角形棋盘,
(1)当 n=3k+1 时,最多可放置(2k+1)个皇后,k=0,1,2,3,……
(2)当 n=3k+2 时,最多可放置(2k+1)个皇后,k=0,1,2,3,……
(3)当 n=3k+3 时,最多可放置(2k+2)个皇后,k=0,1,2,3,……
具体的证明过程见这篇论文:三角形八皇后问题证明
知道上面的结论之后,代码会简洁到难以置信!
#include<iostream>
using namespace std;
typedef long long LLong;
int main()
{
LLong n;
while(cin>>n && n!=0)
{
if( n%3== 0)
cout<<2*(n/3)<<endl;
else
cout<<2*(n/3)+1<<endl;
}
return 0;
}