数学之路(2)-数据分析-R基础(23)

19)分析数据集

接上篇博文~

继续以全球近一周地震数据为例。

我们先将变量放到搜索路径上

> attach(earthquake)

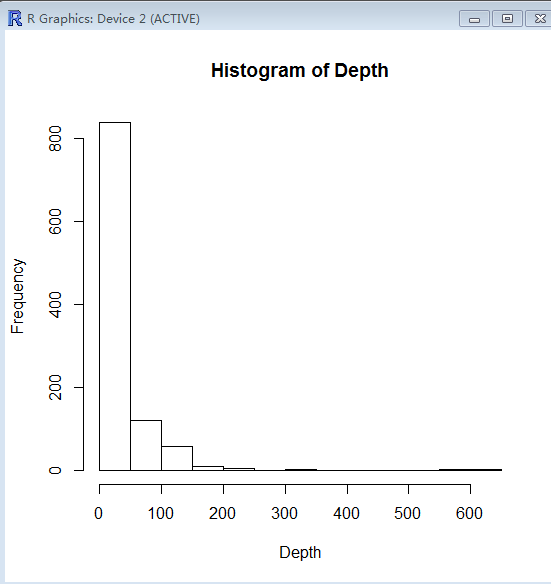
先分析一下地震震深：

> summary(Depth)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 

   0.10    5.80   12.15   30.82   38.00  630.70      39 

Min表示地震震深最小值，Max表示最大值，Median为中位数，Mean为平均值。

我们试着从下面的散点图中观察一下地震震深与震级的关系：

Depth是震深，Magnitude是震级，很有意思的是表面上看过去一周中Depth和Magnitude之间没有关系，仔细观察后这个图，发现一个有趣的结果：当震深超过300后，震级都接近5或在5以上，而在300以内时，震级并不确定。

可以做关于震深的直方图

hist(Depth)

这些只是根据一个星期的数据分析的结果，不一定就代表真正的答案。

lines函数可完成画线

比如说我们绘制一个(10,40)、(20,50)、(30,60)的散点图，并将点连成线

> plot(c(10,20,30),c(40,50,60))

> lines(c(10,20,30),c(40,50,60))

Fivenum函数返回以下数据：minimum, lower-hinge, median, upper-hinge, maximum

> fivenum(Magnitude)

[1] 1.0 1.3 1.7 2.5 6.5

表示震级最小为1.0，最大为6.5，中位数为1.3，通过1.3将一组数据分为上下两组，然后再计算上下两组的中位数1.3与2.5。

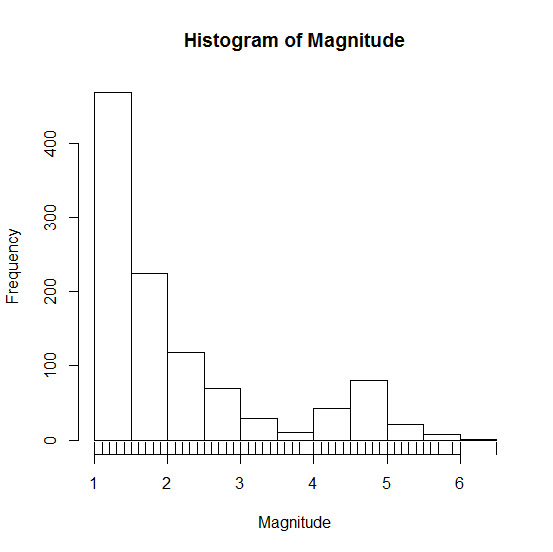
rug函数显示实际的数据点

>  hist(Magnitude)

> rug(Magnitude)

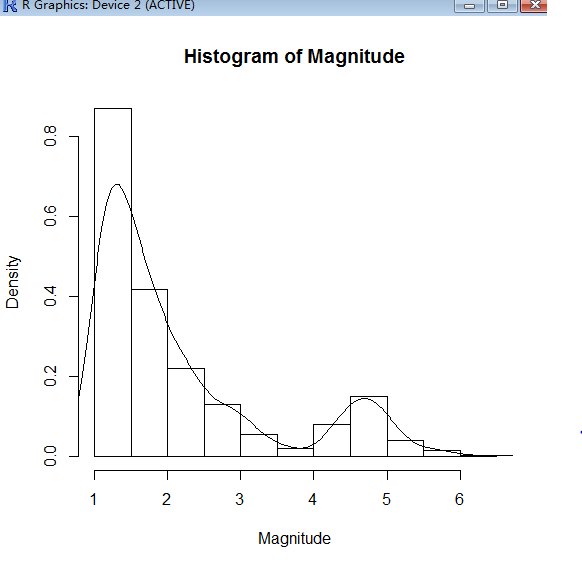
利用直方图估计密度函数存在密度函数是不平滑的，密度函数受子区间宽度影响很大、当数据维数超过2维时有局限性等问题，因此基于核密度估计的方法可解决这些问题。

核密度估计又叫核函数估计(kernel density estimation)，是在概率论中用来估计未知的密度函数，属于非参数检验方法之一，由Rosenblatt (1955)和Emanuel Parzen(1962)提出，又名Parzen窗（Parzen window）。Ruppert和Cline基于数据集密度函数聚类算法提出修订的核密度估计方法。

我们使用density函数进行核密度估计：

> hist(Magnitude,prob=TRUE)

> lines(density(Magnitude))

> 

累积分布函数能完整描述一个实数随机变量X的概率分布，是概率密度函数的积分 ，与概率密度函数相对，定义为随机变量小于或者等于某个数值的概率P（X<=x），即：F(x) = P(X<=x)

Ecdf函数完成累积分布函数的计算，我们计算一下震级的累积分布

> plot(ecdf(Magnitude),do.points=FALSE,verticals=TRUE)

> 

本博客所有内容是原创，未经书面许可，严禁任何形式的转载。

ttp://blog.csdn.net/u010255642