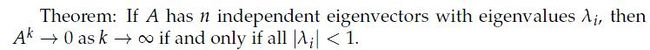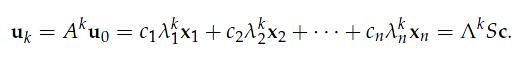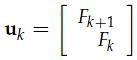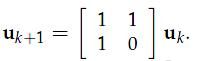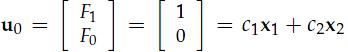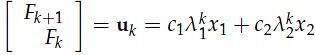解斐波那契数列
斐波那契数列,不多说,这里从0打头:0,1,1,2,3,5,8,13,21,34...
以前解斐波那契数列的通项挺麻烦的,我推过一次,是网上的一个人写的,要构造2次等比数列然后才能得出需要的结果。这里利用线性代数来求解斐波那契数列,整个过程是十分的清新![]()
首先,介绍有关背景知识:
1.特征值,特征向量(eigenvalues, eigenvectors)
2.矩阵对角化
如果一个矩阵A(n by n)有n个线性无关的特征向量(x1, x2, x3 ...),可以把它们以列的形成放在一起形成一个矩阵S,
S = [x1 x2 x3 ... xn];
那么
这里,大写的lambda是一个对角阵,对角元素正是A的n个特征值。由之前S的各列线性无关可知inv(S)存在,所以我们可以得到
3.矩阵的幂
由2我们很容易得到
类似,我们还有
4.定理
如果矩阵A有n个线性无关的特征向量,对应于n个特征值lambda(i)(i = 1 : n),那么当k->无穷大时,A的k次幂趋近于0成立的条件当且仅当所有的lambda(i)的绝对值小于1.
5.差分方程
其中Uk(k = 1 : n)是向量序列(a sequence of vectors),初始状态是U0。
上面这个等式叫做一阶差分方程(first order difference equation)。
它的解具有如下的形式:
我们对此不作证明,只把它当成结论来使用,并且能得到下面更为拉风的式子:
trick: 将U0写成是A的特征向量的线性组合
我们有
利用3,得到
当当当当,主角登场![]()
Fibonacci Sequence
一般来说,有
借用线性代数之手,我们能够探究一些关于斐波那契数列的内幕,比如,该数列的增长速率如何,我为什么要关心这些呢,我现在不知道,鬼才知道。端午节没吃到粽子的我此刻话确实有点多
上面说到了一阶差分,斐波那契数列是二阶差分。但是我们可以使用一些技巧(trick)把它变成一阶差分来对它进行求解。
TRICK:
我们得到了一个很优雅的“一阶差分方程”,由5我们可以知道,只要得到[1 1; 1 0]这个矩阵的特征值,我们就可以解出Uk,也就解出了Fk。求解特征值过程省略,实际上我们可以心算出来![]() 。想必一个是lambda(1) = ( 1 + sqrt( 5 ) ) / 2 ,另一个是lambda(2) = ( 1 - sqrt( 5 ) ) / 2。前者约等于1.618,后者约等于-0.618.
。想必一个是lambda(1) = ( 1 + sqrt( 5 ) ) / 2 ,另一个是lambda(2) = ( 1 - sqrt( 5 ) ) / 2。前者约等于1.618,后者约等于-0.618.
我们得出结论:
斐波那契数列的增长率由较大的特征值(实际上,应该说由绝对值大于1的特征值)控制,即大约是1.618.为什么这么说呢,我们可以这样想:
这里由于lambda(2)的绝对值小于1,那么最右边的部分会逐渐趋近于0。
下面求解Fk:
解得
因为
所以
大功告成![]()