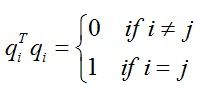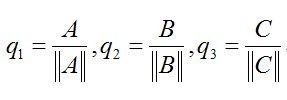正交矩阵和Gram-Schmidt正交化
在关于投影矩阵的部分,根据Strang的授课内容,我进行简单的归纳总结.知道了投影矩阵是什么,有什么用.
这篇文章仍然是关于投影矩阵的一个应用.
什么是正交矩阵和Gram-Schmidt正交化,相信学过线性代数的朋友们都知道.
这里,我只想说标准正交化和标准正交矩阵带来的好处.
标准正交化(orthonormal)的定义是:如果向量q1,q2,...,qn满足下式
则q1,q2,...,qn是标准正交的
我们很容易得出,如果一个矩阵Q的列向量是标准正交的,那么Q'Q=I.如果Q还是个方阵,那么就称矩阵Q是正交矩阵.且有Q'Q=I ==> Q' = Q-1
鉴于正交矩阵这个优良的特性,如果一个向量b投影到Q上,Q是正交阵的话,投影矩阵就变得简单了:
P=Q(Q'Q)-1Q'=QQ'=I,对于最小二乘问题Q'Qx=Q'b,可简化为x=Q'b,即
下面要说下Gram和Schmidt给我们带来的Gram-Schmidt正交化方法,它使得矩阵分析变得简单.
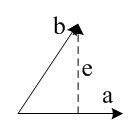
假设在R2空间内的两个相互独立的向量a,b,他们共同生成了R2空间,如下图所示
向量a和b的方向都是任意的,但是二者并不垂直,a的方向不是一定为水平的,这里只是为了好看起见
我现在想找两个向量A,B,他们不仅相互独立,且正交,也就是A和B生成的空间与a和b生成的空间一样,但是A和B是垂直的.
怎么办呢,之前学过的投影矩阵似乎能帮上忙,如下图
图中e是和a垂直的,e=b-xa(如果这个不明白怎么来的,请大家看投影矩阵系列的三篇文章)\
所以,我们取A=a,B = b-xA=b - A'b/(A'A) * A
R3空间中的正交化公式同理可以简单推出:
然后,我们把向量A,B,C normalize一下(Stang说这可能是他所记得的Schmidt对此公式的唯一贡献)
由此,引出了重要的矩阵分解中的QR分解
我们假定A = [a1 a2],那么A可以分解为一个正交阵(Q)和一个上三角阵(R)的乘积
说实话,上面这个式子我到现在也还没弄明白到底是怎么来的,有谁能告诉我吗
等式右边q1,q2,q3与三维数组的第一列相乘得到a,第二列得到b,第三列怎么得到c的呢,我实在没看出来,如果谁看出来,麻烦告诉我下