SIFT特征详细描述
一、介绍
特征的检测和匹配在许多计算机视觉应用中是一个重要的组成部分,例如无缝拼接,三维重建等。其中兴趣点特征是很重要的一类特征,而目前应用最广泛的兴趣点特征检测方法就是SIFT检测算法,该检测算法所得到的特征点不仅在位置上能够稳定识别,而且具有尺度不变性和旋转不变性。由于各大论坛以及该论文作者都只是给出matlab的实现算法,并未给出C++的版本,而且由于在SIFT的实现过程中有很多参数设置和细节上的优化处理,实现起来比较复杂。该程序使用主流的开源的OpenCV库函数给出了C++版本的SIFT特征检测算法,并结合样例,详细地描述了实现过程中的大部分细节。
二、算法描述
SIFT特征不只具有尺度不变性,即使改变旋转角度,图像亮度或拍摄视角,仍然能够得到好的检测效果。由于SIFT算法有很多操作,会令人不解,这里将整个算法分为多个部分:
1. 构建尺度空间
这是一个初始化操作,通过生成尺度空间来创建原始图像的多层表示以保证尺度不变性。
2. LoG近似
使用Laplacian of Gaussian能够很好地找到找到图像中的兴趣点,但是需要大量的计算量,所以使用创建更容易的表示来近似它。
3. 找到关键点
利用很快的近似,我们可以找到特征点,它们是Difference of Gaussian图像的极大极小值。
4. 除去不好的特征点
边界和低亮度区域是不好的特征点,除去它们以使得算法有效和鲁棒,在这里使用近似Harris Corner检测器。
5. 给特征点赋值一个方向
为每个特征点计算一个方向,依照这个方向做进一步的计算,这个操作有效地取消了方向的影响,使得算法具有旋转不变性。
6. 生成SIFT特征
最后,利用位置上的尺度和旋转不变性,能够生成一个表示,它能帮助唯一地识别特征。通过这个表示,我们可以很容易识别寻找的特征。
2.1创建尺度空间
真实世界的物体只在某一尺度下是有意义的。靠近的时候,我们能够看清楚的东西,可能远离的时候就不见了;带上眼镜能够看清楚的东西,可能脱下眼镜就看不见了。物体这种多尺度的性质是很常见的,并且尺度空间就是将这个性质用在数字图像中。
尺度空间
你是想看树叶还是整棵树?如果是树,就要有目的摆脱图像中的细节(像树叶,小枝等),当摆脱了这些细节,还要避免引入新的错误的细节。唯一的方法就是使用高斯模糊(在几个合理的假设下,这是经过数学证明的)。
|
 |
所以为了创建一个尺度空间,我们可以利用原始的图像来逐渐生成模糊后的图像,下图显示了图像是如何摆脱细节的,如猫的胡须。
在SIFT中的尺度空间
1. 组数和尺度数依赖于原始图像的大小,SIFT算法发明者建议将组数设为4,尺度数设为5是比较理想的。在实现中我们采用作者的建议。
SIFT需要多组(octave)尺度空间,用第一幅图像逐渐生成一组模糊后的图像,然后将原始图像的尺寸缩小一半,再逐渐生成下一组模糊后的图像,以此类推。
相同大小的图像形成一组尺度空间,上面有四组尺度空间,每组有5张图像,且这些图像通过增加尺度(模糊量)逐渐形成。
在SIFT算法的第一阶段,我们生成了原始图像的多组尺度空间,每个组的图像大小是前者的一半。在一组尺度空间中,图像使用高斯模糊操作被逐渐模糊。
实现细节
2. 第一组的图像并不是直接使用原始图像,而是使用大小放大两倍并稍微模糊后的图像,这样可以多产生4倍的特征点。
3. 数学上,模糊指的是图像与高斯核的卷积,卷积后的图像是一个模糊的图像。
4.每个图像的模糊量是很重要的,假设一幅图像的模糊量是σ,那么下一幅图像的模糊量是k*σ,这里的k是一个常量。
图2.3 四组尺度空间中每幅图像分别对应的尺度量,这是我们程序中所使用的σ图表,在同一组中,下一幅图像比前一幅图像在σ上相差sqrt(2),即![]() 。
。
2.2 Laplacian of Gaussian的近似
在上一步,我们通过逐渐模糊图像,创建了图像的尺度空间。现在使用这些模糊的图像来生成另一类图像组Differece of Gaussain(DoG),这些DoG图像很适合在图像中找感兴趣的特征点。
Laplacian of Gaussian
Laplacian of Gaussian操作按下面进行,取一张图像将其模糊一点,并且计算它的二阶导数,这样可以定位图像中的边界和直角。这些边界和直角对于找到特征点是很有帮助的。但是二阶导数对噪音是非常敏感的,通过使用模糊操作平滑噪音,可以稳定了二阶导数。这个问题计算所有二阶导数需要大量的计算,所以使用近似操作。
近似的好处
Difference of Gaussian图像近似等于Laplacian of Gaussian,并且我们用一个简单的减法来替换计算量大的Laplacian操作,这些DoG图像是尺度不变的。
只是对图像进行Laplacain操作不够好,得到的图像还不是尺度不变的,因为它们还依赖于模糊量σ。高斯表达式的分母中有σ2项,它就是尺度,只有除去它,才能得到真正的尺度不变性。所以如果将Laplacian of Gaussain表示为![]() ,那么尺度不变的Laplacian of Gaussian就是
,那么尺度不变的Laplacian of Gaussian就是![]() ,但是所有这些都可以通过Difference of Gaussian操作来表示,并且通过证明这样的尺度不变操作可以产生更多可跟踪的特征点。
,但是所有这些都可以通过Difference of Gaussian操作来表示,并且通过证明这样的尺度不变操作可以产生更多可跟踪的特征点。
|
实现细节
这里用一系列图像来说明这些difference of Gaussian是如何实现的,如图2.5所示。
在这一组图像中,对每两幅尺度相邻的图像做减法操作,就可以生成相应的DoG图像。每组图像中两个连续图像被选择,并用一幅图像减去另一幅图像,然后下一对图像也被选择,这个过程重复进行,并用于每一组图像。由于尺度数设为5,每组图像可以得到4幅DoG图像。这个DoG图像是尺度不变的Laplacian of Gaussian,它对于检测特征点是很有用的。
2.3 找到特征点
到现在,我们已经生成了一个尺度空间,并且使用尺度空间来计算Difference of Gaussian,它们被用于计算尺度不变性的Laplacian of Gaussian的近似。通过得到的DoG图像可以找到好的特征点,分为两个子步骤:
1. 在DoG图像中找到极大或极小像素点
2. 找到子像素级的极大极小值点
极大或极小像素点
第一步是粗糙地找到极大极小值像素点,这很简单,我们可以扫描每个像素并且检测所有的邻接像素点,邻接像素点不仅包括当前图像中的邻接像素,而且包括上一层和下一层图像中的邻接像素。
|
X标记当前像素点,绿色的圈标记邻接像素点,用这个方式,最多检测26个像素点。X被标记为特征点,如果它是所有邻接像素点的最大值或最小值点。
通常对于非极大或极小值点不需要遍历所有26个邻接像素点,少数的几个检测就足够抛弃它。注意最高层和最底层的尺度是不需要检测的,经过上一个操作,我们从每组图像中得到4幅DoG图像,只需要对中间的两幅DoG图像进行极大极小值像素点进行检测。
这步结束后,所标记的点就是近似的极大极小值点,之所以说是“近似的”是因为极大极小值点都不会巧好在像素点的位置上,它一般位于像素的中间,但是我们无法直接访问像素间的数据,所以我们需要通过插值得到子像素的位置。如下图所示:
|
红色的叉标记图像中的像素,但是真正的极值点是绿色的位于像素间的点。
子像素的极大或极小像素点
使用可用的像素数据,可以生成子像素的值,它通过近似的特征点附近图像的Taylor展开来计算,数学上的形式如下:
通过对x求偏导并将结果置为零,我们可以简单地计算出方程的极值,从而得到子像素特征点的位置,这些子像素点可以增加匹配和算法稳定性的机率。
若子像素点与近似特征点间的偏移量大于0.5,则按照偏移近似特征点的方向相应改变(移动)特征点,然后再把该点当做近似特征点,重复该操作,直到子像素点与近似特征点间的偏移量小于等于0.5。
实现细节
图2.8给出了经过上面两个子步骤得到的子像素极大极小值点,SIFT算法的作者建议生成两个极值点图像,所以我们只需要4幅DoG图像。为了生成4幅DoG图像,我们需要5幅高斯模糊的图像,因此每组图像需要5层模糊图像。该图中,我们只显示了一组图像,但程序中要对每组图像都这么执行。
|
2.4 消除边界和低对比度的特征
从上一步能产生许多特征点,其中的一些特征点位于边界,或者亮度上没有足够的对比度。在这些情况下,它们都不是有用的特征,所以我们要抛弃它们。我们使用类似于Harris Corner检测中所使用的方法来去除位于边界上的特征,通过检测亮度来去除低对比度的特征。
移除低对比度的特征
如果从DoG图像中检测到的特征点的亮度值少于某个值,那么该特征点就被拒绝。因为我们已经得到子像素的特征点(极大或极小像素点),我们可以得到子像素的亮度,如果亮度少于某个值,那么就拒绝它。
移除边界特征
要想移除边界特征,我们要计算特征点附近高斯模糊图像的梯度。基于特征点附近的图像,有三种可能的特征:
1. 平坦特征
该特征两个方向的梯度值都很小。
2. 边界特征
该特征一个方向的梯度值很大(垂直于边界的方向),另一个方向的梯度值很小(沿着边界的方向)。
3. 直角特征
该特征两个方向的梯度值都很大。
直角特征是很好的特征点,所以我们想得到直角特征,如果特征点的两个方向的梯度值都很大,那么就让它通过,否则就拒绝它。这可以通过Hessian矩阵实现,使用这个矩阵我们可以很容易地检测它是不是直角特征。在SIFT算法中,不需要像Harris corner检测直接计算Hessian矩阵的两个特征值,而只需要计算两个特征值的积与和的比率。
实现细节
下面用例子来说明,如图2.9所示。
|
两个包含特征点的图依次通过这两个测试:对比度测试和边界测试,并去掉未通过测试的特征点。
2.5 分配特征点的方向
在上个步骤,我们得到了合理的特征点,并且这些特征点被测试是在位置上稳定的,容易识别匹配的。由于我们已经知道特征点是在哪个尺度被检测到的,所以这些特征点也是尺度不变的。接下来要对每个特征点赋一个方向,以使这些特征点具有旋转不变性。特征点所拥有的不变性越多越好。
特征点的方向
在每个特征点周围计算图像的梯度方向和大小,我们可以得到最显著的方向,并且将该方向赋给该特征点。后面的操作都相对该方向进行计算,确保了旋转不变性。
|
在特征点附近,我们创建一个方向收集区域来控制该特征点影响的范围,方向收集区域的大小依赖于它所在图像的尺度,尺度越大,收集的区域越大。在方向收集区域中每个像素点的梯度大小和方向用下面的公式计算,从而得到另外两幅图,分别是梯度的大小图和方向图。
我们用一个直方图来统计方向收集区域中像素的平均方向,在该直方图中,将360度的方向分成36个bins,每个bin包含10度。假设方向收集区域中某个像素点的梯度方向是18.75度,把它放入10-19度的bin中,并且加入到bin中的量与该像素点的梯度大小成正比。
一旦对方向收集区域中的每个像素点都执行了这个操作后,直方图在某个bin上出现最高峰值。如图2.11直方图的最高峰值在20-29度,所以特征点的方向被赋值为3(第三个bin)。并且所有大于最高峰80%的峰值也被转化为一个新的特征点,这个新的特征点和原来的特征点一样拥有相同的位置和尺度,但是新特征点的方向是另一个峰值。所以方向将一个特征点分为多个特征点。
|
实现细节
如前面所述,在直方图的统计方向的过程中,需要往相应的bin中加入与当前像素梯度相关的量,这个量应是将图2.10中的梯度大小图进行1.5倍图像尺度量的高斯模糊后的梯度大小值。
方向收集区域的窗口大小等于1.5倍图像尺度量的高斯窗口的大小。
2.6 生成SIFT描述子
这是SIFT算法的最后一步,现在我们已经得到了拥有尺度不变性和旋转不变性的特征点,接下来要为每个特征点创建一个唯一标识它的“指纹”,SIFT算法作者将它称为SIFT描述子(descriptor)。所生成的SIFT描述子既要能让相同场景中图像的特征点能够正确匹配,而且还要让不同场景中图像的特征点能够正确区分。
为了得到这样的SIFT描述子,我们将特征点周围16*16的窗口分解为16个4*4的子窗口,图2.12显示了分解的过程。在每个4*4的子窗口中,计算出梯度的大小和方向,并用一个8个bin的直方图来统计子窗口的平均方向,如图2.13所示。
|
|
梯度方向在0-44度范围的像素点被放到第一个bin中,45-89度范围的像素点被放到下一个bin中,依此类推。同样加入到bin中的量依赖于该像素点梯度的大小。与之前不同的是,加入的量不仅与像素点的梯度大小相关,而且还依赖离特征点的距离,这样远离特征点的像素点会加入较少的量到直方图中。这通过一个高斯加权函数来实现,这个函数生成一个加权值(像一个二维的钟形曲线),用它乘以16*16的窗口中每个像素点的梯度大小,得到加权后的梯度大小,距离特征点越远,要加入直方图的像素点的梯度大小越小。
这样每个4*4的子窗口都对应一个8 bin的直方图,且直方图中加入的值是像素的用高斯加权后的梯度大小,而特征点周围16*16的窗口中包含16个4*4的子窗口,共有16*8=128个数,然后将这128个数组成的向量进行单位化,单位化后的128维向量就是SIFT的描述子。
实现细节
在最后得到SIFT描述子前,我们还要处理两个问题:旋转依赖和亮度依赖。
由于SIFT描述子中包含梯度方向信息,如果我们旋转图像,那么所有的梯度方向都会改变。为了实现旋转不变性,要使用2.5中计算出的特征点方向,在使用每个4*4子窗口中像素的梯度方向时,要先减去特征点方向。
由于某些图像亮度变化较大,这可能会导致特征点周围像素的梯度大小变化过大,也就是说在单位化后的SIFT描述子中某些维度的量要远大于其它维度的量。为了减少亮度的依赖,我们将128维SIFT描述子中大于0.2的维度量截取为0.2,并对最后的128为描述子再做一次单位化。
通过这系列操作,我们最后得到了具有位置稳定、尺度不变性、旋转不变性和较少亮度依赖的SIFT描述子。
三、程序说明
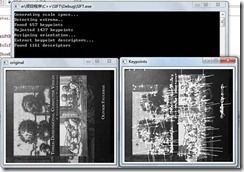
下面是程序的截图,从图中找到了657个具有稳定位置的特征点,为此丢弃了1437个对比度低的特征点或边界特征点。在特征点方向的计算中,将具有稳定位置的特征点进行分离,增加了特征点的数量,产生了1161个的特征点。
左图是原始输入的图像,右图是显示了657个稳定特征点的位置,关联的直线的方向表示最大的梯度方向(未显示其它方向的特征点),直线的长度是10倍的最大梯度大小。