《最优化计算方法》这门课中所有的方法在回归分析的比较与分析

   现在我直接给出实验结果和代码，公式推导在前面几节已经给出，现在给出分析。

  实验结果

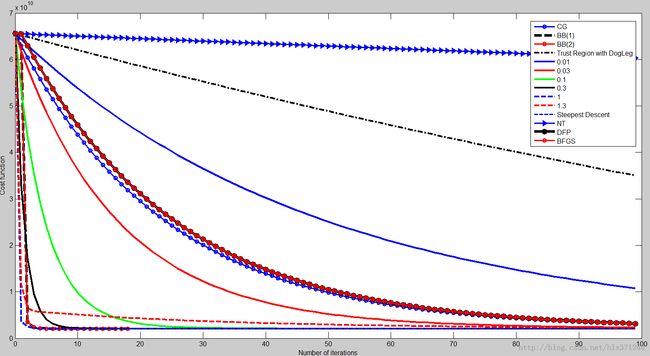
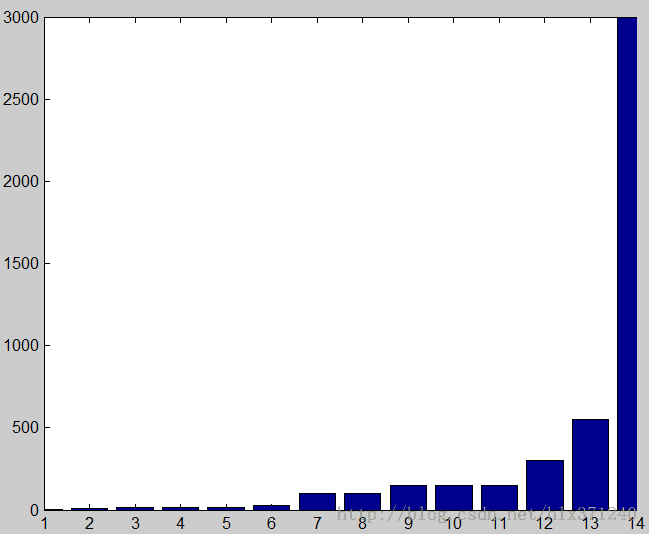
收敛性排名

1-14分别是a=1,BB(1),BB(2),a=0.3,a=0.1,a=1.3,a=0.03,CG,DFP,BFGS,0.01,steepset Descent,Turst Region with DogLeg,Newton(NT).

其中两种拟牛顿法重合，收敛性一样。SD(Steepest Descent)与a=0.03重合。收敛性最好是a=1,最差的是牛顿法。DFP,BFGS,CG下降比较缓慢。

读者可根据收敛性快慢来选取所需要的方法。

后面还会介绍有限内存的BFGS

main.m

x = load('ex3x.dat');        
y = load('ex3y.dat');        
        
trustRegionBound = 1000;        
x = [ones(size(x,1),1) x];        
meanx = mean(x);%求均值        
sigmax = std(x);%求标准偏差        
x(:,2) = (x(:,2)-meanx(2))./sigmax(2);        
x(:,3) = (x(:,3)-meanx(3))./sigmax(3);        
itera_num = 1000; %尝试的迭代次数        
sample_num = size(x,1); %训练样本的次数        
jj=0.00001;    
figure        
alpha = [0.01, 0.03, 0.1, 0.3, 1, 1.3];%因为差不多是选取每个3倍的学习率来测试，所以直接枚举出来    
plotstyle = {'b', 'r', 'g', 'k', 'b--', 'r--'};    
theta_grad_descent = zeros(size(x(1,:)));      
%% CG方法  
theta = zeros(size(x,2),1); %theta的初始值赋值为0          
Jtheta = zeros(itera_num, 1);      
Jtheta(1) = (1/(2*sample_num)).*(x*theta-y)'*(x*theta-y);      
grad1=(1/sample_num).*x'*(x*theta-y);      
Q=x'*x;    
d1=-grad1;    
a1=-(grad1'*d1)/(d1'*Q*d1);    
theta=theta+a1*d1;    
d_old=d1;    
for i = 2:itera_num %计算出某个学习速率alpha下迭代itera_num次数后的参数                 
        Jtheta(i) = (1/(2*sample_num)).*(x*theta-y)'*(x*theta-y);%Jtheta是个行向量      
        g=(1/sample_num).*x'*(x*theta-y);    
        d=-g;    
        beta=(g'*Q*d_old)/(d_old'*Q*d_old);    
        d_new=-g+beta*d_old;    
        a=-(g'*d)/(d'*Q*d);    
        theta=theta+a*d;    
        d_old=d_new;       
end      
plot(0:99, Jtheta(1:100),'b-o','LineWidth', 2);%此处一定要通过char函数来转换       
hold on      
  
  
%% BB(1)+(2)法     
% BB(1)    
theta_old = zeros(size(x,2),1); %theta的初始值赋值为0        
Jtheta = zeros(itera_num, 1);    
%求解a1,d1    
Jtheta(1) = (1/(2*sample_num)).*(x*theta_old-y)'*(x*theta_old-y);    
grad1=(1/sample_num).*x'*(x*theta_old-y);    
Q=x'*x;    
d1=-grad1;    
a1=(grad1'*grad1)/(grad1'*Q*grad1);    
theta_new=theta_old+a1*d1;    
for i = 2:itera_num %计算出某个学习速率alpha下迭代itera_num次数后的参数               
        Jtheta(i) = (1/(2*sample_num)).*(x*theta_new-y)'*(x*theta_new-y);%Jtheta是个行向量    
        grad_old=(1/sample_num).*x'*(x*theta_old-y);    
        grad_new = (1/sample_num).*x'*(x*theta_new-y);    
        if abs(grad_new)<jj    
            M=i;    
            break;    
        end    
        d=-grad_new;      
        s=theta_new-theta_old;    
        g=grad_new-grad_old;    
        a=(s'*g)/(g'*g);      
        theta_old=theta_new;    
        theta_new = theta_old + a*d;      
end    
plot(0:M-1, Jtheta(1:M),'k--','LineWidth', 4)%此处一定要通过char函数来转换     
hold on     
%BB(2)    
theta_old = zeros(size(x,2),1); %theta的初始值赋值为0        
Jtheta = zeros(itera_num, 1);    
%求解a1,d1    
Jtheta(1) = (1/(2*sample_num)).*(x*theta_old-y)'*(x*theta_old-y);    
grad1=(1/sample_num).*x'*(x*theta_old-y);    
Q=x'*x;    
d1=-grad1;    
a1=(grad1'*grad1)/(grad1'*Q*grad1);    
theta_new=theta_old+a1*d1;    
for i = 2:itera_num %计算出某个学习速率alpha下迭代itera_num次数后的参数               
        Jtheta(i) = (1/(2*sample_num)).*(x*theta_new-y)'*(x*theta_new-y);%Jtheta是个行向量    
        grad_old=(1/sample_num).*x'*(x*theta_old-y);    
        grad_new = (1/sample_num).*x'*(x*theta_new-y);    
        if abs(grad_new)<jj    
            M1=i;    
            break;    
        end    
        d=-grad_new;      
        s=theta_new-theta_old;    
        g=grad_new-grad_old;    
        a=(s'*s)/(s'*g);      
        theta_old=theta_new;    
        theta_new = theta_old + a*d;      
end    
plot(0:M1-1, Jtheta(1:M1),'r-o','LineWidth', 2)%此处一定要通过char函数来转换     
hold on     
    
    %% 信赖域+狗腿法      
theta = zeros(size(x,2),1); %theta的初始值赋值为0        
Jtheta = zeros(itera_num, 1);        
 for i = 1:itera_num %计算出某个学习速率alpha下迭代itera_num次数后的参数               
        Jtheta(i) = (1/(2*sample_num)).*(x*theta-y)'*(x*theta-y);%Jtheta是个行向量        
        grad = (1/sample_num).*x'*(x*theta-y);        
        B=x'*x;        
        du = -grad' * grad * grad / (grad' * B * grad);        
        dB = -B^-1 * grad;        
        a = 2;        
        if du'*du > trustRegionBound*trustRegionBound;        
        a = trustRegionBound / sqrt((du'*du));        
        else if dB'*dB > trustRegionBound*trustRegionBound        
        a = sqrt((trustRegionBound*trustRegionBound - du'*du) / ((dB-du)'*(dB-du))) + 1;        
            end            
        end        
        if a < 1        
        d = a * du;        
        else        
        d = du + (a - 1) * (dB - du);        
        end        
        Jtheta1(i)=(1/(2*sample_num)).*(x*(theta+d)-y)'*(x*(theta+d)-y);        
        p = (Jtheta(i)-Jtheta1(i))/(-grad'*d-1/2*d'*B*d);        
            if p > 0.75 && sqrt(abs(d'*d) - trustRegionBound) < 0.001        
        trustRegionBound = min(2 * trustRegionBound, 10000);        
           else if p < 0.25        
            trustRegionBound = sqrt(abs(d'*d)) * 0.25;        
               end        
            end        
         if p > 0%q(zeros(2,1),x) > q(d, x)        
        theta = theta + d;        
         end        
 end        
K(1)=Jtheta(500);        
    plot(0:99, Jtheta(1:100),'k-.','LineWidth', 3)%此处一定要通过char函数来转换        
    hold on        
%% 固定学习率法      
        
theta_grad_descent = zeros(size(x(1,:)));        
for alpha_i = 1:length(alpha) %尝试看哪个学习速率最好        
    theta = zeros(size(x,2),1); %theta的初始值赋值为0        
    Jtheta = zeros(itera_num, 1);        
    for i = 1:itera_num %计算出某个学习速率alpha下迭代itera_num次数后的参数               
        Jtheta(i) = (1/(2*sample_num)).*(x*theta-y)'*(x*theta-y);%Jtheta是个行向量        
        grad = (1/sample_num).*x'*(x*theta-y);        
        theta = theta - alpha(alpha_i).*grad;        
    end        
    K(alpha_i+1)=Jtheta(500);        
    plot(0:99, Jtheta(1:100),char(plotstyle(alpha_i)),'LineWidth', 3)%此处一定要通过char函数来转换        
    hold on        
end    
    
%% SD算法    
theta = zeros(size(x,2),1); %theta的初始值赋值为0        
Jtheta = zeros(itera_num, 1);        
 for i = 1:itera_num %计算出某个学习速率alpha下迭代itera_num次数后的参数               
        Jtheta(i) = (1/(2*sample_num)).*(x*theta-y)'*(x*theta-y);%Jtheta是个行向量        
        grad = (1/sample_num).*x'*(x*theta-y);        
        Q=x'*x;      
        d=-grad;      
        a=(grad'*grad)/(grad'*Q*grad);      
        theta = theta + a*d;         
 end        
K(1)=Jtheta(500)        
    plot(0:99,Jtheta(1:100),'b--','LineWidth', 2);      
    hold on   
%% 牛顿法  
theta = zeros(size(x,2),1); %theta的初始值赋值为0        
Jtheta = zeros(itera_num, 1);  
Q=x'*x;  
for i = 1:itera_num %计算出某个学习速率alpha下迭代itera_num次数后的参数               
        Jtheta(i) = (1/(2*sample_num)).*(x*theta-y)'*(x*theta-y);%Jtheta是个行向量        
        grad = (1/sample_num).*x'*(x*theta-y);            
        d=-(inv(Q)*grad);      
        a=(grad'*grad)/(grad'*Q*grad);      
        theta = theta + a*d;         
 end        
K(1)=Jtheta(500)        
plot(0:99, Jtheta(1:100),'b->','LineWidth', 2);      
hold on   
theta_old = zeros(size(x,2),1); %theta的初始值赋值为0        
Jtheta = zeros(itera_num, 1);  
Jtheta(1) = (1/(2*sample_num)).*(x*theta_old-y)'*(x*theta_old-y);    
grad1 = (1/sample_num).*x'*(x*theta_old-y);  
Q=x'*x;  
a=(grad1'*grad1)/(grad1'*Q*grad1);  
H=inv(Q);  
d1=-(H*grad1);  
theta_new=theta_old+a*d1;  
for i = 2:itera_num %计算出某个学习速率alpha下迭代itera_num次数后的参数               
        Jtheta(i) = (1/(2*sample_num)).*(x*theta_new-y)'*(x*theta_new-y);%Jtheta是个行向量        
        grad_old=(1/sample_num).*x'*(x*theta_old-y);    
        grad_new = (1/sample_num).*x'*(x*theta_new-y);   
        L=grad_new-grad_old;  
        s=theta_new-theta_old;  
        H=H-(H'*L*L'*H)/(L'*H*L)+(s*s')/(s'*L);  
        d=-H*grad_new;  
        a=(grad_new'*grad_new)/(grad_new'*Q*grad_new);   
        theta_old=theta_new;  
        theta_new = theta_new + a*d;   
 end        
K(1)=Jtheta(500) ;       
    plot(0:99, Jtheta(1:100),'k-o','LineWidth', 4);      
    hold on    
theta_old = zeros(size(x,2),1); %theta的初始值赋值为0        
Jtheta = zeros(itera_num, 1);  
Jtheta(1) = (1/(2*sample_num)).*(x*theta_old-y)'*(x*theta_old-y);    
grad1 = (1/sample_num).*x'*(x*theta_old-y);  
Q=x'*x;  
a=(grad1'*grad1)/(grad1'*Q*grad1);  
H=inv(Q);  
d1=-(H*grad1);  
theta_new=theta_old+a*d1;  
for i = 2:itera_num %计算出某个学习速率alpha下迭代itera_num次数后的参数               
        Jtheta(i) = (1/(2*sample_num)).*(x*theta_new-y)'*(x*theta_new-y);%Jtheta是个行向量        
        grad_old=(1/sample_num).*x'*(x*theta_old-y);    
        grad_new = (1/sample_num).*x'*(x*theta_new-y);   
        L=grad_new-grad_old;  
        s=theta_new-theta_old;  
        H=H-(H*L*s'+s*L'*H)/(L'*s)+(1+(L'*H*L)/(s'*L))*(s*s')/(s'*L);  
        d=-H*grad_new;  
        a=(grad_new'*grad_new)/(grad_new'*Q*grad_new);   
        theta_old=theta_new;  
        theta_new = theta_new + a*d;   
 end        
K(1)=Jtheta(500) ;       
    plot(0:99, Jtheta(1:100),'r-o','LineWidth', 2);      
    hold on    
%%    
legend('CG','BB(1)','BB(2)','Trust Region with DogLeg','0.01','0.03','0.1','0.3','1','1.3','Steepest Descent','NT','DFP','BFGS');        
xlabel('Number of iterations')        
ylabel('Cost function')